augw
Plant augmentation for weighted mixed-sensitivity H∞ and H2 loop-shaping design
Syntax
Description
P = augw(G,W1,W2,W3)P is the
augmented plant of the following diagram.
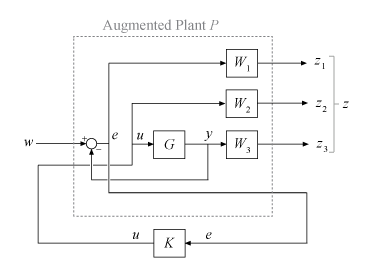
This control structure is used in mixed H∞ synthesis, which lets you design an H∞ controller by simultaneously shaping the frequency responses for tracking and disturbance rejection, noise reduction and robustness, and controller effort. For more information, see Mixed-Sensitivity Loop Shaping.
Examples
Input Arguments
Output Arguments
Tips
For H∞ or H2 synthesis, the models
GandW1,W2,W3must be proper. In other words, they must be bounded as (for continuous-time transfer functions) or (for discrete-time transfer functions). Additionally,W1,W2,W3must be stable. The plantGmust be stabilizable and detectable. Otherwise, the resultingPis not stabilizable by any controller.
Algorithms
augw produces the augmented plant
P(s) given by:
The partitioning is embedded using P = mktito(P,NY,NU), which sets the
P.InputGroup and P.OutputGroup properties as
follows.
[r,c] = size(P);
P.InputGroup = struct('U1',1:c-NU,'U2',c-NU+1:c);
P.OutputGroup = struct('Y1',1:r-NY,'Y2',r-NY+1:r);
Version History
Introduced before R2006a