shnidman
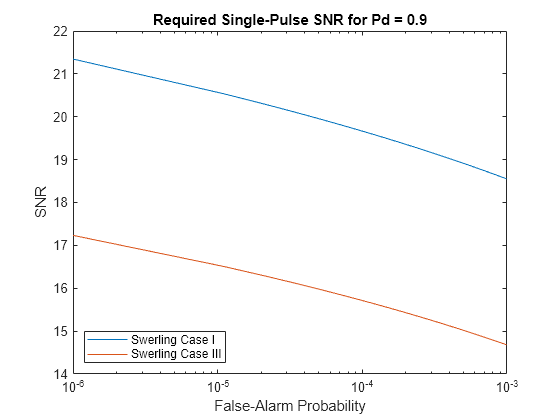
Required SNR using Shnidman’s equation
Description
SNR = shnidman(Pd,Pfa)
Examples
Input Arguments
More About
Extended Capabilities
Version History
Introduced in R2011a