GSC Beamformer
Generalized sidelobe canceller
Libraries:
Phased Array System Toolbox /
Beamforming
Description
The GSC Beamformerblock implements a generalized sidelobe cancellation (GSC) beamformer. A GSC beamformer splits an arrays incoming signals and sends them through a conventional beamformer path and a sidelobe canceling path. The algorithm first presteers the array to the beamforming direction and then adaptively chooses filter weights to minimize power at the output of the sidelobe canceling path. The algorithm uses least mean squares (LMS) to compute the adaptive weights. The final beamformed signal is the difference between the outputs of the two paths.
Ports
Input
Input signal, specified as an M-by-N matrix, where M is the number of samples in the data, and N is the number of array elements.
The size of the first dimension of the input matrix can vary to simulate a changing signal length. A size change can occur, for example, in the case of a pulse waveform with variable pulse repetition frequency.
Data Types: double
Complex Number Support: Yes
Beamforming direction, specified as a 2-by-1 real-valued vector, where
taking the form of [AzimuthAngle;ElevationAngle].
Angle units are in degrees. The azimuth angle must lie between
–180° and 180°, inclusive, and the elevation angle must lie
between –90° and 90°, inclusive. Angles are defined with
respect to the local coordinate system of the array.
Dependencies
To enable this port, set the Source of beamforming
direction parameter to Input port.
Data Types: double
Output
Beamformed output, returned as an M-by-1 complex-valued vector. The quantity M is the number of signal samples.
Parameters
Main Tab
Signal propagation speed, specified as a real-valued positive scalar. The default
value of the speed of light is the value returned by
physconst('LightSpeed'). Units are in meters per second.
Example: 3e8
Data Types: double
Select this parameter to inherit the sample rate from upstream blocks. Otherwise, specify the sample rate using the Sample rate (Hz) parameter.
Data Types: Boolean
Specify the signal sampling rate as a positive scalar. Units are in Hz.
Dependencies
To enable this parameter, clear the Inherit sample rate check box.
Data Types: double
Length of the signal path FIR filter, specified as a positive integer. The FIR filter is a delta function.
The adaptive filter step size factor, specified as a positive scalar. This quantity, when divided by the total power in the sidelobe canceling path, determines the actual adaptive filter step size used by the LMS algorithm.
Beamforming direction, specified as a 2-by-1 real-valued vector taking the form
[AzimuthAngle;ElevationAngle]. Angle units are in degrees. The
azimuth angle must lie between –180° and 180°. The elevation angle must lie
between –90° and 90°. Angles are defined with respect to the local coordinate
system of the array.
Dependencies
To enable this parameter, set the Source of beamforming
direction parameter to Property.
Source of beamforming direction, specified as Property
or Input port. When you set Source of
beamforming direction to Property, you
then set the direction using the Beamforming direction
(deg) parameter. When you select Input
port, the direction is determined by the input to the
Ang port.
Block simulation, specified as Interpreted Execution or
Code Generation. If you want your block to use the
MATLAB® interpreter, choose Interpreted Execution. If
you want your block to run as compiled code, choose Code
Generation. Compiled code requires time to compile but usually runs
faster.
Interpreted execution is useful when you are developing and tuning a model. The block
runs the underlying System object™ in MATLAB. You can change and execute your model quickly. When you are satisfied
with your results, you can then run the block using Code
Generation. Long simulations run faster with generated code than in
interpreted execution. You can run repeated executions without recompiling, but if you
change any block parameters, then the block automatically recompiles before
execution.
This table shows how the Simulate using parameter affects the overall simulation behavior.
When the Simulink® model is in Accelerator mode, the block mode specified
using Simulate using overrides the simulation mode.
Acceleration Modes
| Block Simulation | Simulation Behavior | ||
Normal | Accelerator | Rapid Accelerator | |
Interpreted Execution | The block executes using the MATLAB interpreter. | The block executes using the MATLAB interpreter. | Creates a standalone executable from the model. |
Code Generation | The block is compiled. | All blocks in the model are compiled. | |
For more information, see Choosing a Simulation Mode (Simulink).
Programmatic Use
Block Parameter:
SimulateUsing |
| Type: enum |
Values:
Interpreted Execution, Code
Generation |
Default:
Interpreted Execution |
Sensor Arrays Tab
Method to specify array, specified as Array (no subarrays)
or MATLAB expression.
Array (no subarrays)— use the block parameters to specify the array.MATLAB expression— create the array using a MATLAB expression.
MATLAB expression used to create an array, specified as a valid Phased Array System Toolbox array System object.
Example: phased.URA('Size',[5,3])
Dependencies
To enable this parameter, set Specify sensor array as to
MATLAB expression.
Element Parameters
Antenna or microphone type, specified as one of the following:
Isotropic AntennaCosine AntennaCustom AntennaOmni MicrophoneCustom Microphone
Specify the operating frequency range of the antenna or microphone element as a 1-by-2
row vector in the form [LowerBound,UpperBound]. The element has no
response outside this frequency range. Frequency units are in Hz.
Dependencies
To enable this parameter, set Element type to
Isotropic Antenna, Cosine Antenna, or
Omni Microphone.
Specify the frequencies at which to set antenna and microphone frequency responses as a 1-by-L row vector of increasing real values. The antenna or microphone element has no response outside the frequency range specified by the minimum and maximum elements of this vector. Frequency units are in Hz.
Dependencies
To enable this parameter, set Element type to Custom
Antenna or Custom Microphone. Use
Frequency responses (dB) to set the responses at these
frequencies.
Select this check box to baffle the back response of the element. When back baffled, the responses at all azimuth angles beyond ±90° from broadside are set to zero. The broadside direction is defined as 0° azimuth angle and 0° elevation angle.
Dependencies
To enable this check box, set
Element type to
Isotropic Antenna or
Omni Microphone.
Specify the exponents of the cosine pattern as a nonnegative scalar or a real-valued 1-by-2 matrix of nonnegative values. When Exponent of cosine pattern is a 1-by-2 vector, the first element is the exponent in the azimuth direction and the second element is the exponent in the elevation direction. When you set this parameter to a scalar, both the azimuth direction and elevation direction cosine patterns are raised to the same power.
Dependencies
To enable this parameter, set Element
type to Cosine
Antenna.
Frequency response of a custom antenna or custom microphone for the frequencies defined by the Operating frequency vector (Hz) parameter. The dimensions of Frequency responses (dB) must match the dimensions of the vector specified by the Operating frequency vector (Hz) parameter.
Dependencies
To enable this parameter, set
Element type to
Custom Antenna or
Custom
Microphone.
Coordinate system of custom antenna pattern, specified
az-el or phi-theta. When you
specify az-el, use the Azimuth angles
(deg) and Elevations angles (deg) parameters to
specify the coordinates of the pattern points. When you specify
phi-theta, use the Phi angles (deg)
and Theta angles (deg) parameters to specify the coordinates of the
pattern points.
Dependencies
To enable this parameter, set Element type to
Custom Antenna.
Specify the azimuth angles at which to calculate the antenna radiation pattern as a 1-by-P row vector. P must be greater than 2. Azimuth angles must lie between –180° and 180°, inclusive, and be in strictly increasing order.
Dependencies
To enable this parameter, set the Element type
parameter to Custom Antenna and the
Input Pattern Coordinate System
parameter to az-el.
Specify the elevation angles at which to compute the radiation pattern as a 1-by-Q vector. Q must be greater than 2. Angle units are in degrees. Elevation angles must lie between –90° and 90°, inclusive, and be in strictly increasing order.
Dependencies
To enable this parameter, set the Element type
parameter to Custom Antenna and the
Input Pattern Coordinate System
parameter to az-el.
Phi angles of points at which to specify the antenna radiation pattern, specify as a real-valued 1-by-P row vector. P must be greater than 2. Angle units are in degrees. Phi angles must lie between 0° and 360° and be in strictly increasing order.
Dependencies
To enable this parameter, set the Element type parameter to
Custom Antenna and the Input Pattern Coordinate
System parameter to phi-theta.
Theta angles of points at which to specify the antenna radiation pattern, specify as a real-valued 1-by-Q row vector. Q must be greater than 2. Angle units are in degrees. Theta angles must lie between 0° and 360° and be in strictly increasing order.
Dependencies
To enable this parameter, set the Element type parameter to
Custom Antenna and the Input Pattern Coordinate
System parameter to phi-theta.
Magnitude of the combined antenna radiation pattern, specified as a Q-by-P matrix or a Q-by-P-by-L array.
When the Input Pattern Coordinate System parameter is set to
az-el, Q equals the length of the vector specified by the Elevation angles (deg) parameter and P equals the length of the vector specified by the Azimuth angles (deg) parameter.When the Input Pattern Coordinate System parameter is set to
phi-theta, Q equals the length of the vector specified by the Theta Angles (deg) parameter and P equals the length of the vector specified by the Phi Angles (deg) parameter.
The quantity L equals the length of the Operating frequency vector (Hz).
If this parameter is a Q-by-P matrix, the same pattern is applied to all frequencies specified in the Operating frequency vector (Hz) parameter.
If the value is a Q-by-P-by-L array, each Q-by-P page of the array specifies a pattern for the corresponding frequency specified in the Operating frequency vector (Hz) parameter.
Dependencies
To enable this parameter, set Element type to
Custom Antenna.
Phase of the combined antenna radiation pattern, specified as a Q-by-P matrix or a Q-by-P-by-L array.
When the Input Pattern Coordinate System parameter is set to
az-el, Q equals the length of the vector specified by the Elevation angles (deg) parameter and P equals the length of the vector specified by the Azimuth angles (deg) parameter.When the Input Pattern Coordinate System parameter is set to
phi-theta, Q equals the length of the vector specified by the Theta Angles (deg) parameter and P equals the length of the vector specified by the Phi Angles (deg) parameter.
The quantity L equals the length of the Operating frequency vector (Hz).
If this parameter is a Q-by-P matrix, the same pattern is applied to all frequencies specified in the Operating frequency vector (Hz) parameter.
If the value is a Q-by-P-by-L array, each Q-by-P page of the array specifies a pattern for the corresponding frequency specified in the Operating frequency vector (
Dependencies
To enable this parameter, set Element type to
Custom Antenna.
Select this check box to rotate the antenna element pattern to align with the array normal. When not selected, the element pattern is not rotated.
When the antenna is used in an antenna array and the Input Pattern Coordinate System parameter is az-el, selecting this check box rotates the pattern so that the x-axis of the element coordinate system points along the array normal. Not selecting uses the element pattern without the rotation.
When the antenna is used in an antenna array and Input Pattern Coordinate System is set to phi-theta, selecting this check box rotates the pattern so that the z-axis of the element coordinate system points along the array normal.
Use the parameter in conjunction with the Array normal parameter of the URA and UCA arrays.
Dependencies
To enable this parameter, set Element type to Custom Antenna.
Polar pattern microphone response frequencies, specified as a real scalar, or a real-valued, 1-by-L vector. The response frequencies lie within the frequency range specified by the Operating frequency vector (Hz) vector.
Dependencies
To enable this parameter, set Element type set to
Custom Microphone.
Specify the polar pattern response angles, as a 1-by-P vector. The angles are measured from the central pickup axis of the microphone and must be between –180° and 180°, inclusive.
Dependencies
To enable this parameter, set Element type to
Custom Microphone.
Specify the magnitude of the custom microphone element polar patterns as an L-by-P matrix. L is the number of frequencies specified in Polar pattern frequencies (Hz). P is the number of angles specified in Polar pattern angles (deg). Each row of the matrix represents the magnitude of the polar pattern measured at the corresponding frequency specified in Polar pattern frequencies (Hz) and all angles specified in Polar pattern angles (deg). The pattern is measured in the azimuth plane. In the azimuth plane, the elevation angle is 0° and the central pickup axis is 0° degrees azimuth and 0° degrees elevation. The polar pattern is symmetric around the central axis. You can construct the microphone response pattern in 3-D space from the polar pattern.
Dependencies
To enable this parameter, set Element type to
Custom Microphone.
Array Parameters
Array geometry, specified as one of
ULA— Uniform linear arrayURA— Uniform rectangular arrayUCA— Uniform circular arrayConformal Array— arbitrary element positions
The number of array elements for ULA or UCA arrays, specified as an integer greater than or equal to 2.
Dependencies
To enable this parameter, set Geometry to
ULA or UCA.
Spacing between adjacent array elements:
ULA — specify the spacing between two adjacent elements in the array as a positive scalar.
URA — specify the spacing as a positive scalar or a 1-by-2 vector of positive values. If Element spacing (m) is a scalar, the row and column spacings are equal. If Element spacing (m) is a vector, the vector has the form
[SpacingBetweenArrayRows,SpacingBetweenArrayColumns].
Dependencies
To enable this parameter, set Geometry to
ULA or URA.
Linear axis direction of ULA, specified as y,
x, or z. All ULA array
elements are uniformly spaced along this axis in the local array coordinate
system.
Dependencies
To enable this parameter, set Geometry to
ULA.This parameter is also enabled when the block only supports ULA arrays.
Dimensions of a URA array, specified as a positive integer or 1-by-2 vector of positive integers.
If Array size is a 1-by-2 vector, the vector has the form
[NumberOfArrayRows,NumberOfArrayColumns].If Array size is an integer, the array has the same number of elements in each row and column.
For a URA, array elements are indexed from top to bottom along the
leftmost array column, and continued to the next columns from left to right. In this
figure, the Array size value of [3,2] creates an
array having three rows and two columns.
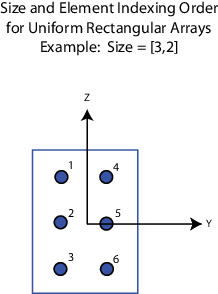
Dependencies
To enable this parameter, set Geometry to
URA.
Lattice of URA element positions, specified as Rectangular
or Triangular.
Rectangular— Aligns all the elements in row and column directions.Triangular— Shifts the even-row elements of a rectangular lattice toward the positive row-axis direction. The displacement is one-half the element spacing along the row dimension.
Dependencies
To enable this parameter, set Geometry to
URA.
Array normal direction, specified as
x,
y, or
z.
Elements of planar arrays lie in a plane orthogonal to the selected array normal direction. Element boresight directions point along the array normal direction.
| Array Normal Parameter Value | Element Positions and Boresight Directions |
|---|---|
x | Array elements lie in the yz-plane. All element boresight vectors point along the x-axis. |
y | Array elements lie in the zx-plane. All element boresight vectors point along the y-axis. |
z | Array elements lie in the xy-plane. All element boresight vectors point along the z-axis. |
Dependencies
To enable this parameter, set
Geometry to
URA or
UCA.
Radius of UCA array, specified as a positive scalar.
Dependencies
To enable this parameter, set Geometry to
UCA.
Positions of the elements in a conformal array, specified as a
3-by-N matrix of real values, where N is the
number of elements in the conformal array. Each column of this matrix represents the
position [x;y;z]of an array element in the array local coordinate
system. The origin of the local coordinate system is (0,0,0). Units
are in meters.
Dependencies
To enable this parameter set Geometry to Conformal
Array.
Data Types: double
Direction of element normal vectors in a conformal array, specified as a 2-by-1 column
vector or a 2-by-N matrix. N indicates the number
of elements in the array. If the parameter value is a matrix, each column specifies the
normal direction of the corresponding element in the form
[azimuth;elevation] with respect to the local coordinate system.
The local coordinate system aligns the positive x-axis with the
direction normal to the conformal array. If the parameter value is a 2-by-1 column
vector, the same pointing direction is used for all array elements.
You can use the Element positions (m) and Element normals (deg) parameters to represent any arrangement in which pairs of elements differ by certain transformations. The transformations can combine translation, azimuth rotation, and elevation rotation. However, you cannot use transformations that require rotation about the normal direction.
To enable this parameter, set Geometry to Conformal
Array.
Data Types: double
Specify element tapering as a complex-valued scalar or a complex-valued 1-by-N row vector. In this vector, N represents the number of elements in the array.
Also known as element weights, tapers multiply the array element responses. Tapers modify both amplitude and phase of the response to reduce side lobes or steer the main response axis.
If Taper is a scalar, the same weight is applied to each element. If Taper is a vector, a weight from the vector is applied to the corresponding sensor element. The number of weights must match the number of elements of the array.
Data Types: double
More About
The generalized sidelobe canceller (GSC) is an efficient implementation of a linear constraint minimum variance (LCMV) beamformer. LCMV beamforming minimizes the output power of an array while preserving the power in one or more specified directions. This type of beamformer is called a constrained beamformer. You can compute exact weights for the constrained beamformer but the computation is costly when the number of elements is large. The computation requires the inversion of a large spatial covariance matrix. The GSC formulation converts the adaptive constrained optimization LCMV problem into an adaptive unconstrained problem, which simplifies the implementation.
In the GSC algorithm, incoming sensor data is split into two signal paths as shown in the block diagram. The upper path is a conventional beamformer. The lower path is an adaptive unconstrained beamformer whose purpose is to minimize the GSC output power. The GSC algorithm consists of these steps:
Presteer the element sensor data by time-shifting the incoming signals. Presteering time-aligns all sensor element signals. The time shifts depend on the arrival angle of the signal.
Pass the presteered signals through the upper path into a conventional beamformer with fixed weights, wconv.
Also pass the presteered signals through the lower path into the blocking matrix, B. The blocking matrix is orthogonal to the signal and removes the signal from the lower path.
Filter the lower path signals through a bank of FIR filters. The
FilterLengthproperty sets the length of the filters. The filter coefficients are the adaptive filter weights, wad.Compute the difference between the upper and lower signal paths. This difference is the beamformed GSC output.
Feed the beamformed output back into the filter. Adapt the filter weights using a least mean-square (LMS) algorithm. The adaptive LMS step size is the quantity set by the
LMSStepSizeFactorproperty, divided by the total signal power.

Version History
Introduced in R2016b
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)