structuralIC

Set initial conditions for a transient structural model

Domain-specific structural workflow is not recommended. New features might not be compatible with this workflow. For help migrating your existing code to the unified finite element workflow, see Migration from Domain-Specific to Unified Workflow.

Syntax

structuralIC(structuralmodel,"Displacement",u0,"Velocity",v0)

structuralIC(___RegionType,RegionID)

structuralIC(structuralmodel,Sresults)

structuralIC(structuralmodel,Sresults,iT)

struct_ic = structuralIC(___)

Description

structuralIC(structuralmodel,"Displacement",u0,"Velocity",v0) sets initial displacement and velocity for the entire geometry.

structuralIC(___RegionType,RegionID) sets initial displacement and velocity for a particular geometry region using the arguments from the previous syntax.

structuralIC(structuralmodel,Sresults) sets initial displacement and velocity using the solution Sresults from a previous structural analysis on the same geometry. If Sresults is obtained by solving a transient structural problem, then structuralIC uses the solution Sresults for the last time-step.

structuralIC(structuralmodel,Sresults,iT) uses the solution Sresults for the time-step iT from a previous structural analysis on the same geometry.

struct_ic = structuralIC(___) returns a handle to the structural initial conditions object.

Examples

Specify Initial Velocity

Specify initial velocity values for the entire geometry and for a particular face.

Create a transient dynamic model for a 3-D problem.

structuralmodel = createpde("structural","transient-solid");

Create a geometry and include it into the model. Plot the geometry.

gm = multicuboid(0.06,0.005,0.01);
structuralmodel.Geometry = gm;
pdegplot(structuralmodel,"FaceLabels","on","FaceAlpha",0.5)
view(50,20)

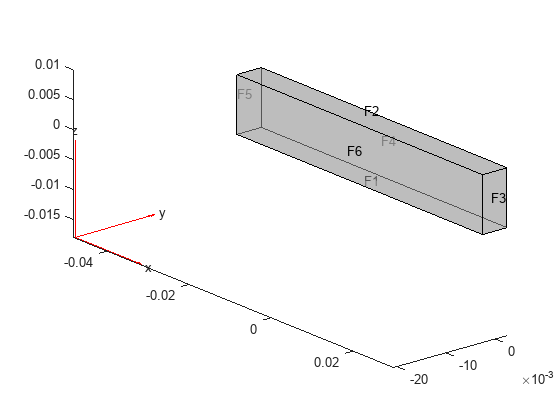
Specify the zero initial velocity on the entire geometry. When you specify only the initial velocity or initial displacement, structuralIC assumes that the omitted parameter is zero. For example, here the initial displacement is also zero.

structuralIC(structuralmodel,"Velocity",[0;0;0])

ans = 
  GeometricStructuralICs with properties:

             RegionType: 'Cell'
               RegionID: 1
    InitialDisplacement: []
        InitialVelocity: [3x1 double]

Update the initial velocity on face 2 to model impulsive excitation.

structuralIC(structuralmodel,"Face",2,"Velocity",[0;60;0])

ans = 
  GeometricStructuralICs with properties:

             RegionType: 'Face'
               RegionID: 2
    InitialDisplacement: []
        InitialVelocity: [3x1 double]

Specify Nonconstant Initial Displacement by Using Function Handle

Specify initial z-displacement to be dependent on the coordinates x and y.

Create a transient dynamic model for a 3-D problem.

structuralmodel = createpde("structural","transient-solid");

Create the geometry and include it into the model. Plot the geometry.

gm = multicuboid(0.06,0.005,0.01);
structuralmodel.Geometry = gm;
pdegplot(structuralmodel,"FaceLabels","on","FaceAlpha",0.5)
view(50,20)

Specify the zero initial displacement on the entire geometry.

structuralIC(structuralmodel,"Displacement",[0;0;0])

ans = 
  GeometricStructuralICs with properties:

             RegionType: 'Cell'
               RegionID: 1
    InitialDisplacement: [3x1 double]
        InitialVelocity: []

Now change the initial displacement in the z-direction on face 2 to a function of the coordinates x and y:

$$\mathit{u}\left(0\right)=\left[\begin{array}{c}0\\ 0\\ {\mathit{x}}^2+{\mathit{y}}^2\end{array}\right]$$

Write the following function file. Save it to a location on your MATLAB® path.

function uinit = initdisp(location)

M = length(location.x);

uinit = zeros(3,M);

uinit(3,:) = location.x.^2 + location.y.^2;

Pass the initial displacement to your structural model.

structuralIC(structuralmodel,"Face",2,"Displacement",@initdisp)

ans = 
  GeometricStructuralICs with properties:

             RegionType: 'Face'
               RegionID: 2
    InitialDisplacement: @initdisp
        InitialVelocity: []

Use Static Solution as Initial Condition

Use a static solution as an initial condition for a dynamic structural model.

Create a static model.

staticmodel = createpde("structural","static-solid");

Create the geometry and include it in the model. Plot the geometry.

gm = multicuboid(0.06,0.005,0.01);
staticmodel.Geometry = gm;
pdegplot(staticmodel,"FaceLabels","on","FaceAlpha",0.5)
view(50,20)

Specify Young's modulus, Poisson's ratio, and the mass density.

structuralProperties(staticmodel,"YoungsModulus",210E9, ...
                                 "PoissonsRatio",0.3,...
                                 "MassDensity",7800);

Apply the boundary condition and static load.

structuralBC(staticmodel,"Face",5,"Constraint","fixed");
structuralBoundaryLoad(staticmodel,"Face",3, ...
                                   "SurfaceTraction", ...
                                   [0;1E6;0]);

Generate a mesh and solve the model.

generateMesh(staticmodel,"Hmax",0.02);
Rstatic = solve(staticmodel);

Create a dynamic model and assign geometry.

dynamicmodel = createpde("structural","transient-solid");
gm = multicuboid(0.06,0.005,0.01);
dynamicmodel.Geometry = gm;

Apply the boundary condition.

structuralBC(dynamicmodel,"Face",5,"Constraint","fixed");

Generate a mesh.

generateMesh(dynamicmodel,"Hmax",0.02);

Specify the initial condition using the static solution.

structuralIC(dynamicmodel,Rstatic)

ans = 
  NodalStructuralICs with properties:

    InitialDisplacement: [189x3 double]
        InitialVelocity: [189x3 double]

Input Arguments

structuralmodel — Transient structural model

StructuralModel object

Transient structural model, specified as a StructuralModel object. The model contains the geometry, mesh, structural properties of the material, body loads, boundary loads, boundary conditions, and initial conditions.

Example: structuralmodel = createpde("structural","transient-solid")

u0 — Initial displacement

numeric vector | function handle

Initial displacement, specified as a numeric vector or function handle. A numeric vector must contain two elements for a 2-D model and three elements for a 3-D model. The elements represent the components of initial displacement.

Use a function handle to specify spatially varying initial displacement. The function must return a two-row matrix for a 2-D model and a three-row matrix for a 3-D model. Each column of the matrix corresponds to the initial displacement at the coordinates provided by the solver. For details, see More About.

Example: structuralIC(structuralmodel,"Face",[2,5],"Displacement",[0;0;0.01])

Data Types: double | function_handle

v0 — Initial velocity

numeric vector | function handle

Initial velocity, specified as a numeric vector or function handle. A numeric vector must contain two elements for a 2-D model and three elements for a 3-D model. The elements represent the components of initial velocity.

Use a function handle to specify spatially varying initial velocity. The function must return a two-row matrix for a 2-D model and a three-row matrix for a 3-D model. Each column of the matrix corresponds to the initial velocity at the coordinates provided by the solver. For details, see More About.

Example: structuralIC(structuralmodel,"Face",[2,5],"Displacement",[0;0;0.01],"Velocity",[0;60;0])

Data Types: double | function_handle

RegionType — Geometric region type

"Face" | "Edge" | "Vertex" | "Cell"

Geometric region type, specified as "Face", "Edge", "Vertex", or "Cell".

When you apply multiple initial condition assignments, the solver uses these precedence rules for determining the initial condition.

• For multiple assignments to the same geometric region, the solver uses the last applied setting.

• For separate assignments to a geometric region and the boundaries of that region, the solver uses the specified assignment on the region and chooses the assignment on the boundary as follows. The solver gives an "Edge" assignment precedence over a "Face" assignment, even if you specify a "Face" assignment after an "Edge" assignment. The precedence levels are "Vertex" (highest precedence), "Edge", "Face", "Cell" (lowest precedence).

• For an assignment made with the results object, the solver uses that assignment instead of all previous assignments.

Example: structuralIC(structuralmodel,"Face",[2,5],"Displacement",[0;0;0.01],"Velocity",[0;60;0])

Data Types: char

RegionID — Geometric region ID

vector of positive integers

Geometric region ID, specified as a vector of positive integers. Find the region IDs by using pdegplot.

Example: structuralIC(structuralmodel,"Face",[2,5],"Displacement",[0;0;0.01],"Velocity",[0;60;0])

Data Types: double

Sresults — Structural model solution

StaticStructuralResults object | TransientStructuralResults object

Structural model solution, specified as a StaticStructuralResults or TransientStructuralResults object. Create Sresults by using solve.

iT — Time index

positive integer

Time index, specified as a positive integer.

Example: structuralIC(structuralmodel,Sresults,21)

Data Types: double

Output Arguments

struct_ic — Handle to initial conditions

GeometricStructuralICs object | NodalStructuralICs object

Handle to initial conditions, returned as a GeometricStructuralICs or NodalStructuralICs object. See GeometricStructuralICs Properties and NodalStructuralICs Properties.

structuralIC associates the structural initial condition with the geometric region in the case of a geometric assignment, or the nodes in the case of a results-based assignment.

More About

Specifying Nonconstant Parameters of a Structural Model

Use a function handle to specify the following structural parameters when they depend on space and, depending of the type of structural analysis, either time or frequency:

• Surface traction on the boundary

• Pressure normal to the boundary

• Concentrated force at a vertex

• Distributed spring stiffness for each translational direction used to model elastic foundation

• Enforced displacement and its components

• Initial displacement and velocity (can depend on space only)

For example, use function handles to specify the pressure load, x-component of the enforced displacement, and the initial displacement for this model.

structuralBoundaryLoad(model,"Face",12, ...
                             "Pressure",@myfunPressure)
structuralBC(model,"Face",2, ...
                   "XDisplacement",@myfunBC)
structuralIC(model,"Face",12, ...
                   "Displacement",@myfunIC)

For all parameters, except the initial displacement and velocity, the function must be of the form:

function structuralVal = myfun(location,state)

For the initial displacement and velocity the function must be of the form:

function structuralVal = myfun(location)

The solver computes and populates the data in the location and state structure arrays and passes this data to your function. You can define your function so that its output depends on this data. You can use any names instead of location and state, but the function must have exactly two arguments (or one argument if the function specifies the initial displacement or initial velocity).

• location — A structure containing these fields:

  • location.x — The x-coordinate of the point or points

  • location.y — The y-coordinate of the point or points

  • location.z — For a 3-D or an axisymmetric geometry, the z-coordinate of the point or points

  • location.r — For an axisymmetric geometry, the r-coordinate of the point or points

  Furthermore, for boundary conditions, the solver passes these data in the location structure:

  • location.nx — x-component of the normal vector at the evaluation point or points

  • location.ny — y-component of the normal vector at the evaluation point or points

  • location.nz — For a 3-D or an axisymmetric geometry, z-component of the normal vector at the evaluation point or points

  • location.nr — For an axisymmetric geometry, r-component of the normal vector at the evaluation point or points

• state — A structure containing these fields for dynamic structural problems:

  • state.time contains the time at evaluation points.

  • state.frequency contains the frequency at evaluation points.

  state.time and state.frequency are scalars.

Boundary constraints and loads get these data from the solver:

• location.x, location.y, location.z, location.r

• location.nx, location.ny, location.nz, location.nr

• state.time or state.frequency (depending of the type of structural analysis)

Initial conditions get these data from the solver:

• location.x, location.y, location.z, location.r

• Subdomain ID

If a parameter represents a vector value, such as surface traction, spring stiffness, force, or displacement, your function must return a two-row matrix for a 2-D model and a three-row matrix for a 3-D model. Each column of the matrix corresponds to the parameter value (a vector) at the boundary coordinates provided by the solver.

If a parameter represents a scalar value, such as pressure or a displacement component, your function must return a row vector where each element corresponds to the parameter value (a scalar) at the boundary coordinates provided by the solver.

If boundary conditions depend on state.time or state.frequency, ensure that your function returns a matrix of NaN of the correct size when state.frequency or state.time are NaN. Solvers check whether a problem is nonlinear or time dependent by passing NaN state values and looking for returned NaN values.

Additional Arguments in Functions for Nonconstant Structural Parameters

To use additional arguments in your function, wrap your function (that takes additional arguments) with an anonymous function that takes only the location and state arguments. For example:

structuralVal = ...
@(location,state) myfunWithAdditionalArgs(location,state,arg1,arg2...)
structuralBC(model,"Face",2,"XDisplacement",structuralVal)

structuralVal = ...
@(location) myfunWithAdditionalArgs(location,arg1,arg2...)
structuralIC(model,"Face",2,"Displacement",structuralVal)

Version History

Introduced in R2018a