interpolateMagneticPotential
Interpolate magnetic potential in magnetostatic result at arbitrary spatial locations
Since R2021a
Syntax
Description
Aintrp = interpolateMagneticPotential(magnetostaticresults,xq,yq)xq and yq.
Aintrp = interpolateMagneticPotential(magnetostaticresults,xq,yq,zq)xq, yq, and
zq.
Aintrp = interpolateMagneticPotential(magnetostaticresults,querypoints)querypoints.
Examples
Create a square geometry and plot it with the edge labels.
R1 = [3,4,-1,1,1,-1,1,1,-1,-1]'; g = decsg(R1,'R1',('R1')'); pdegplot(g,EdgeLabels="on") xlim([-1.1 1.1]) ylim([-1.1 1.1])

Create an femodel object for magnetostatic analysis and include the geometry into the model.
model = femodel(AnalysisType="magnetostatic", ... Geometry=g);
Specify the vacuum permeability in the SI system of units.
model.VacuumPermeability = 1.2566370614E-6;
Specify the relative permeability of the material.
model.MaterialProperties = ...
materialProperties(RelativePermeability=5000);Apply the magnetic potential boundary conditions on the boundaries of the square.
model.EdgeBC([1 3]) = edgeBC(MagneticPotential=0); model.EdgeBC([2 4]) = edgeBC(MagneticPotential=0.01);
Specify the current density for the entire geometry.
model.FaceLoad = faceLoad(CurrentDensity=0.5);
Generate the mesh.
model = generateMesh(model);
Solve the problem and plot the magnetic potential.
R = solve(model); pdeplot(R.Mesh,XYData=R.MagneticPotential, ... Contour="on") axis equal
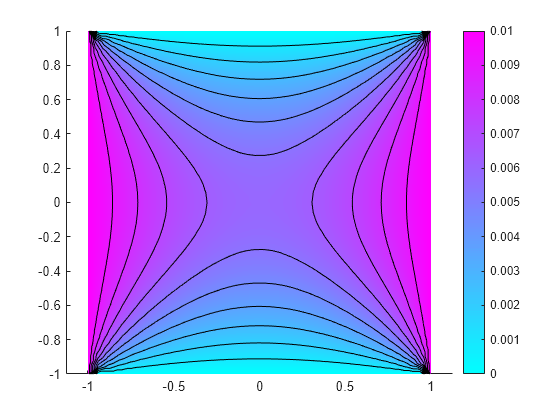
Interpolate the resulting magnetic potential to a grid covering the central portion of the geometry, for x and y from -0.5 to 0.5.
v = linspace(-0.5,0.5,51); [X,Y] = meshgrid(v); Aintrp = interpolateMagneticPotential(R,X,Y);
Reshape Aintrp and plot the resulting magnetic potential.
Aintrp = reshape(Aintrp,size(X));
figure
contourf(X,Y,Aintrp)
colormap(cool)
colorbar
axis equal
Alternatively, you can specify the grid by using a matrix of query points.
querypoints = [X(:),Y(:)]'; Aintrp = interpolateMagneticPotential(R,querypoints);
Create an femodel object for magnetostatic analysis and include a geometry of a plate with a hole into the model.
model = femodel(AnalysisType="magnetostatic", ... Geometry="PlateHoleSolid.stl");
Plot the geometry.
pdegplot(model.Geometry,FaceLabels="on",FaceAlpha=0.3)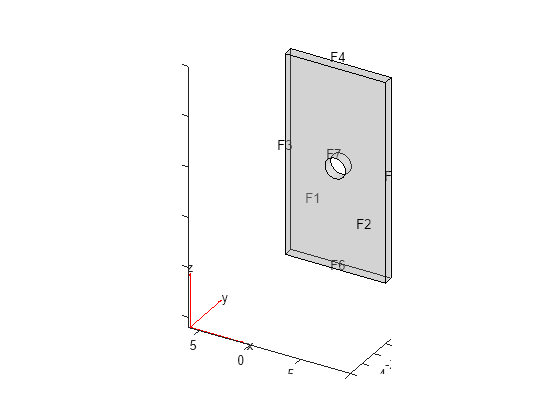
Specify the vacuum permeability value in the SI system of units.
model.VacuumPermeability = 1.2566370614E-6;
Specify the relative permeability of the material.
model.MaterialProperties = ...
materialProperties(RelativePermeability=5000);Specify the current density for the entire geometry.
model.CellLoad = cellLoad(CurrentDensity=[0;0;0.5]);
Apply the magnetic potential boundary conditions on the side faces and the face bordering the hole.
model.FaceBC(3:6) = faceBC(MagneticPotential=[0;0;0]); model.FaceBC(7) = faceBC(MagneticPotential=[0;0;0.01]);
Generate the linear mesh.
model = generateMesh(model);
Solve the problem.
R = solve(model)
R =
MagnetostaticResults with properties:
MagneticPotential: [1×1 FEStruct]
MagneticField: [1×1 FEStruct]
MagneticFluxDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
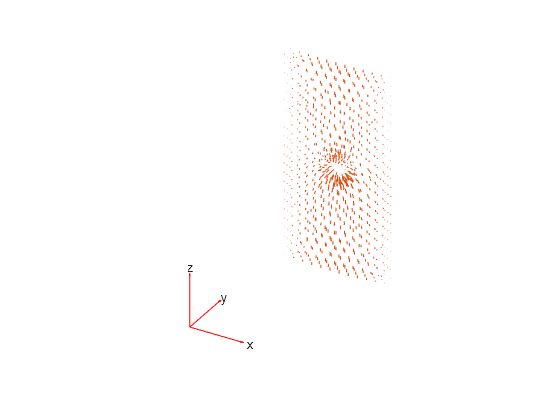
Plot the magnetic potential.
pdeplot3D(R.Mesh,FlowData=[R.MagneticPotential.Ax ... R.MagneticPotential.Ay ... R.MagneticPotential.Az])
Interpolate the resulting magnetic potential to a grid covering the entire geometry, for x, y, and z.
x = linspace(0,10,11); y = linspace(0,1,5); z = linspace(0,20,11); [X,Y,Z] = meshgrid(x,y,z); Aintrp = interpolateMagneticPotential(R,X,Y,Z);
Reshape Aintrp.Ax, Aintrp.Ay, and Aintrp.Az to match the shape of the input grid.
AintrpX = reshape(Aintrp.Ax,size(X)); AintrpY = reshape(Aintrp.Ay,size(Y)); AintrpZ = reshape(Aintrp.Az,size(Z));
Plot the resulting magnetic potential.
figure
quiver3(X,Y,Z,AintrpX,AintrpY,AintrpZ,Color="red")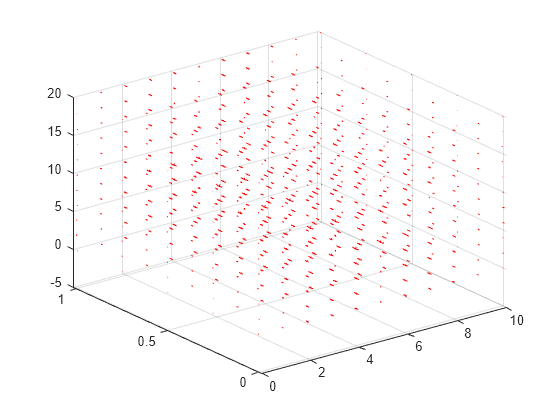
Input Arguments
Solution of a magnetostatic problem, specified as a MagnetostaticResults object. Create magnetostaticresults
using the solve function.
x-coordinate query points, specified as a real array.
interpolateMagneticPotential evaluates the magnetic potential at
the 2-D coordinate points [xq(i) yq(i)] or at the 3-D coordinate
points [xq(i) yq(i) zq(i)] for every i. Because of
this, xq, yq, and (if present)
zq must have the same number of entries.
interpolateMagneticPotential converts query points to column
vectors xq(:), yq(:), and (if present)
zq(:). It returns magnetic potential values as a column vector of
the same size. To ensure that the dimensions of the returned solution are consistent
with the dimensions of the original query points, use reshape. For
example, use Aintrp = reshape(Aintrp,size(xq)).
Example: xq = [0.5 0.5 0.75 0.75]
Data Types: double
y-coordinate query points, specified as a real array.
interpolateMagneticPotential evaluates the magnetic potential at
the coordinate points [xq(i),yq(i)] for every i.
Because of this, xq and yq must have the same
number of entries.
interpolateMagneticPotential converts query points to column
vectors xq(:), yq(:), and (if present)
zq(:). It returns magnetic potential values as a column vector of
the same size. To ensure that the dimensions of the returned solution are consistent
with the dimensions of the original query points, use reshape. For
example, use Aintrp = reshape(Aintrp,size(yq)).
Example: yq = [1 2 0 0.5]
Data Types: double
z-coordinate query points, specified as a real array.
interpolateMagneticPotential evaluates the magnetic potential at
the 3-D coordinate points [xq(i) yq(i) zq(i)]. Therefore,
xq, yq, and zq must have
the same number of entries.
interpolateMagneticPotential converts the query points to column
vectors xq(:), yq(:), and
zq(:). It returns magnetic potential values as a column vector of the
same size. To ensure that the dimensions of the returned solution are consistent with
the dimensions of the original query points, use reshape. For
example, use Aintrp = reshape(Aintrp,size(zq)).
Example: zq = [1 1 0 1.5]
Data Types: double
Query points, specified as a real matrix with either two rows for 2-D geometry or
three rows for 3-D geometry. interpolateMagneticPotential evaluates
the magnetic potential at the coordinate points querypoints(:,i) for
every i, so each column of querypoints contains
exactly one 2-D or 3-D query point.
Example: For a 2-D geometry, querypoints = [0.5 0.5 0.75 0.75; 1 2 0
0.5]
Data Types: double
Output Arguments
Magnetic potential at query points, returned as a vector for a 2-D problem or an
FEStruct object for a 3-D problem. The properties of
FEStruct contain the components of the magnetic potential at query
points. For query points i that are outside the geometry,
Aintrp(i), Aintrp.Ax(i),
Aintrp.Ay(i), and Aintrp.Az(i) are
NaN. Properties of an FEStruct object are
read-only.
Version History
Introduced in R2021a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)