Cuboids, Cylinders, and Spheres

This example shows how to create 3-D geometries formed by one or more cubic, cylindrical, and spherical cells by using the multicuboid, multicylinder, and multisphere functions, respectively. With these functions, you can create stacked or nested geometries. You also can create geometries where some cells are empty; for example, hollow cylinders, cubes, or spheres.

All cells in a geometry must be of the same type: either cuboids, or cylinders, or spheres. These functions do not combine cells of different types in one geometry.

Single Sphere

Create a geometry that consists of a single sphere and include this geometry in a PDE model.

Use the multisphere function to create a single sphere. The resulting geometry consists of one cell.

gm = multisphere(5)

gm = 
  DiscreteGeometry with properties:

       NumCells: 1
       NumFaces: 1
       NumEdges: 0
    NumVertices: 0
       Vertices: []

Create a PDE model.

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Include the geometry in the model.

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Plot the geometry.

pdegplot(model,"CellLabels","on")

Nested Cuboids of Same Height

Create a geometry that consists of three nested cuboids of the same height and include this geometry in a PDE model.

Create the geometry by using the multicuboid function. The resulting geometry consists of three cells.

gm = multicuboid([2 3 5],[4 6 10],3)

gm = 
  DiscreteGeometry with properties:

       NumCells: 3
       NumFaces: 18
       NumEdges: 36
    NumVertices: 24
       Vertices: [24x3 double]

Create a PDE model.

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Include the geometry in the model.

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Plot the geometry.

pdegplot(model,"CellLabels","on","FaceAlpha",0.5)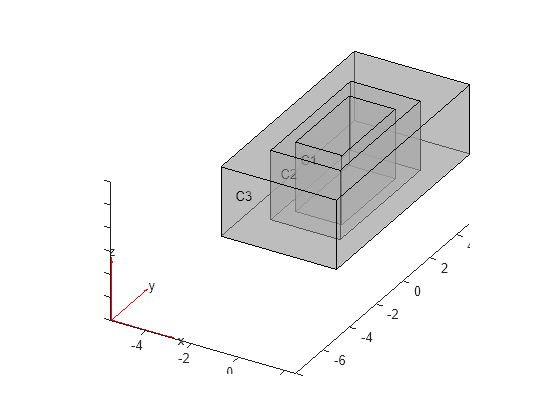

Stacked Cylinders

Create a geometry that consists of three stacked cylinders and include this geometry in a PDE model.

Create the geometry by using the multicylinder function with the ZOffset argument. The resulting geometry consists of four cells stacked on top of each other.

gm = multicylinder(10,[1 2 3 4],"ZOffset",[0 1 3 6])

gm = 
  DiscreteGeometry with properties:

       NumCells: 4
       NumFaces: 9
       NumEdges: 5
    NumVertices: 5
       Vertices: [5x3 double]

Create a PDE model.

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Include the geometry in the model.

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Plot the geometry.

pdegplot(model,"CellLabels","on","FaceAlpha",0.5)

Hollow Cylinder

Create a hollow cylinder and include it as a geometry in a PDE model.

Create a hollow cylinder by using the multicylinder function with the Void argument. The resulting geometry consists of one cell.

gm = multicylinder([9 10],10,"Void",[true,false])

gm = 
  DiscreteGeometry with properties:

       NumCells: 1
       NumFaces: 4
       NumEdges: 4
    NumVertices: 4
       Vertices: [4x3 double]

Create a PDE model.

model = createpde

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Include the geometry in the model.

model.Geometry = gm

model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Plot the geometry.

pdegplot(model,"CellLabels","on","FaceAlpha",0.5)

×

Open Example

You have a modified version of this example. Do you want to open this example with your edits?

No, overwrite the modified version Yes