Choose Between spmd, parfor, and parfeval

Choose Between `spmd`, `parfor`, and `parfeval`

To run computations in parallel, you can use spmd, parfor, parfeval, or parfevalOnAll. Each construct relies on different parallel programming concepts.

When to Use `parfor`

A parfor-loop can be useful if you have a for-loop with slow loop iterations or many loop iterations. Each iteration must be independent of all others. For more help in deciding when to use parfor, see Decide When to Use parfor.

When to Use `spmd`

Run Communicating Parallel Code

Use spmd if you require fine-grained worker-to-worker communication and collaboration between workers during a computation. parfor, parfeval, and parfevalOnAll do not allow communication between workers. Computations with spmd can involve communication between workers using the spmdSend, spmdReceive, and spmdSendReceive functions.

If you are unsure, ask yourself the following: within my parallel code, can each computation be completed without any communication between workers? If yes, use parfor or parfeval. Otherwise, use spmd.

Run Parallel and Customized Code on Distributed Arrays

Use spmd if your computations involve large arrays distributed across workers. You can perform simultaneous calculations on all workers or perform customized calculations on specific workers.

When workers run an spmd block, each worker is assigned a unique index, the spmdIndex. This lets you specify code to be run only on certain workers, and target sections of distributed arrays.

Synchronous and Asynchronous Work

When choosing between parfor, parfeval, and spmd, consider whether your calculation requires synchronization with the client.

parfor and spmd require synchronization, and therefore block you from running any new computations on the MATLAB^® client. parfeval does not require synchronization, so you can continue to use the client.

Use Other Functional Capabilities

spmd and parfeval have other capabilities you can use after you have submitted your computations.

With spmd, you can collect results computed inside the spmd statement without transferring the results to the client. Access the values of the variables assigned inside the spmd statement as Composite objects from the client. For more information, see Access Worker Variables with Composites.
When you submit a parfeval task, MATLAB schedules the task to run asynchronously and returns Future objects before the submitted task finishes running. A Future object represents the task that MATLAB has scheduled. You can interact with Future objects in different ways:
- Use fetchNext to retrieve results as they become available or check if results are ready.
- Stop parfeval calculations from running using the cancel function.
- Use Future objects in other computation on the client.

Compare Performance of `parfor`, `parfeval`, and `spmd`

Open Live Script

Using spmd can be slower or faster than using parfor-loops or parfeval, depending on the type of computation. Overhead affects the relative performance of parfor-loops, parfeval, and spmd.

For a set of tasks, parfor and parfeval typically perform better than spmd under these conditions:

The computational time taken per task is not deterministic.
The computational time taken per task is not uniform.
The data returned from each task is small.

Use parfeval when:

You want to run computations in the background.
Each task is dependent on other tasks.

In this example, you examine the speed at which the software performs matrix operations when using a parfor-loop, parfeval, and spmd.

First, create a parallel pool of process workers p.

p = parpool("Processes");

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 6 workers.

Compute Random Matrices

Examine the speed at which the software can generate random matrices by using a parfor-loop, parfeval, and spmd. Set the number of trials (n) and the matrix size (for an m-by-m matrix). Increasing the number of trials improves the statistics used in later analysis, but does not affect the calculation itself.

m = 1500;
n = 20;

Then, use a parfor-loop to execute rand(m) once for each worker. Time each of the n trials.

parforTime = zeros(n,1);
for i = 1:n
    tic;
    mats = cell(1,p.NumWorkers);
    parfor N = 1:p.NumWorkers
      mats{N} = rand(m);
    end
    parforTime(i) = toc;
end

Next, use parfeval to execute rand(m) once for each worker. Time each of the n trials.

parfevalTime = zeros(n,1);
for i = 1:n
    tic;
    f(1:p.NumWorkers) = parallel.FevalFuture;
    for N = 1:p.NumWorkers
      f(N) = parfeval(@rand,1,m);
    end
    mats = fetchOutputs(f);
    parfevalTime(i) = toc;
    clear f
end

Finally, use spmd to execute rand(m) once for each worker. You can use spmdCat to concatenate the values of mat on each worker into array mats and store it on worker 1. For details on workers and how to execute commands on them with spmd, see Run Single Programs on Multiple Data Sets. Time each of the n trials.

spmdTime = zeros(n,1);
for i = 1:n
    tic;
    spmd
        mat = rand(m);
        mats = spmdCat({mat}, 1, 1);
    end
    allMats = mats{1};
    spmdTime(i) = toc;
end

Use rmoutliers to remove the outliers from each of the trials. Then, use boxplot to compare the times.

% Hide outliers
boxData = rmoutliers([parforTime parfevalTime spmdTime]);

% Plot data
boxplot(boxData, 'labels',{'parfor','parfeval','spmd'}, 'Symbol','')
ylabel('Time (seconds)')
title('Make n Random Matrices (m-by-m)')

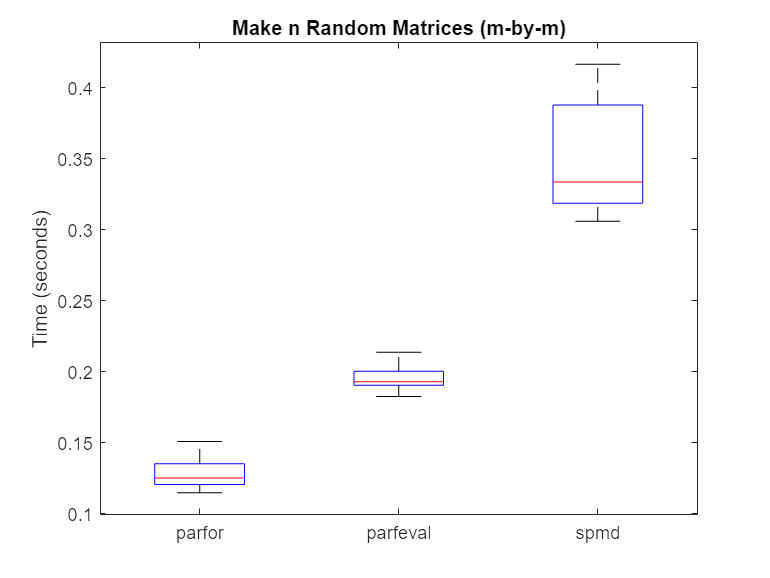
Typically, spmd requires more overhead per evaluation than parfor or parfeval. Therefore, in this case, using a parfor-loop or parfeval is more efficient.

Compute Sum of Random Matrices

Next, compute the sum of random matrices. You can do this by using a reduction variable with a parfor-loop, a sum after computations with parfeval, or spmdPlus with spmd. Again, set the number of trials (n) and the matrix size (for an m-by-m matrix).

m = 1500;
n = 20;

Then, use a parfor-loop to execute rand(m) once for each worker. Compute the sum with a reduction variable. Time each of the n trials.

parforTime = zeros(n,1);
for i = 1:n
    tic;
    result = 0;
    parfor N = 1:p.NumWorkers
      result = result + rand(m);
    end
    parforTime(i) = toc;
end

Next, use parfeval to execute rand(m) once for each worker. Use fetchOutputs to fetch all of the matrices, then use sum. Time each of the n trials.

parfevalTime = zeros(n,1);
for i = 1:n
    tic;
    f(1:p.NumWorkers) = parallel.FevalFuture;
    for N = 1:p.NumWorkers
      f(N) = parfeval(@rand,1,m);
    end
    result = sum(fetchOutputs(f));
    parfevalTime(i) = toc;
    clear f
end

Finally, use spmd to execute rand(m) once for each worker. Use spmdPlus to sum all of the matrices. To send the result only to the first worker, set the optional target worker argument to 1. Time each of the n trials.

spmdTime = zeros(n,1);
for i = 1:n
    tic;
    spmd
        r = spmdPlus(rand(m), 1);
    end
    result = r{1};
    spmdTime(i) = toc;
end

Use rmoutliers to remove the outliers from each of the trials. Then, use boxplot to compare the times.

% Hide outliers
boxData = rmoutliers([parforTime parfevalTime spmdTime]);

% Plot data
boxplot(boxData, 'labels',{'parfor','parfeval','spmd'}, 'Symbol','')
ylabel('Time (seconds)')
title('Sum of n Random Matrices (m-by-m)')

For this calculation, spmd is faster than a parfor-loop or parfeval. When you use reduction variables in a parfor-loop, each worker performs a local reduction before sending its partial result back to the client to compute the final result.

By contrast, spmd calls spmdPlus only once to do a global reduction operation, requiring less overhead. As such, the overhead for the reduction part of the calculation is $O (n^{2})$ for spmd, and $O (m n^{2})$ for parfor.