checkGradients
Check first derivative function against finite-difference approximation
Since R2023b
Syntax
Description
valid = checkGradients(fun,x0)fun at a
point near x0 against a finite-difference approximation. By default, the
comparison assumes that the function is an objective function. To check constraint
functions, set the IsConstraint name-value argument to
true.
valid = checkGradients(___,Name=Value)
Examples
The rosen function at the end of this example computes the Rosenbrock objective function and its gradient for a 2-D variable x.
Check that the computed gradient in rosen matches a finite-difference approximation near the point [2,4].
x0 = [2,4]; valid = checkGradients(@rosen,x0)
valid = logical
1
function [f,g] = rosen(x) f = 100*(x(1) - x(2)^2)^2 + (1 - x(2))^2; if nargout > 1 g(1) = 200*(x(1) - x(2)^2); g(2) = -400*x(2)*(x(1) - x(2)^2) - 2*(1 - x(2)); end end
The vecrosen function at the end of this example computes the Rosenbrock objective function in least-squares form and its Jacobian (gradient).
Check that the computed gradient in vecrosen matches a finite-difference approximation near the point [2,4].
x0 = [2,4]; valid = checkGradients(@vecrosen,x0)
valid = logical
1
function [f,g] = vecrosen(x) f = [10*(x(1) - x(2)^2),1-x(1)]; if nargout > 1 g = zeros(2); % Allocate g g(1,1) = 10; % df(1)/dx(1) g(1,2) = -20*x(2); % df(1)/dx(2) g(2,1) = -1; % df(2)/dx(1) g(2,2) = 0; % df(2)/dx(2) end end
The rosen function at the end of this example computes the Rosenbrock objective function and its gradient for a 2-D variable x.
For some initial points, the default forward finite differences cause checkGradients to mistakenly indicate that the rosen function has incorrect gradients. To see result details, set the Display option to "on".
x0 = [0,0];
valid = checkGradients(@rosen,x0,Display="on")____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 1.48826e-06. Supplied derivative element (1,1): -0.126021 Finite-difference derivative element (1,1): -0.126023 checkGradients failed. Supplied derivative and finite-difference approximation are not within 'Tolerance' (1e-06). ____________________________________________________________
valid = logical
0
checkGradients reports a mismatch, with a difference of just over 1 in the sixth decimal place. Use central finite differences and check again.
opts = optimoptions("fmincon",FiniteDifferenceType="central"); valid = checkGradients(@rosen,x0,opts,Display="on")
____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 1.29339e-11. checkGradients successfully passed. ____________________________________________________________
valid = logical
1
Central finite differences are generally more accurate. checkGradients reports that the gradient and central finite-difference approximation match to about 11 decimal places.
function [f,g] = rosen(x) f = 100*(x(1) - x(2)^2)^2 + (1 - x(2))^2; if nargout > 1 g(1) = 200*(x(1) - x(2)^2); g(2) = -400*x(2)*(x(1) - x(2)^2) - 2*(1 - x(2)); end end
The tiltellipse function at the end of this example imposes the constraint that the 2-D variable x is confined to the interior of the tilted ellipse
.
Visualize the ellipse.
f = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2; fcontour(f,LevelList=0) axis([-6 0 -1 7])

Check the gradient of this nonlinear inequality constraint function.
x0 = [-2,6]; valid = checkGradients(@tiltellipse,x0,IsConstraint=true)
valid = 1×2 logical array
1 1
function [c,ceq,gc,gceq] = tiltellipse(x) c = x(1)*x(2)/2 + (x(1) + 2)^2 + (x(2)- 2)^2/2 - 2; ceq = []; if nargout > 2 gc = [x(2)/2 + 2*(x(1) + 2); x(1)/2 + x(2) - 2]; gceq = []; end end
The fungrad function at the end of this example correctly calculates the gradient of some components of the least-squares objective, and incorrectly calculates others.
Examine the second output of checkGradients to see which components do not match well at the point [2,4]. To see result details, set the Display option to "on".
x0 = [2,4];
[valid,err] = checkGradients(@fungrad,x0,Display="on")____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 0.749797. Supplied derivative element (3,2): 19.9838 Finite-difference derivative element (3,2): 5 checkGradients failed. Supplied derivative and finite-difference approximation are not within 'Tolerance' (1e-06). ____________________________________________________________
valid = logical
0
err = struct with fields:
Objective: [3×2 double]
The output shows that element [3,2] is incorrect. But is that the only problem? Examine err.Objective and look for entries that are far from 0.
err.Objective
ans = 3×2
0.0000 0.0000
0.0000 0
0.5000 0.7498
Both the [3,1] and [3,2] elements of the derivative are incorrect. The fungrad2 function at the end of this example corrects the errors.
[valid,err] = checkGradients(@fungrad2,x0,Display="on")____________________________________________________________ Objective function derivatives: Maximum relative difference between supplied and finite-difference derivatives = 2.2338e-08. checkGradients successfully passed. ____________________________________________________________
valid = logical
1
err = struct with fields:
Objective: [3×2 double]
err.Objective
ans = 3×2
10-7 ×
0.2234 0.0509
0.0003 0
0.0981 0.0042
All the differences between the gradient and finite-difference approximations are less than 1e-7 in magnitude.
This code creates the fungrad helper function.
function [f,g] = fungrad(x) f = [10*(x(1) - x(2)^2),1 - x(1),5*(x(2) - x(1)^2)]; if nargout > 1 g = zeros(3,2); g(1,1) = 10; g(1,2) = -20*x(2); g(2,1) = -1; g(3,1) = -20*x(1); g(3,2) = 5*x(2); end end
This code creates the fungrad2 helper function.
function [f,g] = fungrad2(x) f = [10*(x(1) - x(2)^2),1 - x(1),5*(x(2) - x(1)^2)]; if nargout > 1 g = zeros(3,2); g(1,1) = 10; g(1,2) = -20*x(2); g(2,1) = -1; g(3,1) = -10*x(1); g(3,2) = 5; end end
When you provide gradient evaluation functions, nonlinear least-squares solvers such as lsqcurvefit can run faster and more reliably. However, the lsqcurvefit solver has a slightly different syntax for checking gradients compared to other solvers.
Fitting Problem and checkGradient Syntax
To check an lsqcurvefit gradient, instead of passing in the initial point x0 as an array, pass the cell array {x0,xdata}. For example, for the response function , create data ydata from the model with added noise. The response function is fitfun.
function [F,J] = fitfun(x,xdata) F = x(1) + x(2)*exp(-x(3)*xdata); if nargout > 1 J = [ones(size(xdata)) exp(-x(3)*xdata) -xdata.*x(2).*exp(-x(3)*xdata)]; end end
Create xdata as random points from 0 to 10, and ydata as the response plus added noise.
a = 2;
b = 5;
c = 1/15;
N = 100;
rng default
xdata = 10*rand(N,1);
fun = @fitfun;
ydata = fun([a,b,c],xdata) + randn(N,1)/10;Check that the gradient of the response function is correct at the point [a,b,c].
[valid,err] = checkGradients(@fitfun,{[a b c] xdata})valid = logical
1
err = struct with fields:
Objective: [100×3 double]
You can safely use the provided objective gradient. Set the lower bound of all parameters to 0, with no upper bound.
options = optimoptions("lsqcurvefit",SpecifyObjectiveGradient=true);
lb = zeros(1,3);
ub = [];
[sol,res,~,eflag,output] = lsqcurvefit(fun,[1 2 1],xdata,ydata,lb,ub,options)Local minimum possible. lsqcurvefit stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance. <stopping criteria details>
sol = 1×3
2.5872 4.4376 0.0802
res = 1.0096
eflag = 3
output = struct with fields:
firstorderopt: 4.4156e-06
iterations: 25
funcCount: 26
cgiterations: 0
algorithm: 'trust-region-reflective'
stepsize: 1.8029e-04
message: 'Local minimum possible.↵↵lsqcurvefit stopped because the final change in the sum of squares relative to ↵its initial value is less than the value of the function tolerance.↵↵<stopping criteria details>↵↵Optimization stopped because the relative sum of squares (r) is changing↵by less than options.FunctionTolerance = 1.000000e-06.'
bestfeasible: []
constrviolation: []
Nonlinear Constraint Function in lsqcurvefit
The required syntax for nonlinear constraint functions differs from the syntax of the lsqcurvefit objective function. A nonlinear constraint function with gradient has this form:
function [c,ceq,gc,gceq] = ccon(x) c = ... ceq = ... if nargout > 2 gc = ... gceq = ... end end
The gradient expressions must be of size N-by-Nc, where N is the number of problem variables, and Nc is the number of constraint functions. For example, the ccon function below has just one nonlinear inequality constraint. So, the function returns a gradient of size 3-by-1 for this problem with three variables.
function [c,ceq,gc,gceq] = ccon(x) ceq = []; c = x(1)^2 + x(2)^2 + 1/x(3)^2 - 50; if nargout > 2 gceq = []; gc = zeros(3,1); % Gradient is a column vector gc(1) = 2*x(1); gc(2) = 2*x(2); gc(3) = -2/x(3)^3; end end
Check whether the ccon function returns a correct gradient at the point [a,b,c].
[valid,err] = checkGradients(@ccon,[a b c],IsConstraint=true)
valid = 1×2 logical array
1 1
err = struct with fields:
Inequality: [3×1 double]
Equality: []
To use the constraint gradient, set options to use the gradient function, and then solve the problem again with the nonlinear constraint.
options.SpecifyConstraintGradient = true; [sol2,res2,~,eflag2,output2] = lsqcurvefit(@fitfun,[1 2 1],xdata,ydata,lb,ub,[],[],[],[],@ccon,options)
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
sol2 = 1×3
4.4436 2.8548 0.2127
res2 = 2.2623
eflag2 = 1
output2 = struct with fields:
iterations: 15
funcCount: 22
constrviolation: 0
stepsize: 1.7914e-06
algorithm: 'interior-point'
firstorderopt: 3.3350e-06
cgiterations: 0
message: 'Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 1.621619e-07,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.'
bestfeasible: [1×1 struct]
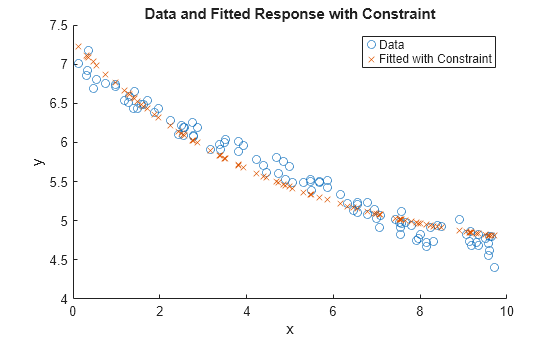
The residual res2 is more than twice as large as the residual res, which has no nonlinear constraint. This result suggests that the nonlinear constraint keeps the solution away from the unconstrained minimum.
Plot the solution with and without the nonlinear constraint.
scatter(xdata,ydata) hold on scatter(xdata,fitfun(sol,xdata),"x") hold off xlabel("x") ylabel("y") legend("Data","Fitted") title("Data and Fitted Response, No Constraint")
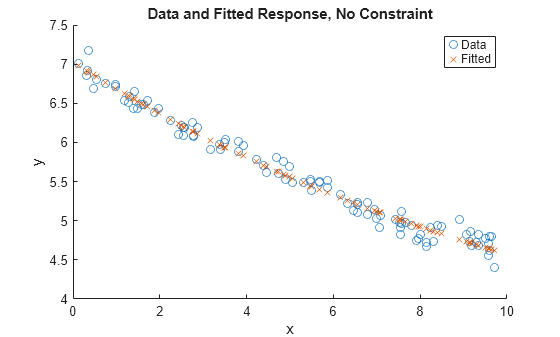
figure scatter(xdata,ydata) hold on scatter(xdata,fitfun(sol2,xdata),"x") hold off xlabel("x") ylabel("y") legend("Data","Fitted with Constraint") title("Data and Fitted Response with Constraint")
Input Arguments
Function to check, specified as a function handle.
If
funrepresents an objective function, thenfunmust have the following signature.[fval,grad] = fun(x)
checkGradientscompares the value ofgrad(x)to a finite-difference approximation for a pointxnearx0. The comparison iswhere
gradrepresents the value of the gradient function, andgrad_fdrepresents the value of the finite-difference approximation.checkGradientsperforms this division component-wise.If
funrepresents a least-squares objective, thenfunis a vector, andgrad(x)is a matrix representing the Jacobian offun.If
funreturns an array ofmcomponents andxhasnelements, wherenis the number of elements ofx0, the JacobianJis anm-by-nmatrix whereJ(i,j)is the partial derivative ofF(i)with respect tox(j). (The JacobianJis the transpose of the gradient ofF.)If
funrepresents a nonlinear constraint, thenfunmust have the following signature.[c,ceq,gc,gceq] = fun(x)
crepresents the nonlinear inequality constraints. Solvers attempt to achievec <= 0. Thecoutput can be a vector of any length.ceqrepresents the nonlinear equality constraints. Solvers attempt to achieveceq = 0. Theceqoutput can be a vector of any length.gcrepresents the gradient of the nonlinear inequality constraints. Your gradient should be of sizeN-by-Nc, whereNis the number of problem variables, andNcis the number of elements ofc.gceqrepresents the gradient of the nonlinear equality constraints. Your gradient should be of sizeN-by-Nceq, whereNis the number of problem variables, andNceqis the number of elements ofceq.
Data Types: function_handle
Location at which to check the gradient, specified as a double array for all solvers
except lsqcurvefit. For lsqcurvefit,
x0 is a 1-by-2 cell array
{x0array,xdata}.
checkGradients checks the gradient at a point near the specified
x0. The function adds a small random direction to
x0, no more than 1e-3 in absolute value. This
perturbation attempts to protect the check against a point where an incorrect gradient
function might pass because of cancellations.
Example: randn(5,1)
Data Types: double
Complex Number Support: Yes
Finite differencing options, specified as the output of
optimoptions. The following options affect finite
differencing.
| Option | Description |
|---|---|
FiniteDifferenceStepSize |
Scalar or vector step size factor for finite differences. When
you set
sign′(x) = sign(x) except sign′(0) = 1.
Central finite differences are
FiniteDifferenceStepSize expands to a vector. The default
is sqrt(eps) for forward finite differences, and eps^(1/3)
for central finite differences.
|
FiniteDifferenceType | Finite differences used to estimate gradients
are either |
TypicalX | Typical |
| DiffMaxChange (discouraged) | Maximum change in variables for
finite-difference gradients (a positive scalar). The default is
|
| DiffMinChange (discouraged) | Minimum change in variables for
finite-difference gradients (a nonnegative scalar). The default is
|
Example: optimoptions("fmincon",FiniteDifferenceStepSize=1e-4)
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: IsConstraint=true,Tolerance=5e-4
Flag to display results at command line, specified as "off" (do
not display the results) or "on" (display the results).
Example: "off"
Data Types: char | string
Flag to check nonlinear constraint gradients, specified as
false (the function is an objective function) or
true (the function is a nonlinear constraint function).
Example: true
Data Types: logical
Tolerance for the gradient approximation, specified as a nonnegative scalar. The
returned value valid is true for each
component where the absolute relative difference between the gradient of
fun and its finite-difference approximation is less than or
equal to Tolerance.
Example: 1e-3
Data Types: double
Output Arguments
Indication that the finite-difference approximation matches the gradient, returned
as a logical scalar for objective functions or a two-element logical vector for
nonlinear constraint functions [c,ceq]. The returned value
valid is true when the absolute relative
difference between the gradient of fun and its finite-difference
approximation is less than or equal to Tolerance for all components
of the gradient. Otherwise, valid is false.
When a nonlinear constraint c or ceq is empty,
the returned value of valid for that constraint is
true.
Relative differences between the gradients and finite-difference approximations,
returned as a structure. For objective functions, the field name is
Objective. For nonlinear constraint functions, the field names are
Inequality (corresponding to c) and
Equality (corresponding to ceq). Each component
of err has the same shape as the supplied derivatives from
fun.
More About
Gradients or Jacobians estimated near the initial point did not match the supplied
derivatives to within a default tolerance of 1e-6 or, for the
checkGradients function, the specified Tolerance
value.
Usually, this failure means that your objective or nonlinear constraint functions have an incorrect derivative calculation. Double-check the indicated derivative.
Occasionally, the finite difference approximations to the derivatives are inaccurate enough to cause the failure. This inaccuracy can occur when the second derivative of a function (objective or nonlinear constraint) has a large magnitude. It can also occur when using the default
'forward'finite differences, which are less accurate but faster than'central'finite differences. If you think that the derivative functions are correct, try one or both of the following to see ifCheckGradientspasses:Set the
FiniteDifferenceTypeoption to'central'.Set the
FiniteDifferenceStepSizeoption to a small value such as1e-10.
Derivatives are checked at a random point near the initial point. Therefore, the gradient check can pass or fail randomly when differing nearby points have differing check results.
For details, see Checking Validity of Gradients or Jacobians.
Version History
Introduced in R2023b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)