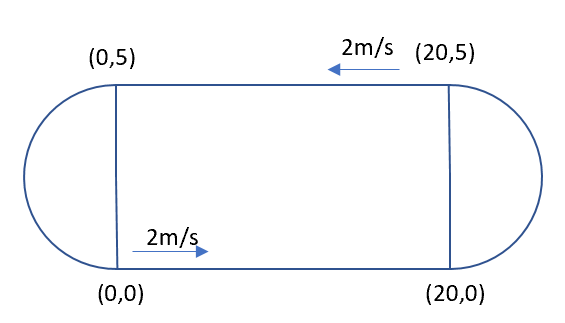waypointTrajectory
Waypoint trajectory generator
Description
The waypointTrajectory
System object™ generates trajectories based on specified waypoints. When you create the
System object, you can choose to specify the time of arrival, velocity, or ground speed at
each waypoint. You can optionally specify other properties such as orientation at each
waypoint. See Algorithms for more details.
To generate a trajectory from waypoints:
Create the
waypointTrajectoryobject and set its properties.Call the object as if it were a function.
To learn more about how System objects work, see What Are System Objects?.
Creation
Syntax
Description
trajectory = waypointTrajectorytrajectory, that generates a trajectory based on default
stationary waypoints.
trajectory = waypointTrajectory(Waypoints,TimeOfArrival)TimeOfArrival property for more details.
Tip
When you specify the TimeOfArrival argument, you must not
specify these properties:
JerkLimitInitialTimeWaitTime
trajectory = waypointTrajectory(Waypoints,GroundSpeed=groundSpeed)GroundSpeed property for more details.
trajectory = waypointTrajectory(Waypoints,Velocities=velocities)Velocities property for more details.
trajectory = waypointTrajectory(___,Name=Value)
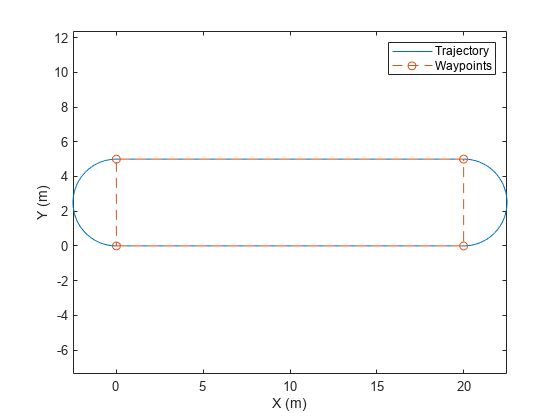
Example: trajectory =
waypointTrajectory([10,10,0;20,20,0;20,20,10],[0,0.5,10]) creates a waypoint
trajectory System object, trajectory, that starts at waypoint
[10,10,0], and then passes through [20,20,0] after
0.5 seconds and [20,20,10] after 10 seconds.
Properties
Usage
Description
[
outputs a frame of trajectory data based on specified creation arguments and
properties.position,orientation,velocity,acceleration,angularVelocity] = trajectory()
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
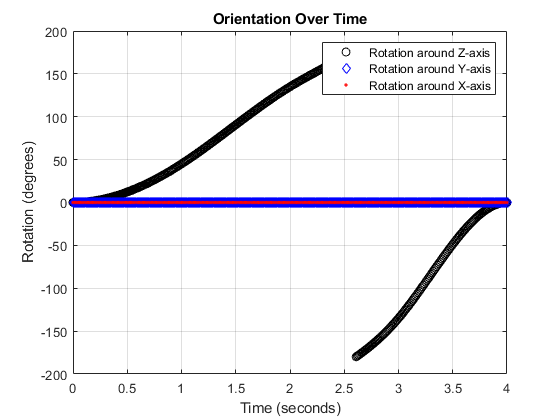
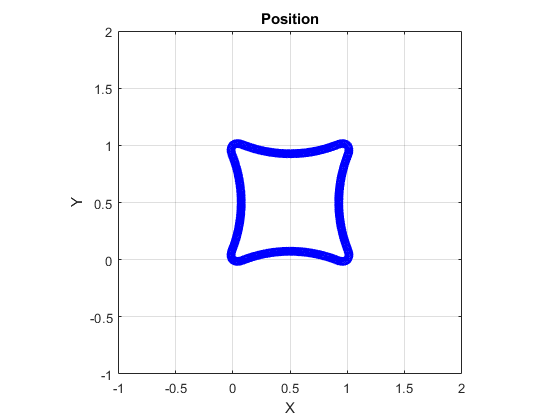
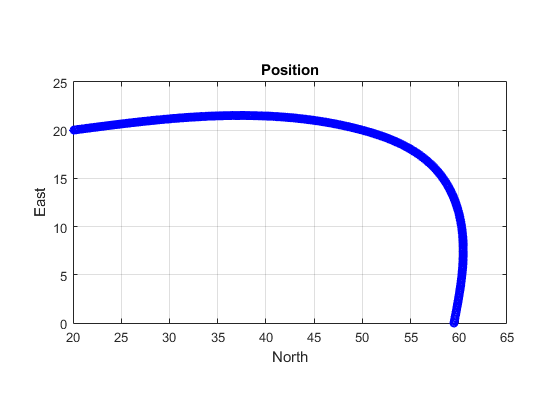
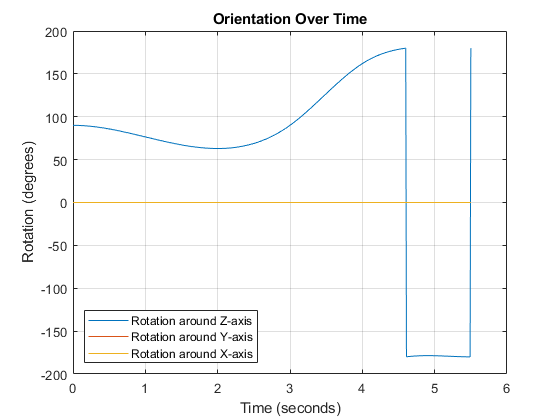
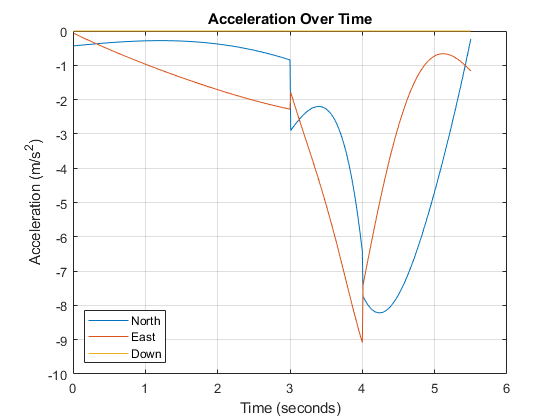
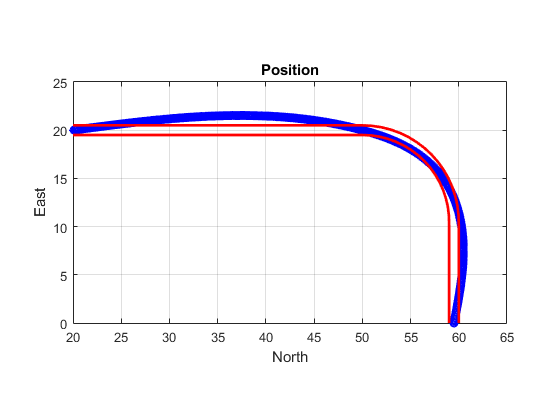
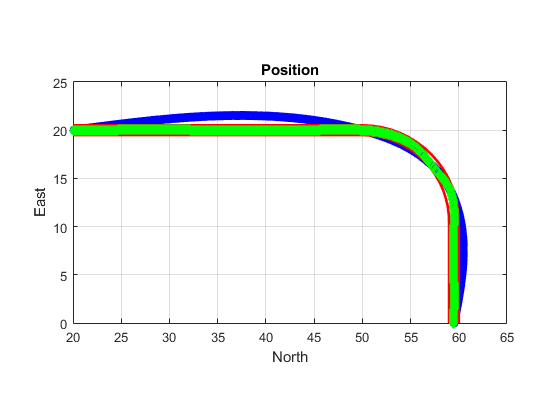
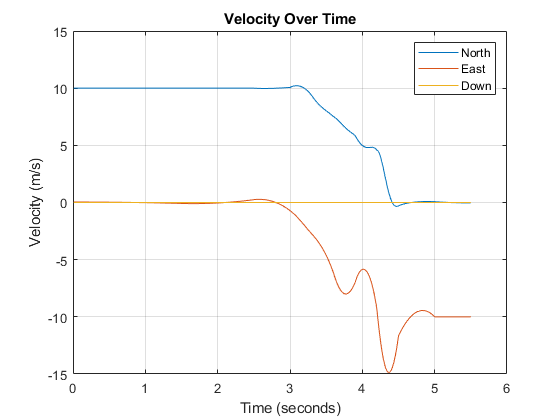
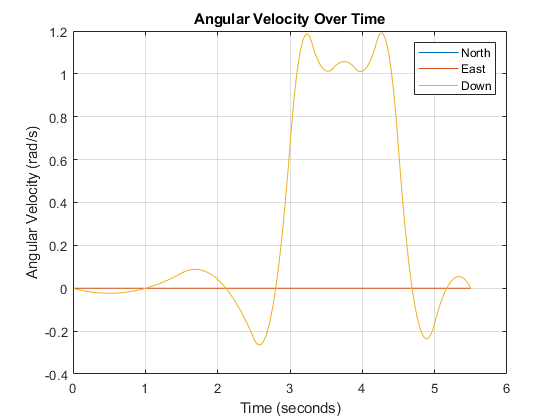
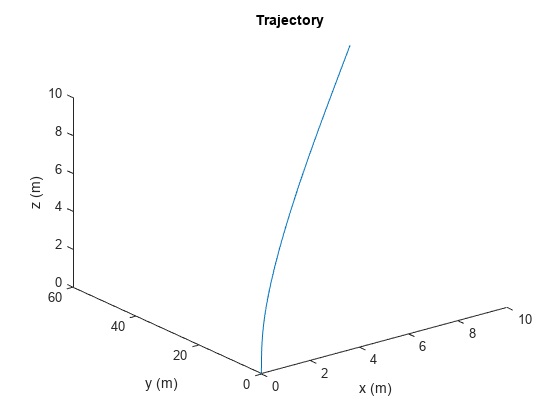
Algorithms
The waypointTrajectory System object defines a trajectory that smoothly passes
through waypoints. The trajectory connects the waypoints through an interpolation that assumes
the gravity direction expressed in the trajectory reference frame is constant. Generally, you
can use waypointTrajectory to model platform or vehicle trajectories within a
hundreds of kilometers distance span.
The planar path of the trajectory (the x-y plane
projection) consists of piecewise, clothoid curves. The curvature of the curve between two
consecutive waypoints varies linearly with the curve length between them. The tangent
direction of the path at each waypoint is chosen to minimize discontinuities in the curvature,
unless the course is specified explicitly via the Course property or
implicitly via the Velocities property. Once the path is established, the
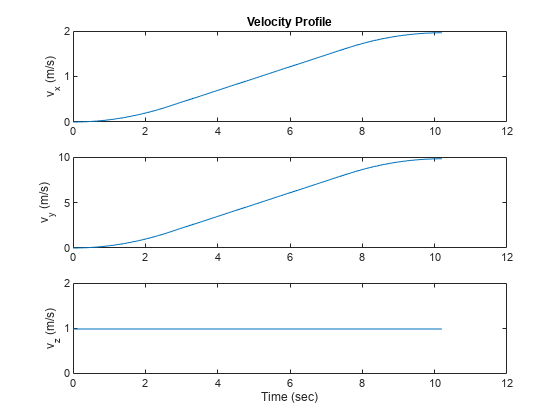
object uses cubic Hermite interpolation to compute the location of the vehicle throughout the
path as a function of time and the planar distance traveled. If the
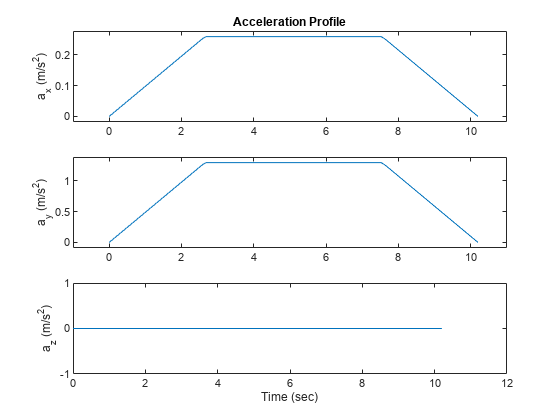
JerkLimit property is specified, the objects produces a horizontal
trapezoidal acceleration profile for any segment that is between two waypoints. The
trapezoidal acceleration profile consists of three subsegments:
A constant-magnitude jerk subsegment
A constant-magnitude acceleration subsegment
A constant-magnitude jerk subsegment
The normal component (z-component) of the trajectory is subsequently
chosen to satisfy a shape-preserving piecewise spline (PCHIP) unless the climb rate is
specified explicitly via the ClimbRate property or the third column of
the Velocities property. Choose the sign of the climb rate based on the
selected ReferenceFrame:
When an 'ENU' reference frame is selected, specifying a positive climb rate results in an increasing value of z.
When an 'NED' reference frame is selected, specifying a positive climb rate results in a decreasing value of z.
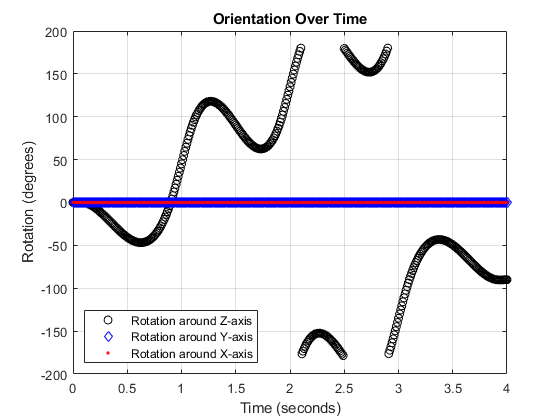
You can define the orientation of the vehicle through the path in two primary ways:
If the
Orientationproperty is specified, then the object uses a piecewise-cubic, quaternion spline to compute the orientation along the path as a function of time.If the
Orientationproperty is not specified, then the yaw of the vehicle is always aligned with the path. The roll and pitch are then governed by theAutoBankandAutoPitchproperty values, respectively.AutoBankAutoPitchDescription falsefalseThe vehicle is always level (zero pitch and roll). This is typically used for large marine vessels. falsetrueThe vehicle pitch is aligned with the path, and its roll is always zero. This is typically used for ground vehicles. truefalseThe vehicle pitch and roll are chosen so that its local z-axis is aligned with the net acceleration (including gravity). This is typically used for rotary-wing craft. truetrueThe vehicle roll is chosen so that its local transverse plane aligns with the net acceleration (including gravity). The vehicle pitch is aligned with the path. This is typically used for two-wheeled vehicles and fixed-wing aircraft.