sort
Sort array elements
Description
B = sort(A)A. By default, sort uses ascending sorted
order.
If
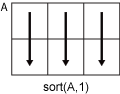
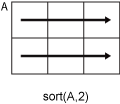
Ais a vector, thensort(A)sorts the vector elements.If
Ais a matrix, thensort(A)treats the columns ofAas vectors and sorts each column.If
Ais a multidimensional array, thensort(A)operates along the first array dimension whose size does not equal 1, treating the elements as vectors.
B = sort(___,Name,Value)sort(A,'ComparisonMethod','abs') sorts
the elements of A by magnitude.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
The
sortrowsfunction provides additional flexibility for subsorting over multiple columns of matrix or table inputs.The
sortfunction and the relational operators use different orderings for complex numbers. For more information, see Relational Operations.
Extended Capabilities
Version History
Introduced before R2006a