Solve ODE

Solve system of ordinary differential equations in the Live Editor

Since R2024b

Description

The Solve ODE task lets you interactively solve a system of ordinary differential equations. The task automatically generates MATLAB^® code for your script.

Using this task, you can:

• Select the form of the system of ordinary differential equations, and specify the system by writing a function using a provided template.

• Specify the Jacobian, events, and initial slope.

• Use an automatically selected solver or select a solver, and specify solver options such as tolerances.

• Solve the ODE for a specified time interval and number of interpolation points per step.

• Visualize the solutions of the ODE while the solver runs or when the solver finishes.

For more information about Live Editor tasks generally, see Add Interactive Tasks to a Live Script.

×

Open the Task

To add the Solve ODE task to a live script in the MATLAB Editor:

• On the Live Editor tab, select Task > Solve ODE.

• In a code block in the script, type a relevant keyword, such as ode. Select Solve ODE from the suggested command completions.

Examples

Solve Single ODE

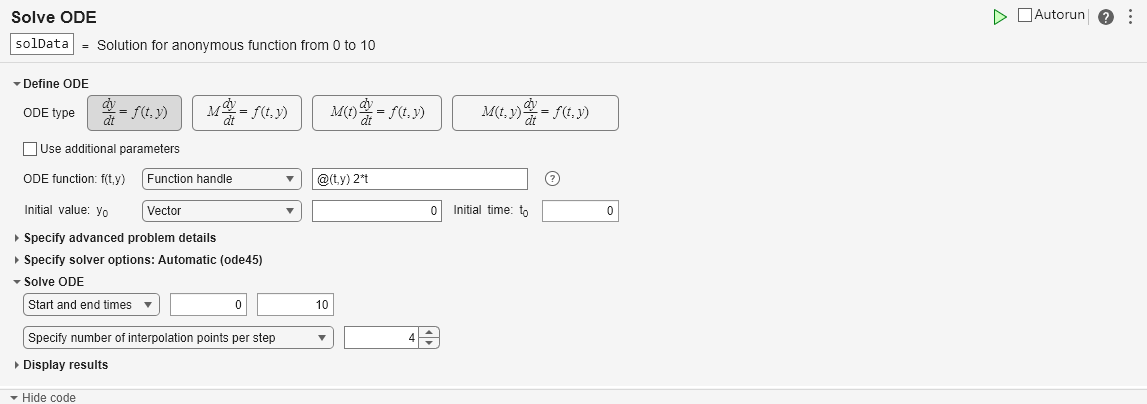
Interactively solve the ODE $\frac{\mathit{dy}}{\mathit{dt}}=2\mathit{t}$ over the time interval [0 10] with an initial value of $\mathit{y}\left(0\right)=0$.

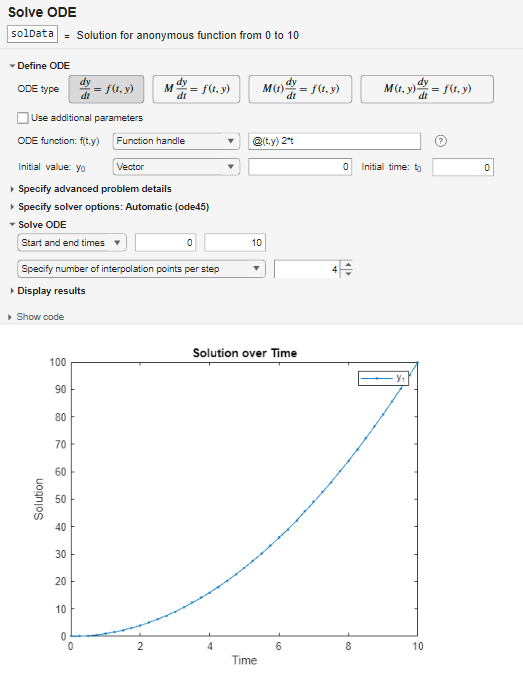
Open the Solve ODE task in the Live Editor. To define the ODE, select the $\frac{\mathit{dy}}{\mathit{dt}}=\mathit{f}\left(\mathit{t},\mathit{y}\right)$ ODE type. Specify the ODE as a function handle, entering @(t,y) 2*t in the corresponding box. Then specify the initial value as a single-element vector, entering 0 in the corresponding box. Specify the initial time as 0 and start and end times as 0 and 10.

To solve the ODE, run the task by clicking the Run current section button in the top-right corner of the task window. By default, the task plots the solution to the ODE over time after the equation is solved. To see the code that this task generates, expand the task display by clicking Show code at the bottom of the task parameter area.

% Define ODE problem and specify solver options
odeObj = ode(ODEFcn = @(t,y) 2*t, ...
    InitialValue = 0);

% Solve ODE problem
solData = solve(odeObj,0,10);

% Plot solution over time
plot(solData.Time,solData.Solution,".-");
ylabel("Solution")
xlabel("Time")
title("Solution over Time")
legend("y_1")

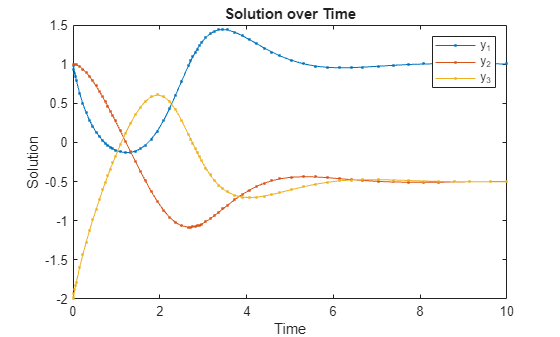
clear odeObj

Solve System of DAEs with Mass Matrix

Solve this system of first-order differential algebraic equations (DAEs) by using a mass matrix with the Solve ODE Live Editor task.

$$\begin{array}{l}{{\mathit{y}}_1}^{\prime }={\mathit{y}}_1{\mathit{y}}_3-{\mathit{y}}_2\\ {{\mathit{y}}_2}^{\prime }={\mathit{y}}_1-1\\ 0={\mathit{y}}_1+{\mathit{y}}_2+{\mathit{y}}_3\end{array}$$

Rewriting the system in the form $\mathit{M}\frac{\mathit{dy}}{\mathit{dt}}=\mathit{f}\left(\mathit{t},\mathit{y}\right)$ shows a constant, singular mass matrix on the left side.

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{{\mathit{y}}_1}^{\prime }\\ {{\mathit{y}}_2}^{\prime }\\ {{\mathit{y}}_3}^{\prime }\end{array}\right]=\left[\begin{array}{c}{\mathit{y}}_1{\mathit{y}}_3-{\mathit{y}}_2\\ {\mathit{y}}_1-1\\ {\mathit{y}}_1+{\mathit{y}}_2+{\mathit{y}}_3\end{array}\right]$$

In a live script, create a local function and mass matrix to represent the problem.

function out = odefun(t,y)
out = [y(1)*y(3)-y(2); 
    y(1)-1; 
    y(1)+y(2)+y(3)];
end
massmatrix = [1 0 0; 0 1 0; 0 0 0];

In the same live script, open the Solve ODE task, and select the $\mathit{M}\frac{\mathit{dy}}{\mathit{dt}}=\mathit{f}\left(\mathit{t},\mathit{y}\right)$ ODE type. Select the odefun and massmatrix local variables for the ODE function and mass matrix, respectively. Set the initial time as 0 and the initial value vector as [1 1 -2] to indicate that ${\mathit{y}}_1\left(0\right)=1$, ${\mathit{y}}_2\left(0\right)=1$, and ${\mathit{y}}_3\left(0\right)=-2$. Solve the equations over the time interval [0 10].

To solve the system, run the task by clicking the Run current section button in the top-right corner of the task window.

% Define ODE problem and specify solver options
odeObj = ode(ODEFcn = @odefun, ...
    InitialValue = [1 1 -2], ...
    MassMatrix = massmatrix);

% Solve ODE problem
solData = solve(odeObj,0,10);

% Plot solution over time
plot(solData.Time,solData.Solution([1 2 3],:),".-");
ylabel("Solution")
xlabel("Time")
title("Solution over Time")
legend("y_1","y_2","y_3")

clear odeObj

Related Examples

• Add Interactive Tasks to a Live Script

Parameters

ODE function — System of ordinary differential equations to solve

local function | function handle | function file

To specify the equations to solve, first select one of these options and then specify the corresponding function:

• Local function — Select the local function from the provided list. To create a new local function, click New. A new function definition appears at the bottom of the script. Edit the function so that it returns the right side of the ODE.

• Function handle — Create the function handle in the text box.

• From file — Click the browse button and select the function file. To create a new function file, click New. A new function file appears. Edit the file so that the function returns the right side of the ODE, and save the file on the MATLAB path. Then click the browse button and select the file.

Additional parameters — Equation parameters

array

Select Use additional parameters and then select an array of any size or data type in the workspace to specify the equation parameters. These array values can be supplied to any of the functions used for the ODE function, Jacobian, or event definition by specifying an extra input argument in the function.

For example, for an ODE function handle @(t,y,p) 5*y*p(1)-3*p(2) that uses the parameters p(1) and p(2), specify one parameter array p = [2 3] so that the task uses the parameter values p(1) = 2 and p(2) = 3 when solving the ODE.

Mass matrix — Mass matrix

matrix | local function | function handle | function file

If the mass matrix is constant, select a variable from the provided list. If the mass matrix is not constant, first select one of these options and then specify the corresponding function:

• Local function — Select the local function from the provided list. To create a new local function, click New. A new function definition appears at the bottom of the script. Edit the function to define the mass matrix.

• Function handle —Create the function handle in the text box.

• From file — Click the browse button and select the function file. To create a new function file, click New. A new function file appears. Edit the file so that the function defines the mass matrix, and save the file on the MATLAB path. Then click the browse button and select the file.

You can also specify whether the mass matrix is singular and whether the state dependence is weak or strong.

Jacobian — Jacobian matrix

local function | function handle | function file | matrix

To set the Jacobian, in the Specify advanced problem details section, click the Jacobian button. In the first list, select whether you want to specify the Jacobian as a function, a constant matrix, or a sparsity pattern.

To specify the Jacobian as a function, first select one of these options and then specify the corresponding function:

• Local function — Select the local function from the provided list. To create a new local function, click New. A new function definition appears at the bottom of the script. Edit the function to define the Jacobian.

• Function handle — Create the function handle in the text box.

• From file — Click the browse button and select the function file. To create a new function file, click New. A new function file appears. Edit the file so that the function defines the Jacobian, and save the file on the MATLAB path. Then click the browse button and select the file.

To specify the Jacobian as a constant matrix, select a variable from the provided list.

To specify the Jacobian as a sparsity pattern, select a variable from the provided list.

Event definition — Events to detect

local function | function handle | function file

To set event definitions, in the Specify advanced problem details section, click the Events button. To specify the events to detect, first select one of these options and then specify the corresponding function:

• Local function — Select the local function from the provided list. To create a new local function, click New. A new function definition appears at the bottom of the script. Edit the function to define the event.

• Function handle — Create the function handle in the text box.

• From file — Click the browse button and select the function file. To create a new function file, click New. A new function file appears. Edit the file so that the function defines the event, and save the file on the MATLAB path. Then click the browse button and select the file.

You can also specify the direction of zero crossings to detect (as ascending, descending, or both) and how to respond to detected events (by proceeding, stopping, or executing a specified callback function).

Version History

Introduced in R2024b