prod
Product of array elements
Syntax
Description
B = prod(A)A.
If
Ais a vector, thenprod(A)returns the product of the elements.If
Ais a nonempty matrix, thenprod(A)treats the columns ofAas vectors and returns a row vector of the products of each column.If
Ais an empty 0-by-0 matrix,prod(A)returns1.If
Ais a multidimensional array, thenprod(A)acts along the first nonsingleton dimension and returns an array of products. The size ofBin this dimension reduces to1, while the sizes of all other dimensions remain the same as inA.If
Ais a table or timetable, thenprod(A)returns a one-row table of the products of each variable. (since R2023a)
prod computes and returns B as
single when the input, A, is
single. For all other numeric and logical data types,
prod computes and returns B as
double.

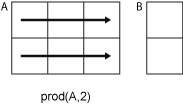
![prod(A,[1 2]) collapses the pages of a 2-by-3-by-3 array into a 1-by-1-by-3 array.](sum_vecdim.png)