polarbubblechart
Polar bubble chart
Syntax
Description
Vector and Matrix Data
polarbubblechart(
displays colored circular markers (bubbles) at the locations specified by the vectors
theta,rho,sz)theta and rho. The bubble sizes are specified by
sz.
To plot one set of coordinates, specify
theta,rho, andszas vectors of equal length.To plot multiple sets of coordinates on the same set of axes, specify at least one of
theta,rho, orszas a matrix.
Table Data
polarbubblechart(
plots the variables tbl,thetavar,rhovar,sizevar)thetavar and rhovar from the
table tbl and uses the variable sizevar for the
bubble sizes. To plot one data set, specify one variable each for
thetavar, rhovar, and sizevar.
To plot multiple data sets, specify multiple variables for at least one of those
arguments. The arguments that specify multiple variables must specify the same number of
variables.
Additional Options
polarbubblechart(
displays the bubble chart in the target axes pax,___)pax. Specify the axes
before all other input arguments.
polarbubblechart(___,
specifies Name,Value)BubbleChart properties using one or more name-value
arguments. Specify the properties after all other input arguments. For a list of
properties, see BubbleChart Properties.
bc = polarbubblechart(___) returns the
BubbleChart object. Use bc to modify properties of
the chart after creating it. For a list of properties, see BubbleChart Properties.
Examples
Define a set of bubble coordinates as the vectors th and r. Define sz as a vector of bubble sizes. Then create a bubble chart of these values.
th = linspace(0,2*pi,10); r = rand(1,10); sz = rand(1,10); polarbubblechart(th,r,sz);

Define a set of bubble coordinates as the vectors th and r. Define sz as a vector of bubble sizes. Then create a bubble chart and specify the color as red. By default, the bubbles are partially transparent.
th = 1:10;
r = rand(1,10);
sz = rand(1,10);
polarbubblechart(th,r,sz,'red');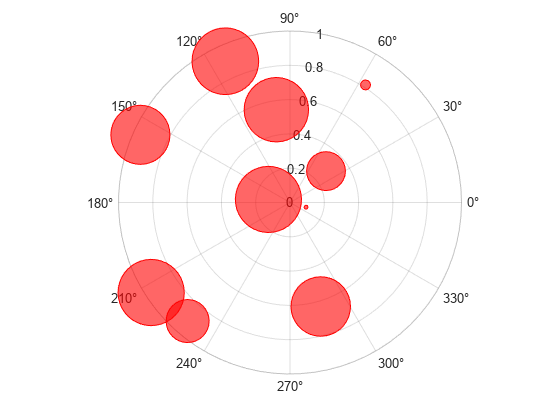
For a custom color, you can specify an RGB triplet or a hexadecimal color code. For example, the hexadecimal color code '#7031BB', specifies a shade of purple.
polarbubblechart(th,r,sz,'#7031BB');
You can also specify a different color for each bubble. For example, specify a vector to select colors from the figure's colormap.
c = 1:10; polarbubblechart(th,r,sz,c)

Define a set of bubble coordinates as the vectors th and r. Define sz as a vector of bubble sizes. Then create a bubble chart. By default, the bubbles are 60% opaque, and the edges are completely opaque with the same color.
th = linspace(0,2*pi,10); r = rand(1,10); sz = rand(1,10); polarbubblechart(th,r,sz);

You can customize the opacity and the outline color by setting the MarkerFaceAlpha and MarkerEdgeColor properties, respectively. One way to set a property is by specifying a name-value pair argument when you create the chart. For example, you can specify 20% opacity by setting the MarkerFaceAlpha value to 0.20.
bc = polarbubblechart(th,r,sz,'MarkerFaceAlpha',0.20);
If you create the chart by calling the polarbubblechart function with a return argument, you can use the return argument to set properties on the chart after creating it. For example, you can change the outline color to purple.
bc.MarkerEdgeColor = [0.5 0 0.5];

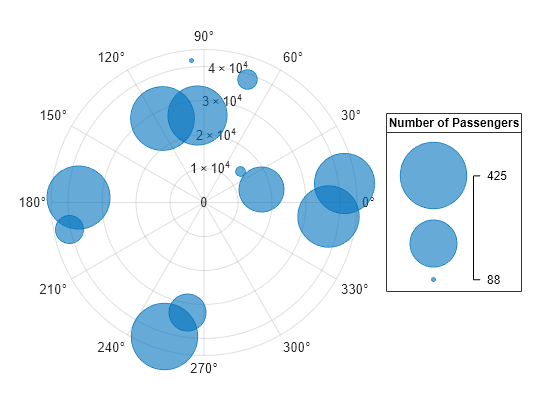
Define a data set that shows the incoming air traffic at a certain airport over a certain period of time.
Define
thetaas a vector of angles of approach for the incoming planes.Define
altitudeas a vector of altitudes.Define
planesizeas a vector of plane sizes, measured in the number of passengers.
Then display the data in a bubble chart with a bubble legend that shows the relationship between the bubble sizes and the number of passengers on the planes.
theta = repmat([0 pi/2 7*pi/6],1,4) + 0.25*randn(1,12); altitude = randi([13000 43000],1,12); planesize = randi([75 500],[1 12]); polarbubblechart(theta,altitude,planesize) bubblelegend('Number of Passengers','Location','eastoutside')
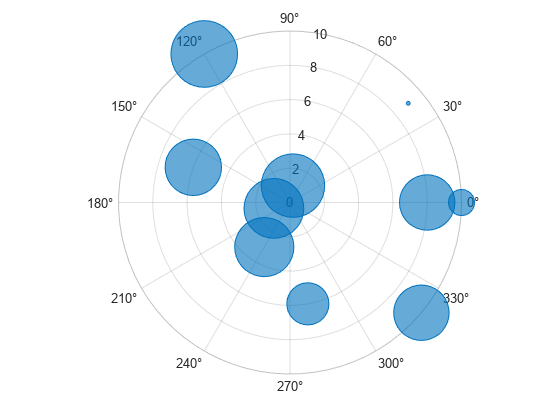
A convenient way to plot data from a table is to pass the table to the polarbubblechart function and specify the variables you want to plot. For example, create a table with four variables. Plot the 'Th' and 'R1' variables, and vary the bubble sizes according to the 'Sz' variable.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R1 = randi([0 10],10,1); R2 = randi([20 30],10,1); Sz = rand(10,1); tbl = table(Th,R1,R2,Sz); % Create polar bubble chart polarbubblechart(tbl,'Th','R1','Sz')
You can also plot multiple variables at the same time. For example, plot two sets of radius values by specifying the rhovar argument as the cell array {'R1','R2'}. Then add a legend. The legend labels match the variable names.
polarbubblechart(tbl,'Th',{'R1','R2'},'Sz') legend

You can plot data from a table and customize the colors by specifying the cvar argument when you call the polarbubblechart function.
For example, create a table with four variables of random numbers, and plot the Th and R variables. Vary the bubble sizes according to the Sz variable, and vary the colors according to the Colors variable.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R = randi([0 10],10,1); Sz = rand(10,1); Colors = rand(10,1); tbl = table(Th,R,Sz,Colors); % Create polar bubble chart polarbubblechart(tbl,'Th','R','Sz','Colors')

Define two data sets showing the incoming air traffic at two different airports over a certain period of time.
Define
theta1andtheta2as vectors containing the angles of approach for the incoming planes.Define
planesize1andplanesize2as a vectors of plane sizes, measured in the number of passengers.Define
altitude1andaltitude2as vectors containing the altitudes for the planes.
theta1 = repmat([0 pi/2 7*pi/6],1,4) + 0.25*randn(1,12); theta2 = repmat([pi pi/6 3*pi/2],1,4) + 0.25*randn(1,12); planesize1 = randi([75 500],[1 12]); planesize2 = randi([1 50],[1 12]); altitude1 = randi([13000 43000],1,12); altitude2 = randi([13000 85000],1,12);
Create a tiled chart layout so you can visualize the data side-by-side. Then, create a polar axes object in the first tile, plot the data for the first airport, and add a title. Then repeat the process in the second tile for the second airport.
t = tiledlayout(1,2); pax1 = polaraxes(t); polarbubblechart(pax1,theta1,altitude1,planesize1) title('Airport A') pax2 = polaraxes(t); pax2.Layout.Tile = 2; polarbubblechart(pax2,theta2,altitude2,planesize2); title('Airport B')

Reduce all the bubble sizes to make it easier to see all the bubbles. In this case, change the range of diameters to be between 5 and 20 points.
bubblesize(pax1,[5 20]) bubblesize(pax2,[5 20])
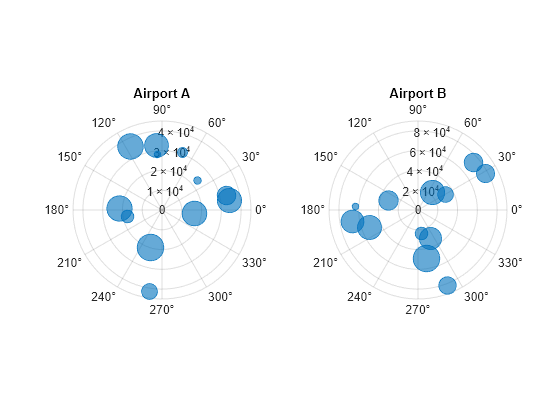
The planes at Airport A are generally much smaller than at Airport B, but the bubble sizes do not reflect this information in the preceding charts. This is because the smallest and largest bubbles map to the smallest and largest data points in each of the axes. To display the bubbles on the same scale, define a vector called allsizes that includes the plane sizes at both airports. Then use the bubblelim function to reset the scaling for both charts.
allsizes = [planesize1 planesize2]; newlims = [min(allsizes) max(allsizes)]; bubblelim(pax1,newlims) bubblelim(pax2,newlims)

Input Arguments
theta values, specified as a scalar, vector, or matrix. The size
and shape of theta depends on the shape of your data. This table
describes the most common situations.
| Type of Bubble Chart | How to Specify Coordinates |
|---|---|
| Single bubble | Specify polarbubblechart(pi/2,0.5,1) |
| One set of bubbles | Specify theta = [0 pi/4 pi/2]; rho = [1; 2; 3]; sz = [10 11 12]; polarbubblechart(theta,rho,sz) |
| Multiple sets of bubbles that are different colors | If all the data sets share the same theta = [0 pi/4 pi/2]; rho = [4 5 6; 7 8 9]; sz = [1 2 3]; polarbubblechart(theta,rho,sz) polarbubblechart plots a
separate set of bubbles for each column in the
matrix.Alternatively, specify theta = [0 pi/6 pi/2; pi/8 pi/4 pi]; rho = [1 2 3; 4 5 6]; sz = [10 20 30; 40 50 60]; polarbubblechart(theta,rho,sz) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
rho values, specified as a scalar, vector, or matrix. The size
and shape of rho depends on the shape of your data. This table
describes the most common situations.
| Type of Bubble Chart | How to Specify Coordinates |
|---|---|
| Single bubble | Specify polarbubblechart(pi/2,0.5,1) |
| One set of bubbles | Specify theta = [0 pi/4 pi/2]; rho = [1; 2; 3]; sz = [10 11 12]; polarbubblechart(theta,rho,sz) |
| Multiple sets of bubbles that are different colors | If all the data sets share the same theta = [0 pi/4 pi/2]; rho = [4 5 6; 7 8 9]; sz = [1 2 3]; polarbubblechart(theta,rho,sz) polarbubblechart plots a
separate set of bubbles for each column in the
matrix.Alternatively, specify theta = [0 pi/6 pi/2; pi/8 pi/4 pi]; rho = [1 2 3; 4 5 6]; sz = [10 20 30; 40 50 60]; polarbubblechart(theta,rho,sz) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Bubble sizes, specified as a numeric scalar, vector, or matrix. The way you specify
the size depends on how you specify theta and rho
and how you want the chart to look. This table describes the most common
situations.
| Type of Bubble Chart | theta and rho
| sz | Example |
|---|---|---|---|
One set of bubbles | Vectors of the same length | A vector with the same length as | Specify theta = [0 pi/4 pi/3 pi/2]; rho = [1 2 3 4]; sz = [10 20 30 40]; polarbubblechart(theta,rho,sz) |
Multiple sets of bubbles that have varied coordinates and bubble sizes | At least one of | A matrix that has the same size as the | Specify theta = [0 pi/4 pi/3 pi/2]; rho = [1 5; 2 6; 3 7; 4 8]; sz = [10 20; 30 40; 50 60; 70 80]; polarbubblechart(theta,rho,sz) |
Multiple sets of bubbles, where all the coordinates are shared, but the sizes are different for each set | Vectors of the same length | A matrix with at least one dimension that matches the lengths of
| Specify theta = [0 pi/4 pi/3 pi/2]; rho = [1 2 3 4]; sz = [10 20; 30 40; 50 60; 70 80]; polarbubblechart(theta,rho,sz) |
Multiple sets of bubbles, where the coordinates vary in at least one dimension, but the sizes are shared between sets | At least one of | A vector with the same number of elements as there are bubbles in each data set | Specify theta = [0 pi/4 pi/3 pi/2]; rho = [1 5; 2 6; 3 7; 4 8]; sz = [10 20 30 40]; polarbubblechart(theta,rho,sz) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Bubble color, specified as a color name, RGB triplet, matrix of RGB triplets, or a vector of colormap indices.
Color name — A color name such as
"red", or a short name such as"r".RGB triplet — A three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7]. RGB triplets are useful for creating custom colors.Matrix of RGB triplets — A three-column matrix in which each row is an RGB triplet.
Vector of colormap indices — A vector of numeric values that is the same length as the
thetaandrhovectors.
The way you specify the color depends on your preferred color scheme and whether you are plotting one set of bubbles or multiple sets of bubbles. This table describes the most common situations.
| Color Scheme | How to Specify the Color | Example |
|---|---|---|
Use one color for all the bubbles. | Specify a color name or a short name from the table below, or specify one RGB triplet. | Display one set of bubbles, and specify the color as
theta = [0 pi/4 pi/3 pi/2];
rho = [1 2 3 4];
sz = [10 20 30 40];
polarbubblechart(theta,rho,sz,'red')Display
two sets of bubbles, and specify the color as red using the RGB triplet
theta = [0 pi/4 pi/3 pi/2]; rho = [1 5; 2 6; 3 7; 4 8]; sz = [10 20; 30 40; 50 60; 70 80]; polarbubblechart(theta,rho,sz,[1 0 0]) |
Assign different colors to each bubble using a colormap. | Specify a row or column vector of numbers. The numbers map into the current colormap array. The smallest value maps to the first row in the colormap, and the largest value maps to the last row. The intermediate values map linearly to the intermediate rows. If your chart has three bubbles, specify a column vector to ensure the values are interpreted as colormap indices. You can use this method only when
| Create a vector c = [1 2 3 4];
theta = [0 pi/4 pi/3 pi/2];
rho = [1 2 3 4];
sz = [10 20 30 40];
polarbubblechart(theta,rho,sz,c)
colormap(gca,"winter") |
Create a custom color for each bubble. | Specify an m-by-3 matrix of RGB triplets, where m is the number of bubbles. You can use this method only when
| Create a matrix c = [0 1 0; 1 0 0; 0.5 0.5 0.5; 0.6 0 1]; theta = [0 pi/4 pi/3 pi/2]; rho = [1 2 3 4]; sz = [10 20 30 40]; polarbubblechart(theta,rho,sz,c) |
Create a different color for each data set. | Specify an n-by-3 matrix of RGB triplets, where n is the number of data sets. You can use this method only when at least one of
| Create a matrix c = [1 0 0; 0.6 0 1]; theta = [0 pi/4 pi/3 pi/2]; rho = [1 5; 2 6; 3 7; 4 8]; sz = [10 20; 30 40; 50 60; 70 80]; polarbubblechart(theta,rho,sz,c) |
Color Names and RGB Triplets for Common Colors
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Source table containing the data to plot, specified as a table or a timetable.
Table variables containing the theta values, specified as one or more table variable indices.
Specifying Table Indices
Use any of the following indexing schemes to specify the desired variable or variables.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
Plotting Your Data
The table variables you specify can contain any numeric data type.
To plot one data set, specify one variable each for thetavar,
rhovar, sizevar, and optionally
cvar. For example, create a table with four variables. Plot the
Th and R1 variables, and vary the bubble sizes
according to the Sz
variable.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R1 = randi([0 10],10,1); R2 = randi([20 30],10,1); Sz = rand(10,1); tbl = table(Th,R1,R2,Sz); % Create polar bubble chart polarbubblechart(tbl,'Th','R1','Sz')
To plot multiple data sets together, specify multiple variables for at least one of
thetavar, rhovar, sizevar, or
optionally cvar. If you specify multiple variables for more than one
argument, the number of variables must be the same for each of those arguments.
For example, plot the Th variable on the theta-axis and
the R1 and R2 variables on the
r-axis. Specify the Sz variable for the bubble
sizes.
polarbubblechart(tbl,'Th',{'R1','R2'},'Sz')
You can also use different indexing schemes for the table variables. For example, specify thetavar as a variable name, rhovar as an index number, and sizevar as a logical vector.
polarbubblechart(tbl,'Th',2,[false false true])Table variables containing the rho values, specified as one or more table variable indices.
Specifying Table Indices
Use any of the following indexing schemes to specify the desired variable or variables.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
Plotting Your Data
The table variables you specify can contain any numeric data type.
To plot one data set, specify one variable each for thetavar,
rhovar, sizevar, and optionally
cvar. For example, create a table with four variables. Plot the
Th and R1 variables, and vary the bubble sizes
according to the Sz
variable.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R1 = randi([0 10],10,1); R2 = randi([20 30],10,1); Sz = rand(10,1); tbl = table(Th,R1,R2,Sz); % Create polar bubble chart polarbubblechart(tbl,'Th','R1','Sz')
To plot multiple data sets together, specify multiple variables for at least one of
thetavar, rhovar, sizevar, or
optionally cvar. If you specify multiple variables for more than one
argument, the number of variables must be the same for each of those arguments.
For example, plot the Th variable on the theta-axis and
the R1 and R2 variables on the
r-axis. Specify the Sz variable for the bubble
sizes.
polarbubblechart(tbl,'Th',{'R1','R2'},'Sz')
You can also use different indexing schemes for the table variables. For example, specify thetavar as a variable name, rhovar as an index number, and sizevar as a logical vector.
polarbubblechart(tbl,'Th',2,[false false true])Table variables containing the bubble size data, specified as one or more table variable indices.
Specifying Table Indices
Use any of the following indexing schemes to specify the desired variable or variables.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
Plotting Your Data
The table variables you specify can contain any type of numeric values.
If you are plotting one data set, specify one variable for
sizevar. For example, create a table with four variables. Plot
the Th and R variables, and vary the bubble
sizes according to the Sz1
variable.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R = randi([0 10],10,1); Sz1 = rand(10,1); Sz2 = rand(10,1); tbl = table(Th,R,Sz1,Sz2); % Create polar bubble chart polarbubblechart(tbl,'Th','R','Sz1')
If you are plotting multiple data sets, you can specify multiple variables for at
least one of thetavar, rhovar,
sizevar, or optionally cvar. If you specify
multiple variables for more than one argument, the number of variables must be the
same for each of those arguments.
For example, plot the Th variable on the
theta-axis and the R variable on the
r-axis. Specify the Sz1 and
Sz2 variables for the bubble sizes. The resulting plot shows two
sets of bubbles with the same coordinates, but different bubble
sizes.
polarbubblechart(tbl,'Th','R',{'Sz1','Sz2'})
Table variables containing the bubble color data, specified as one or more table variable indices.
Specifying Table Indices
Use any of the following indexing schemes to specify the desired variable or variables.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
Plotting Your Data
The table variables you specify can contain values of any numeric type. Each variable can be:
A column of numbers that linearly map into the current colormap.
A three-column array of RGB triplets. RGB triplets are three-element vectors whose values specify the intensities of the red, green, and blue components of specific colors. The intensities must be in the range
[0,1]. For example,[0.5 0.7 1]specifies a shade of light blue.
If you are plotting one data set, specify one variable for
cvar. For example, create a table with six variables of random
numbers. Plot the Th and R1 variables. Vary the
bubble sizes according to the Sz variable, and vary the colors
according to the Color1
variable.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R1 = randi([0 10],10,1); R2 = randi([20 30],10,1); Sz = rand(10,1); Color1 = rand(10,1); Color2 = rand(10,1); tbl = table(Th,R1,R2,Sz,Color1,Color2); % Create polar bubble chart polarbubblechart(tbl,'Th','R1','Sz','Color1')
If you are plotting multiple data sets, you can specify multiple variables for at
least one of thetavar, rhovar,
sizevar, or cvar. If you specify multiple
variables for more than one argument, the number of variables must be the same for
each of those arguments.
For example, plot the Th variable on the
theta-axis and the R1 and
R2 variables on the r-axis. Vary the bubble
sizes according to the Sz variable. Specify the
Color1 and Color2 variables for the colors.
The resulting plot shows two sets of bubbles with the same
theta-coordinates and bubble sizes, but different
r-coordinates and
colors.
polarbubblechart(tbl,'Th',{'R1','R2'},'Sz',{'Color1','Color2'})
Target axes, specified as a PolarAxes object. If you do not
specify the axes, MATLAB® plots into the current axes, or it creates a PolarAxes
object if one does not exist.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: bubblechart([1 2 3],[4 10 9],[1 2 3],'MarkerFaceColor','red')
creates red bubbles.
Note
The properties listed here are only a subset. For a complete list, see BubbleChart Properties.
Marker outline color, specified "flat", an RGB triplet, a hexadecimal color
code, a color name, or a short name. The default value of "flat" uses
colors from the CData property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Example: [0.5 0.5 0.5]
Example: "blue"
Example: "#D2F9A7"
Marker fill color, specified as 'flat', 'auto', an RGB triplet, a hexadecimal color code, a color name, or a short name. The 'flat' option uses the CData values. The 'auto' option uses the same color as the Color property for the axes.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Example: [0.3 0.2 0.1]
Example: 'green'
Example: '#D2F9A7'
Width of marker edge, specified as a positive value in point units.
Example: 0.75
Marker edge transparency, specified as a scalar in the range [0,1]
or 'flat'. A value of 1 is opaque and 0 is completely transparent.
Values between 0 and 1 are semitransparent.
To set the edge transparency to a different value for each point in the plot, set the
AlphaData property to a vector the same size as the
XData property, and set the
MarkerEdgeAlpha property to 'flat'.
Marker face transparency, specified as a scalar in the range [0,1] or 'flat'. A value of 1 is opaque and 0 is completely transparent. Values between 0 and 1 are partially transparent.
To set the marker face transparency to a different value for each point, set the AlphaData property to a vector the same size as the XData property, and set the MarkerFaceAlpha property to 'flat'.
Version History
Introduced in R2020bWhen you pass a table and one or more variable names to the polarbubblechart function, the legend labels now display any special characters that are included in the table variable names, such as underscores. Previously, special characters were interpreted as TeX or LaTeX characters.
For example, if you pass a table containing a variable named Sample_Number
to the polarbubblechart function and then display a legend, the
underscore appears in the legend label. In R2022a and earlier releases, the
underscore is interpreted as a subscript.
| Release | Label for Table Variable "Sample_Number" |
|---|---|
R2022b |
|
R2022a |
|
To display legend labels with TeX or LaTeX formatting, call the legend
function with the desired label strings after plotting. For example:
legend(["Sample_Number" "Another_Legend_Label"])
The polarbubblechart function now accepts combinations of vectors and matrices for the coordinates and size data. As a result, you can visualize multiple data sets at once rather than using the hold function between plotting commands.
Create plots by passing a table to the polarbubblechart function followed by the variables you want to plot. When you specify your data as a table, the axis labels and the legend (if present) are automatically labeled using the table variable names.
See Also
Functions
Properties
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)