lsqminnorm

Minimum norm least-squares solution to linear equation

Syntax

X = lsqminnorm(A,B)

X = lsqminnorm(A,B,tol)

X = lsqminnorm(___,rankWarn)

X = lsqminnorm(___,RegularizationFactor=alpha)

Description

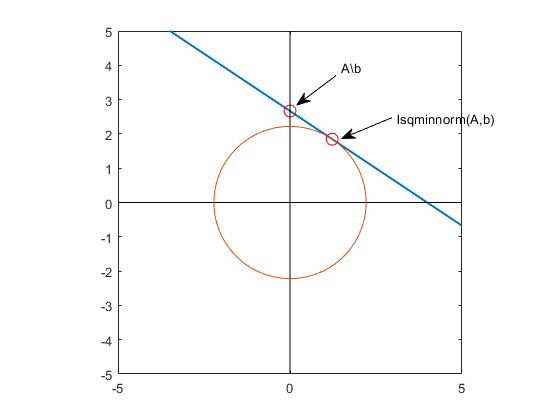
X = lsqminnorm(A,B) returns an array X that solves the linear equation AX = B and minimizes the value of norm(A*X-B). If several solutions exist, then lsqminnorm returns the solution that minimizes norm(X). If B has multiple columns, then the previous statements are true for each column of X and B, respectively.

X = lsqminnorm(A,B,tol) additionally specifies the tolerance that lsqminnorm uses to determine the rank of A.

X = lsqminnorm(___,rankWarn) specifies whether to display a warning if A has low rank. You can specify this option in addition to any of the input argument combinations in previous syntaxes. rankWarn can be "nowarn" (default) or "warn".

X = lsqminnorm(___,RegularizationFactor=alpha) specifies the Tikhonov regularization factor to apply to the solution X. (since R2024b)

Examples

Solve Linear System with Infinite Solutions

Solve a linear system that has infinitely many solutions with backslash (\) and lsqminnorm. Compare the results using the 2-norms of the solutions.

When infinite solutions exist to $\mathrm{Ax}=\mathit{b}$, each of them minimizes $\Vert \mathrm{Ax}-\mathit{b}\Vert$. The backslash command (\) computes one such solution, but this solution typically does not minimize $\Vert \mathit{x}\Vert$. The solution computed by lsqminnorm minimizes not only norm(A*x-b), but also norm(x).

Consider a simple linear system with one equation and two unknowns, $2{\mathit{x}}_1+3{\mathit{x}}_2=8$. This system is underdetermined since there are fewer equations than unknowns. Solve the equation using both backslash and lsqminnorm.

A = [2 3];
b = 8;
x_a = A\b

x_a = 2×1

         0
    2.6667

x_b = lsqminnorm(A,b)

x_b = 2×1

    1.2308
    1.8462

The two methods obtain different solutions because backslash only aims to minimize norm(A*x-b), whereas lsqminnorm also aims to minimize norm(x). Calculate these norms and put the results in a table for easy comparison.

s1 = {'Backslash'; 'lsqminnorm'};
s2 = {'norm_Ax_minus_b','norm_x'};
T = table([norm(A*x_a-b); norm(A*x_b-b)],[norm(x_a); norm(x_b)],'RowNames',s1,'VariableNames',s2)

T=2×2 table
                  norm_Ax_minus_b    norm_x
                  _______________    ______

    Backslash                0       2.6667
    lsqminnorm      8.8818e-16       2.2188

This figure illustrates the situation and shows which solutions each of the methods return. The blue line represents the infinite number of solutions to the equation ${\mathit{x}}_2=-\frac{2}{3}{\mathit{x}}_1+\frac{8}{3}$. The orange circle represents the minimum distance from the origin to the line of solutions, and the solution returned by lsqminnorm lies exactly at the tangent point between the line and circle, indicating it is the solution that is closest to the origin.

Reduce Impact of Noisy Data

You can specify a tolerance for the rank computation or a Tikhonov regularization factor for the solution in lsqminnorm. These specifications help define the scale of the problem so that random noise does not corrupt the solution.

Create a low-rank matrix A of rank 5 and a right-side vector b.

U = randn(200,5);
V = randn(100,5);
A = U*V';
b = U*randn(5,1) + 1e-4*randn(200,1);

Solve the linear system $\mathrm{Ax}=\mathit{b}$ using lsqminnorm. Compute the norms of A*x-b and x to check the quality of the solution.

x = lsqminnorm(A,b);
norm(A*x-b)

ans = 
0.0014

norm(x)

ans = 
0.1741

Now add a small amount of noise to the matrix A and solve the linear system again. The noise affects the solution vector x of the linear system disproportionately.

Anoise = A + 1e-12*randn(200,100);
xnoise = lsqminnorm(Anoise,b);
norm(Anoise*xnoise - b)

ans = 
0.0010

norm(xnoise)

ans = 
1.1215e+08

The reason for the big difference in the solutions is that the noise affects the low-rank approximation of A. In other words, lsqminnorm treats small values on the diagonal of the R matrix in the QR decomposition of A as more important than they actually are. Ideally, these small values on the diagonal of R are treated as zeros.

Plot the diagonal elements of the R matrix in the QR decomposition of Anoise. A large number of the diagonal elements are on the order of 1e-10.

[Q,R,p] = qr(Anoise,0);
semilogy(abs(diag(R)),"o")

Increase the tolerance used by lsqminnorm so that a low-rank approximation of Anoise with error less than 1e-8 is used in the calculation. An increased tolerance makes the result much less susceptible to the noise. The solution using a tolerance is very close to the original solution x.

xtol = lsqminnorm(Anoise,b,1e-8);
norm(Anoise*xtol - b)

ans = 
0.0014

norm(xtol)

ans = 
0.1741

norm(x - xtol)

ans = 
1.0811e-14

Alternatively, specify a Tikhonov regularization factor of 1. For an ill-conditioned problem, such as one that involves noise, you can specify a regularization factor so that overfitting does not occur.

xreg = lsqminnorm(Anoise,b,RegularizationFactor=1);
norm(Anoise*xreg - b)

ans = 
0.0018

norm(xreg)

ans = 
0.1741

norm(x - xreg)

ans = 
7.9359e-06

Toggle Warnings for Low-Rank Matrices

Solve a linear system involving a low-rank coefficient matrix with warnings turned on.

Create a 3-by-3 matrix that is of rank 2. In this matrix, you can obtain the third column by adding together the first two columns.

A = [1 2 3; 4 5 9; 6 7 13]

A = 3×3

     1     2     3
     4     5     9
     6     7    13

Find the minimum norm least-squares solution to the problem $\mathrm{Ax}=\mathit{b}$, where $\mathit{b}$ is equal to the second column in $\mathit{A}$. Specify the 'warn' flag for lsqminnorm to display a warning if it detects that A is of low rank.

b = A(:,2);
x = lsqminnorm(A,b,'warn')

Warning: Rank deficient, rank = 2, tol =  1.072041e-14.

x = 3×1

   -0.3333
    0.6667
    0.3333

Input Arguments

A — Coefficient matrix

matrix

Coefficient matrix. The coefficient matrix appears in the system of linear equations on the left as Ax = B. The coefficient matrix can be full or sparse.

Data Types: double | single
Complex Number Support: Yes

B — Input array

vector | matrix

Input array, specified as a vector or matrix. B appears in the system of linear equations on the right as Ax = B. If B is a matrix, then each column in the matrix represents a different vector for the right-hand side.

Data Types: double | single
Complex Number Support: Yes

tol — Rank tolerance

nonnegative scalar

Rank tolerance, specified as a nonnegative scalar. Specifying the tolerance can help prevent the solution from being susceptible to random noise in the coefficient matrix. By default, lsqminnorm computes tol based on the QR decomposition of A.

lsqminnorm computes the rank of A as the number of diagonal elements in the R matrix of the QR decomposition [Q,R,p] = qr(A,0) with absolute value larger than tol. If the rank of A is k, then the function forms a low-rank approximation of A by multiplying the first k columns of Q by the first k rows of R. Changing the tolerance affects this low-rank approximation of A.

Example: X = lsqminnorm(A,B,1e-2)

Data Types: double

rankWarn — Warning toggle for low-rank matrices

"nowarn" (default) | "warn"

Warning toggle for low-rank matrices, specified as "nowarn" or "warn". Specify "warn" to indicate that lsqminnorm should produce warnings if the coefficient matrix A is rank deficient.

Example: X = lsqminnorm(A,B,"warn")

alpha — Tikhonov regularization factor

0 (default) | real number

Since R2024b

Tikhonov regularization factor for least-squares solution, specified as a real number. Specifying the regularization factor as alpha returns a solution X that minimizes norm(A*X-B)^2 + alpha^2*norm(X)^2 for each column of X. For ill-conditioned problems, specifying the regularization factor gives preference to solutions with smaller norms.

Data Types: double | single

Tips

• The minimum-norm solution computed by lsqminnorm is of particular interest when several solutions exist. The equation Ax = b has many solutions whenever A is underdetermined (fewer rows than columns) or of low rank.

• lsqminnorm(A,B,tol) is typically more efficient than pinv(A,tol)*B for computing minimum norm least-squares solutions to linear systems. lsqminnorm uses the complete orthogonal decomposition (COD) to find a low-rank approximation of A, while pinv uses the singular value decomposition (SVD). Therefore, the results of pinv and lsqminnorm do not match exactly.

• For sparse matrices, lsqminnorm uses a different algorithm than for dense matrices, and therefore can produce different results.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• Code generation does not support sparse matrix inputs for this function.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™. (since R2024b)

The lsqminnorm function supports GPU array input with these usage notes and limitations:

• Coefficient matrix A must be nonsparse.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2017b

R2025a: Code generation support for regularizationFactor

Code generation supports regularizationFactor as input to lsqminnorm.

R2024b: Apply Tikhonov regularization to least-squares solution

You can specify the Tikhonov regularization factor alpha to return a solution X that minimizes norm(A*X-B)^2 + alpha^2*norm(X)^2 for each column of X.