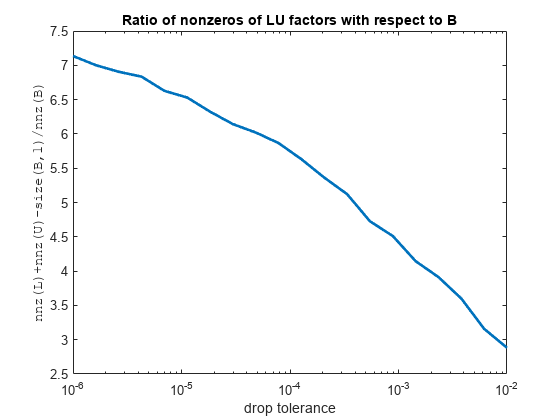
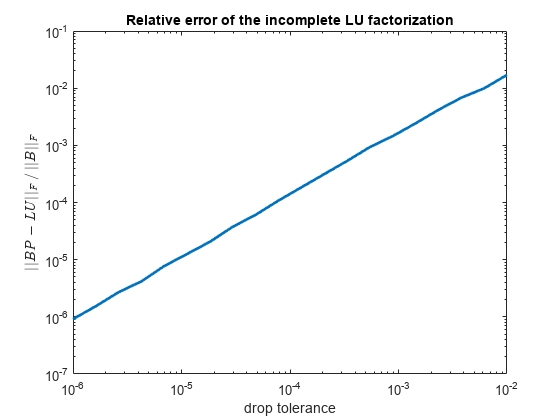
ilu
Incomplete LU factorization
Description
[___] = ilu(
performs the incomplete LU factorization of A,options)A with options specified
by the structure options.
For example, you can perform an incomplete LU factorization with pivoting by setting
the type field of options to
"ilutp". You can then specify a row-sum or column-sum preserving
modified incomplete LU factorization by setting the milu field to
"row" or "col". This combination of options
returns the permutation matrix P such that L and
U are incomplete factors of A*P for the
"row" option (where U is column permuted), or
L and U are incomplete factors of
P*A for the "col" option (where
L is row permuted).
Examples
Input Arguments
Output Arguments
Tips
The incomplete factorizations returned by this function may be useful as preconditioners for a system of linear equations being solved by iterative methods, such as
bicg,bicgstab, orgmres.
References
[1] Saad, Y. "Preconditioning Techniques", chap. 10 in Iterative Methods for Sparse Linear Systems. The PWS Series in Computer Science. Boston: PWS Pub. Co, 1996.