accumarray
Accumulate vector elements
Syntax
Description
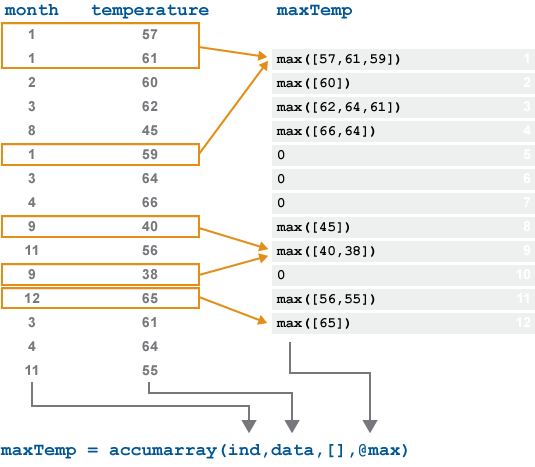
B = accumarray(ind,data)data according to the groups specified in
ind. The sum is then computed over each group. The values in
ind define both the group the data belongs to and the index
into the output array B where each group sum is stored.
To return the group sums in order, specify ind as a vector.
Then for the group with index i, accumarray
returns its sum in B(i). For example, if ind = [1 1 2
2]' and data = [1 2 3 4]', then B =
accumarray(ind,data) returns the column vector B = [3
7]'.
To return the group sums in another shape, specify ind as a
matrix. For an m-by-n matrix
ind, each row represents the group assignment and an
n-dimensional index into the output B. For
example, if ind contains two rows of the form [3
4], then the sum of the corresponding elements in
data is stored in the (3,4) element of
B.
Elements of B whose index does not appear in
ind are filled with 0 by default.
Examples
Input Arguments
Output Arguments
More About
Tips
The behavior of
accumarrayis similar to the functionsgroupsummaryandgroupcountsfor computing summary statistics by group and counting the number of elements in a group, respectively. For more grouping functionality in MATLAB®, see Data Preprocessing.The behavior of
accumarrayis also similar to that of thehistcountsfunction.histcountsgroups continuous values into a 1-D range using bin edges.accumarraygroups data using n-dimensional indices.histcountscan only return bin counts and bin placement.accumarraycan apply any function to the data.
You can mimic the behavior of
histcountsusingaccumarraywithdata = 1.The
sparsefunction also has accumulation behavior similar to that ofaccumarray.sparsegroups data using 2-D indices, whereasaccumarraygroups data using n-dimensional indices.For elements with identical indices,
sparseapplies thesumfunction (fordoublevalues) or theanyfunction (forlogicalvalues) and returns the scalar result in the output matrix.accumarraysums by default, but can apply any function to the data.
Extended Capabilities
Version History
Introduced before R2006a