gradientm
Gradient, slope, and aspect of data grid
Syntax
Description
Regular Data Grids
[
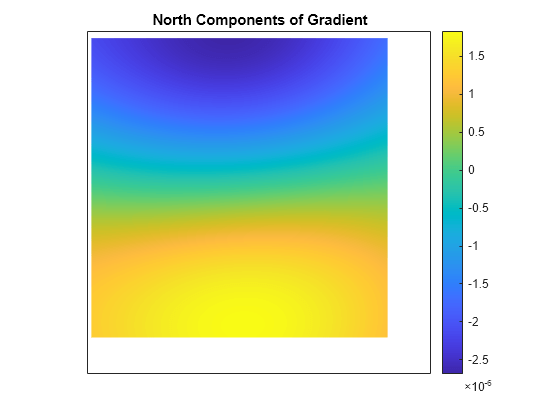
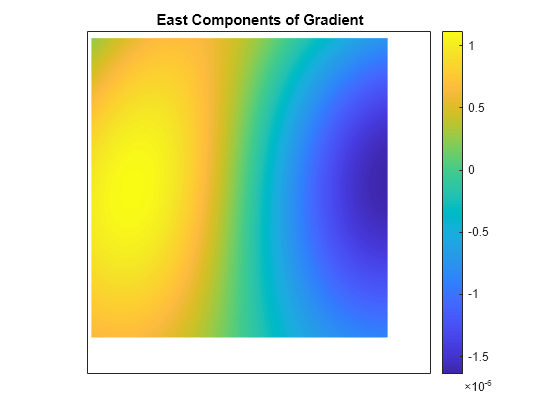
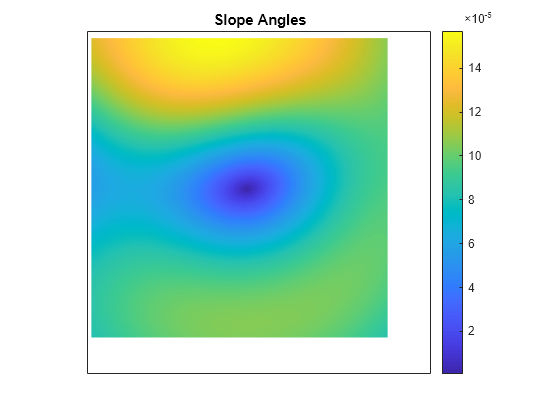
returns the aspect angle, slope angle, and north and east components of the gradient for a
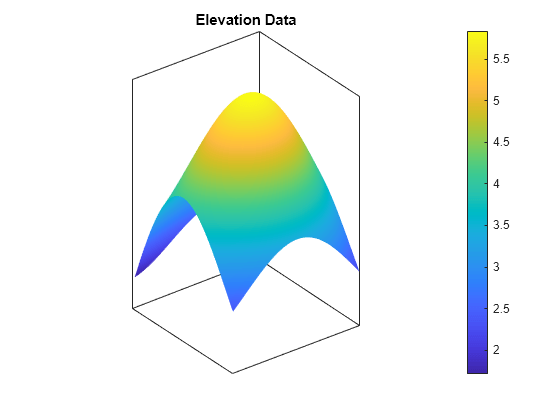
regular data grid aspect,slope,gradN,gradE] = gradientm(F,R)F with respect to a geographic reference
R. By default, gradientm locates the latitude
and longitude coordinates referenced by R using the spheroid
contained in the Spheroid property of the geocrs
object in the GeographicCRS property of R. If
the GeographicCRS property of R is empty, then
geopeaks uses GRS80.