Data Augmentations for Lidar Object Detection Using Deep Learning
This example shows how to perform typical data augmentation techniques for 3-D object detection workflows with lidar data.
Lidar object detection methods predict 3-D bounding boxes around the objects of interest. Data augmentation methods help you avoid overfitting issues while training and also improve the detection accuracy. This example covers global and local augmentation techniques: global augmentation applies to the entire point cloud of a scene and local augmentation techniques applies only to the points belonging to individual objects in a scene.
Load Data
Extract the ZIP file attached to this example to the temp directory. The ZIP file contains sampleWPIPointClouds folder that holds the point clouds and sampleWPILabels.mat file that holds the ground truth labels.
unzip("sampleWPIPointClouds.zip",tempdir); dataLocation = fullfile(tempdir,"sampleWPIPointClouds");
Create a file datastore to load PCD files using the pcread function.
lds = fileDatastore(dataLocation,"ReadFcn",@(x) pcread(x));Create a box label datastore to load the 3-D ground truth bounding boxes.
load("sampleWPILabels.mat","trainLabels") bds = boxLabelDatastore(trainLabels);
Use the combine function to combine the point clouds and 3-D bounding boxes into a single datastore.
cds = combine(lds,bds);
Read the point cloud and corresponding ground truth label from datastore and display.
inputData = read(cds);
ptCloud = inputData{1,1};
gtLabels = inputData{1,2};
figure;
ax = pcshow(ptCloud.Location);Draw the 3-D bounding boxes over the point cloud.
showShape("cuboid",gtLabels,Parent=ax,Opacity=0.1, ... Color="green",LineWidth=0.5); axis on; zoom(ax,2);

reset(cds);
Global Data Augmentation
Global data augmentation techniques are used when the point clouds in a dataset have little variation. A global technique applies transformation to the entire point cloud and generates new point cloud samples. It applies the same transformation to all corresponding ground truth boxes. The following four global data augmentation techniques are commonly used [1].
Random rotation
Random scaling
Random translation
Random flipping
Rotate Point Cloud
Randomly rotate the point cloud and the 3-D bounding boxes within the specified range of angles along the z-axis. By doing so, you can simulate data points, such as a vehicle taking a turn. The typical range for rotation is [-45 45] degrees.
Set the random seed for reproducibility.
rng(1);
Define minimum and maximum yaw angles for rotation.
minYawAngle = -45; maxYawAngle = 45;
Define the grid size to bin the point cloud to.
gridSize = [32 32 32];
Define the limits of the region of interest within the point cloud.
axisLimits = [-100 100];
Create an output view for the affine transformation.
outView = imref3d(gridSize,axisLimits,axisLimits,axisLimits);
Calculate a random angle from the specified yaw angle range.
theta = minYawAngle + rand*(maxYawAngle-minYawAngle);
Create a transformation that rotates the point clouds and 3-D bounding boxes.
tform = randomAffine3d("Rotation",@() deal([0,0,1],theta));
tform = affinetform3d(tform.A);Apply the transformation to the point cloud.
ptCloudTransformed = pctransform(ptCloud,tform);
Apply the same transformation to the 3-D bounding boxes.
gtLabelsTranformed = bboxwarp(gtLabels,tform,outView);
Display the rotated point cloud and the ground truth boxes.
figure; ax1 = pcshow(ptCloudTransformed.Location); showShape("cuboid",gtLabelsTranformed,Parent=ax1,Opacity=0.1, ... Color="green",LineWidth=0.5); axis on; zoom(ax1,2);
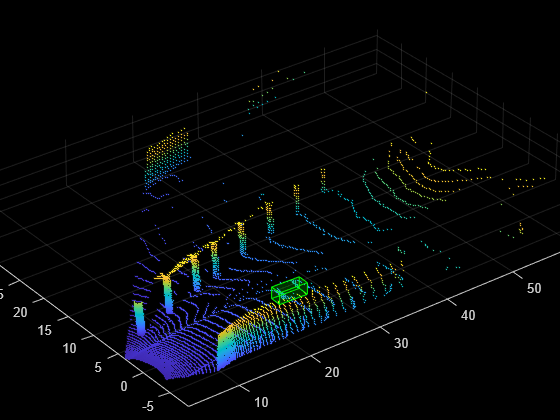
Scale Point Cloud
Randomly scale the point cloud and the 3-D bounding boxes within the specified range of scales. The typical scaling range is [0.95 1.05]. The example uses a range of [0.5 0.7] for better visualization.
Create a transformation to scale the point cloud and 3-D bounding boxes.
tform = randomAffine3d(Scale=[0.5 0.7]); tform = affinetform3d(tform.A);
Apply the transformation to the point cloud.
ptCloudTransformed = pctransform(ptCloud,tform);
Apply the same transformation to the 3-D bounding boxes.
gtLabelsTranformed = bboxwarp(gtLabels,tform,outView);
Display the scaled point cloud and the ground truth boxes.
figure; ax2 = pcshow(ptCloudTransformed.Location); showShape("cuboid",gtLabelsTranformed,Parent=ax2,Opacity=0.1, ... Color="green",LineWidth=0.5); axis on; zoom(ax2,2);

Translate Point Cloud
Randomly translate the point cloud and the 3-D bounding boxes along the x-, y-, and z-axes within the specified range.
Create a transformation to translate the point cloud and 3-D bounding boxes.
tform = randomAffine3d(XTranslation=[0 0.2],... YTranslation=[0 0.2],... ZTranslation=[0 0.1]); tform = affinetform3d(tform.A);
Apply the transformation to the point cloud.
ptCloudTransformed = pctransform(ptCloud,tform);
Apply the same transformation to the 3-D bounding boxes.
gtLabelsTranformed = bboxwarp(gtLabels,tform,outView);
Display the translated point cloud and the ground truth boxes.
figure; ax3 = pcshow(ptCloudTransformed.Location); showShape("cuboid",gtLabelsTranformed,Parent=ax3,Opacity=0.1, ... Color="green",LineWidth=0.5); axis on; zoom(ax3,2);

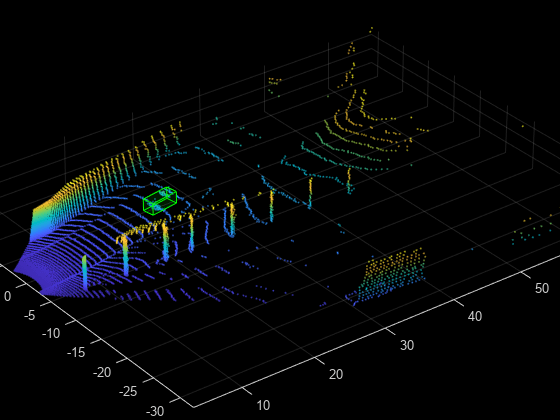
Flip Along Axis
Randomly flip the point cloud and the 3-D bounding boxes along the y-axis. Do not flip along the x-axis, as the bounding box annotations are provided in the camera field of view.
Create a transformation to flip the point cloud and 3-D bounding boxes.
tform = randomAffine3d(YReflection=true); tform = affinetform3d(tform.A);
Apply the transformation to the point cloud.
ptCloudTransformed = pctransform(ptCloud,tform);
Apply the same transformation to the 3-D bounding boxes using the helper function flipBbox, attached to this example as a supporting file.
gtLabels = flipBbox(gtLabels,tform);
Display the flipped point cloud and the ground truth boxes.
figure; ax4 = pcshow(ptCloudTransformed.Location); showShape("cuboid",gtLabels,Parent=ax4,Opacity=0.1, ... Color="green",LineWidth=0.5); axis on; zoom(ax4,2);
Ground Truth Data Augmentation
Ground truth data augmentation is a technique which introduces randomly selected ground truth boxes from a data store or another point cloud into the current point cloud while training [1]. Using this approach, you can increase the number of ground truth boxes per point cloud and simulate objects in different environments. To avoid physically impossible outcomes, you perform a collision test on the samples to be added and the ground truth boxes of the current point cloud. Use this augmentation technique when there is a class imbalance in the data set.
Use the sampleLidarData function to sample 3-D bounding boxes and the corresponding points from a datastore. You can filter out the sampled points using minPoints and store the filtered samples at a location specified by the sampleLocation.
classNames = {'car'};
minPoints = 20;
sampleLocation = fullfile(tempdir,"GTSamples");
[ldsSampled,bdsSampled] = sampleLidarData(cds,classNames,MinPoints=minPoints,...
WriteLocation=sampleLocation,Verbose=false);
cdsSampled = combine(ldsSampled,bdsSampled);Use the pcBboxOversample function to randomly augment a fixed number of objects to the point cloud from the class "car". Define the total number of objects in the output point cloud using totalObjects.
totalObjects = 5; cdsAugmented = transform(cds,@(x)pcBboxOversample(x,cdsSampled,classNames,totalObjects));
Display the point cloud along with the ground truth augmented boxes.
augData = read(cdsAugmented);
augptCld = augData{1,1};
augLabels = augData{1,2};
figure;
ax5 = pcshow(augptCld.Location);
showShape("cuboid",augLabels,Parent=ax5,Opacity=0.1, ...
Color="green",LineWidth=0.5);
axis on;
zoom(ax5,2);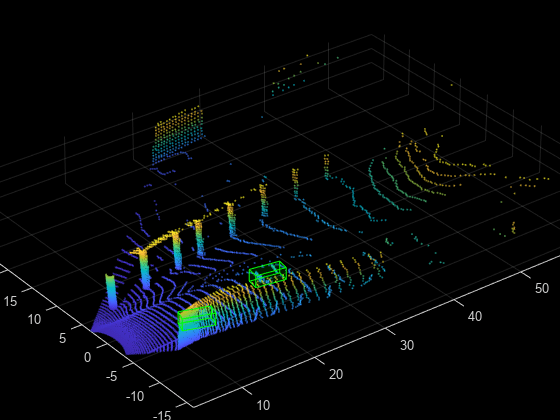
Local Data Augmentation
Local data augmentation applies augmentation only to the points inside the ground truth boxes in a point cloud [1]. The rest of the point cloud remains the same.
Read the point cloud and corresponding ground truth label.
reset(cds);
inputData = read(cds);
ptCloud = inputData{1,1};
gtLabels = inputData{1,2};
gtLabelsTransformed = zeros(size(gtLabels));
for i = 1:size(gtLabels,1)
labelParams = gtLabels(i,:);
centroidLoc = labelParams(1,1:3);
model = cuboidModel(labelParams);
indices = findPointsInModel(model,ptCloud);
numPointsInside = size(indices,1);Segregate the ground truth points from the original point cloud using the helper function removeIndicesFromPointCloud, attached to this example as a supporting file.
updatedPtCloud = removeIndicesFromPtCloud(ptCloud,indices);
cubPtCloud = select(ptCloud,indices);
% Shift the segregated point cloud to the origin.
numPoints = cubPtCloud.Count;
shiftRange = -1.*repmat(centroidLoc,[numPoints 1]);
cubPtCloud = pctransform(cubPtCloud,shiftRange);
% Define the minimum and maximum yaw angles for rotation.
minYawAngle = -45;
maxYawAngle = 45;
% Calculate a random angle from the specified yaw angle range.
theta = minYawAngle + rand*(maxYawAngle - minYawAngle);
% Create a transformation that rotates, translates, and scales the
% point clouds and 3-D bounding boxes.
tform = randomAffine3d("Rotation",@() deal([0 0 1],theta),...
Scale=[0.95 1.05],...
XTranslation=[0 0.2],...
YTranslation=[0 0.2],...
ZTranslation=[0 0.1]);
tform = affinetform3d(tform.A);
% Apply transformation to the 3-D bounding box.
labelParams(1,1:3) = labelParams(1,1:3) - centroidLoc;
labelParamsTransformed = bboxwarp(labelParams,tform,outView);
% Calculate the overlap ratio between the transformed box and the
% original ground truth boxes by converting them to rotated rectangle
% format, defined as [xcenter,ycenter,width,height,yaw].
overlapRatio = bboxOverlapRatio(labelParamsTransformed(:,[1,2,4,5,9]), ...
gtLabels(:,[1,2,4,5,9]));
[maxOverlapRatio, maxOverlapIdx] = max(overlapRatio);
% Check if any transformed boxes overlap with the ground truth
% boxes.
if (maxOverlapRatio > 0) && (maxOverlapIdx ~= i)
shiftRange = -1.*shiftRange;
cubPtCloud = pctransform(cubPtCloud,shiftRange);
updatedPtCloud = pccat([updatedPtCloud,cubPtCloud]);
gtLabelsTransformed(i,1) = labelParams;
else
cubPtCloudTransformed = pctransform(cubPtCloud,tform);
shiftRange = -1.*shiftRange;
cubPtCloudTransformed = pctransform(cubPtCloudTransformed,shiftRange);
updatedPtCloud = pccat([updatedPtCloud,cubPtCloudTransformed]);
gtLabelsTransformed(i,:) = labelParamsTransformed;
end
gtLabelsTransformed(i,1:3) = gtLabelsTransformed(i,1:3) + centroidLoc;
ptCloud = updatedPtCloud;
endDisplay the point cloud along with the augmented ground truth boxes.
figure; ax6 = pcshow(updatedPtCloud.Location); showShape("cuboid",gtLabelsTransformed,Parent=ax6,Opacity=0.1, ... Color="green",LineWidth=0.5); axis on; zoom(ax6,2);

reset(cds);
References
[1] Hahner, Martin, Dengxin Dai, Alexander Liniger, and Luc Van Gool. "Quantifying Data Augmentation for LiDAR Based 3D Object Detection." Preprint, submitted April 3, 2020. https://arxiv.org/abs/2004.01643.
See Also
sampleLidarData | pcBboxOversample | imref3d | affinetform3d | pctransform