spectralMatch
Identify unknown regions or materials using spectral library
Syntax
Description
score = spectralMatch(libData,reflectance,wavelength)reflectance and wavelength, with the values
available in the ECOSTRESS spectral library libData.
score = spectralMatch(___,Name=Value)
Note
This function requires the Hyperspectral Imaging Library for Image Processing Toolbox™. You can install the Hyperspectral Imaging Library for Image Processing Toolbox from Add-On Explorer. For more information about installing add-ons, see Get and Manage Add-Ons.
The Hyperspectral Imaging Library for Image Processing Toolbox requires desktop MATLAB®, as MATLAB Online™ and MATLAB Mobile™ do not support the library.
Examples
The spectral matching method compares the spectral signature of each pixel in the hyperspectral data cube with a reference spectral signature for vegetation from an ECOSTRESS spectrum file.
Read the spectral signature of vegetation from the ECOSTRESS spectral library.
filename = "vegetation.tree.tsuga.canadensis.vswir.tsca-1-47.ucsb.asd.spectrum.txt";
libData = readEcostressSig(filename);Read the hyperspectral data into the workspace.
hcube = imhypercube("paviaU.hdr");Compute the distance scores of the spectrum of the hyperspectral data pixels with respect to the reference spectrum.
score = spectralMatch(libData,hcube);
Display the distance scores. The pixels with low distance scores are stronger matches to the reference spectrum and are more likely to belong to the vegetation region.
imagesc(score) colorbar
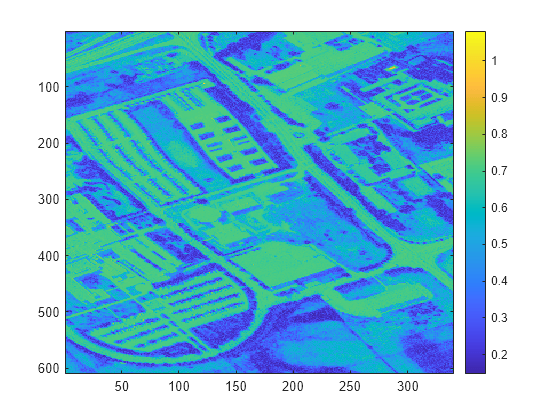
Define a threshold for detecting distance scores that correspond to the vegetation region.
threshold = 0.3;
Create a binary image by applying the threshold. The regions in the binary image with a value of 1 correspond to the vegetation regions in the data cube with distance scores less than the threshold. All other pixels have a value 0.
bw = score < threshold;
Segment the vegetation regions of the hyperspectral data cube by using the indices of the maximum intensity regions in the binary image.
datacube = gather(hcube); T = reshape(datacube,[size(datacube,1)*size(datacube,2) size(datacube,3)]); Ts = zeros(size(T)); Ts(bw == 1,:) = T( bw==1 ,:); Ts = reshape(Ts,[size(datacube,1) size(datacube,2) size(datacube,3)]);
Create a new hypercube object that contains only the segmented vegetation regions.
segmentedDataCube = imhypercube(Ts,hcube.Wavelength);
Estimate the RGB color image of the original data cube and the segmented data cube by using the colorize function.
rgbImg = colorize(hcube,Method="rgb",ContrastStretching=true); segmentedImg = colorize(segmentedDataCube,Method="rgb",ContrastStretching=true);
Overlay the binary image on the RGB version of the original data cube by using the imoverlay function.
B = imoverlay(rgbImg,bw,"Yellow");Display the RGB color images of the original data cube and the segmented data cube along with the overlaid image. The segmented image contains only the vegetation regions that are segmented from the original data cube.
figure
montage({rgbImg,segmentedImg,B},Size=[1 3])
title("Original Image | Segmented Image | Overlaid Image")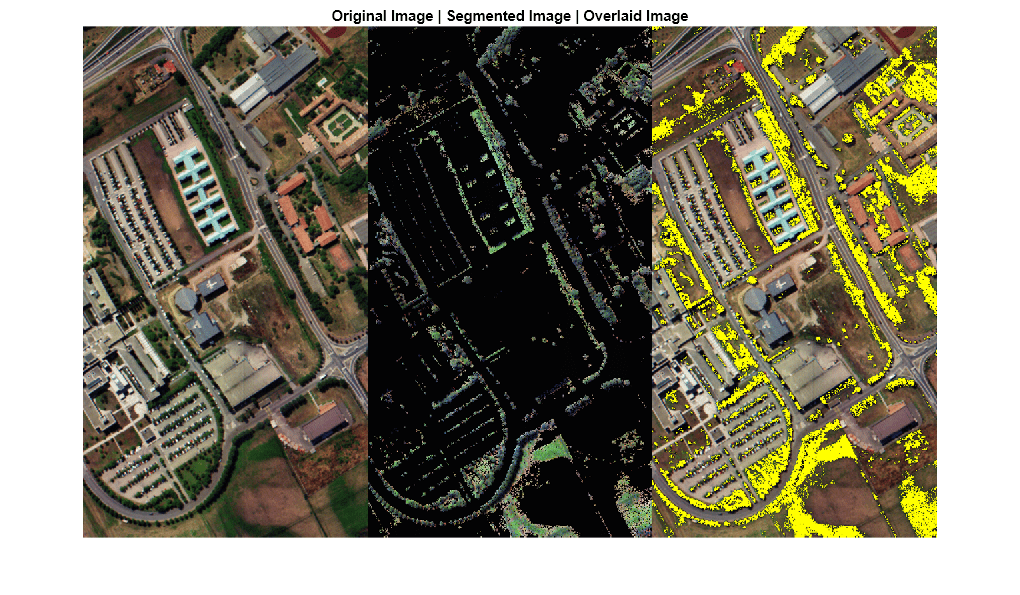
Read reference spectral signatures from the ECOSTRESS spectral library. The library consists of 15 spectral signatures belonging to manmade materials, soil, water, and vegetation. The output is a structure array that stores the spectral data read from ECOSTRESS library files.
dirname = fullfile(matlabroot,"toolbox","images","supportpackages","hyperspectral","hyperdata","ECOSTRESSSpectraFiles"); libData = readEcostressSig(dirname);
Load a .mat file that contains the reflectance and the wavelength values of an unknown material into the workspace. The reflectance and the wavelength values together comprise the test spectrum.
load spectralData.mat reflectance wavelength
Compute the spectral match between the reference spectrum and test spectrum using spectral information divergence (SID) method. The function computes the distance score for only those reference spectra that have bandwidth overlap with the test spectrum. The function displays a warning message for all other spectra. You can turn off the warning messages.
warning off score = spectralMatch(libData,reflectance,wavelength,Method="SID");
Display the distance scores of the test spectrum. The pixels with lower distance scores are stronger matches to the reference spectrum. A distance score value of NaN indicates that the corresponding reference spectrum and the test spectrum do not meet the overlap bandwidth threshold.
score
score = 1×15
297.8016 122.5567 203.5864 103.3351 288.7747 275.5321 294.2341 NaN NaN 290.4887 NaN 299.5762 171.6919 46.2072 176.6637
Find the minimum distance score and the corresponding index. The returned index value indicates the row of the structure array libData that contains the reference spectrum that most closely matches a test spectrum.
[value,ind] = min(score);
Find the matching reference spectrum by using the index of the minimum distance score, and display the details of the matching spectral data in the ECOSTRESS library. The result shows that the test spectrum match most closely with the spectral signature of sea water.
matchingSpectra = libData(ind)
matchingSpectra = struct with fields:
Name: "Sea Foam"
Type: "Water"
Class: "Sea Water"
SubClass: "none"
ParticleSize: "Liquid"
Genus: [0×0 string]
Species: [0×0 string]
SampleNo: "seafoam"
Owner: "Dept. of Earth and Planetary Science, John Hopkins University"
WavelengthRange: "TIR"
Origin: "JHU IR Spectroscopy Lab."
CollectionDate: "N/A"
Description: "Sea foam water. Original filename FOAM Original ASTER Spectral Library name was jhu.becknic.water.sea.none.liquid.seafoam.spectrum.txt"
Measurement: "Directional (10 Degree) Hemispherical Reflectance"
FirstColumn: "X"
SecondColumn: "Y"
WavelengthUnit: "micrometer"
DataUnit: "Reflectance (percent)"
FirstXValue: "14.0112"
LastXValue: "2.0795"
NumberOfXValues: "2110"
AdditionalInformation: "none"
Wavelength: [2110×1 double]
Reflectance: [2110×1 double]
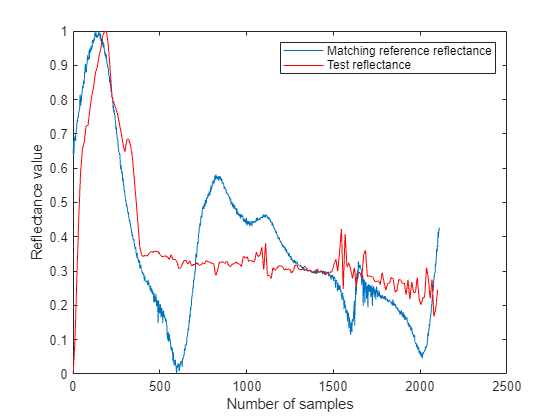
Plot the reflectance values of the test spectrum and the corresponding reference spectrum. For the purpose of plotting and visualizing the shape of the reflectance curves, rescale the reflectance values to the range [0, 1] and interpolate test reflectance values to match the reference reflectance values in number.
figure testReflectance = rescale(reflectance,0,1); refReflectance = rescale(matchingSpectra.Reflectance,0,1); testLength = length(testReflectance); newLength = length(testReflectance)/length(refReflectance); testReflectance = interp1(1:testLength,testReflectance,1:newLength:testLength); plot(refReflectance) hold on plot(testReflectance,"r") hold off legend("Matching reference reflectance","Test reflectance") xlabel("Number of samples") ylabel("Reflectance value")
Input Arguments
Spectral data from spectral library, specified as a structure or a
1-by-K structure array. K is the number of
spectral signatures from the library to be used for spectral matching. Each spectral
library structure must contain Reflectance and
Wavelength fields consisting of numeric vectors of equal length,
such as a spectral signature read from the ECOSTRESS library using the readEcostressSig function.
Input hyperspectral data, specified as a hypercube object.
Reflectance values, specified as a C-element vector. C is the number of wavelengths for which the reflectance values have been measured.
Wavelength values, specified as a C-element vector. C is the number of wavelengths for which the reflectance values have been measured.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: spectralMatch(libData,hcube,MinBandWidth=0.5)
Spectral matching method, specified as one of these values:
"sam"— Spectral angle mapper (SAM) method, which measures the similarity between two spectra by computing the angular distance between them."sid"— Spectral information divergence (SID) method, which measures the similarity between two spectra by computing the difference between their probability distribution values."sidsam"— Mixed spectral similarity method, which measures the similarity between two spectra by combining the SID and SAM distance measures."jmsam"— Jeffries Matusita-Spectral Angle Mapper (JMSAM), which measures the similarity between two spectra by combining the Jeffries Matusita (JM) and SAM distance measures."ns3"— Normalized spectral similarity score (NS3) method, which measures the similarity between two spectra by combining the Euclidean and SAM distance measures.
For details about these spectral matching methods, see Algorithm.
Data Types: char | string
Minimum overlap bandwidth, specified as a positive scalar in nanometers. The overlap bandwidth between the reference spectrum and the test spectra is defined as:
BWoverlap = Wmax − Wmin
Wmin is the maximum of minimum wavelengths in the reference and test spectra.
Wmax is the maximum of maximum wavelengths in the reference and test spectra.
The MinBandWidth argument defines the minimum expected value
for the overlap bandwidth between the spectral values of the test material and the
ECOSTRESS spectral data.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Output Arguments
Distance scores, returned as a 3-D numeric array, matrix,
K-element column vector, or scalar. The dimensions of the output
score depend on the dimensions of the libData and whether the test
data is a hypercube object or a wavelength and
reflectance pair.
If the test spectral signatures are specified as a hypercube
object, hcube and the data cube is of size
M-by-N-by-C:
Dimension of input argument,
libData | Dimension of output,
score |
| 1-by-K, containing K reference signatures read from K number of spectrum files | 3-D numeric array of size M-by-N-by-K containing the distance score for each pixel with respect to K reference signatures The values in each
channel of K are the distance scores of the spectra of
each pixel with respect to the spectral data in the corresponding row of
|
| 1-by-1, containing reference signature read from one spectrum file (K = 1) | matrix of size M-by-N, The matrix contains the distance score for each pixel's spectra with respect to a reference signature. |
If the test spectral signature is specified as reflectance
and wavelength values:
Dimension of input argument,
libData | Dimension of output,
score |
| 1-by-K, containing K reference signatures read from K number of spectrum files | K-element vector containing the distance score of the
test spectra with respect to K reference signatures. Each
element of the vector is the distance score of the test reflectance values
with respect to the spectral data in the corresponding row of
libData. |
| 1-by-1, containing reference signature read from one spectrum file (K = 1) | scalar |
Data Types: double
Limitations
This function does not support parfor loops when the Method is specified as
"sam", "sid", "jmsam", or
"ns3", as its performance is already optimized. (since R2023a)
Algorithms
For the "sam" method, the spectralMatch function
computes the SAM score α using this formula.
where, r and t are the reference and test spectra, respectively. ri and ti are the ith elements of the vectors r and t, respectively. C is the length of vectors r and t.
For the "sid" method, the spectralMatch function
normalizes the reference spectra refSpectra and test spectra
testSpectra and computes the SID value using this formula.
q and p are the vectors of normalized reference and test spectra, respectively. qi and pi are the ith elements of the vectors q and p, respectively. C is the length of vectors q and p.
For the "sidsam" method, the
spectralMatch function computes the SID-SAM value using this formula.
SID is the SID value, and α is the SAM score.
For the "jmsam" method, the
spectralMatch function computes the JMSAM score using this formula.
JMdistance is the JM distance, and α is the SAM score. This method computes the JM distance using this formula.
B is the Bhattacharyya distance:
μr and μt are the mean values of the reference and test spectra, respectively. σr and σt are the covariance values of the reference and test spectra, respectively.
For the "ns3" method, the
spectralMatch function computes the NS3 score using this formula.
AEuclidean is the Euclidean distance, and α is the SAM score. This method computes the Euclidean distance using this formula.
r and t are the vectors of reference and test spectra, respectively. ri and ti are the ith elements of the vectors r and t, respectively. C is the length of vectors r and t.
Version History
Introduced in R2020a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)