fsamp2
2-D FIR filter using frequency sampling
Description
h = fsamp2(Hd)Hd,
and returns the filter coefficients in matrix h. The filter
h has a frequency response that passes through points in
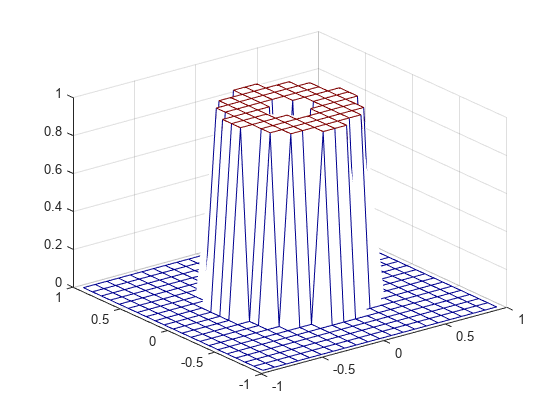
Hd. fsamp2 designs two-dimensional FIR
filters based on a desired two-dimensional frequency response sampled at points on
the Cartesian plane.
h = fsamp2(f1,f2,Hd,[m n])m-by-n FIR filter by matching the
filter response at the points in the vectors f1 and
f2. The frequency vectors f1 and
f2 are in normalized frequency, where 1.0 corresponds to half
the sampling frequency, or π radians. The resulting filter fits the desired response
as closely as possible in the least squares sense. For best results, there must be
at least m*n desired frequency points. fsamp2
issues a warning if you specify fewer than m*n points.
Examples
Input Arguments
Output Arguments
Algorithms
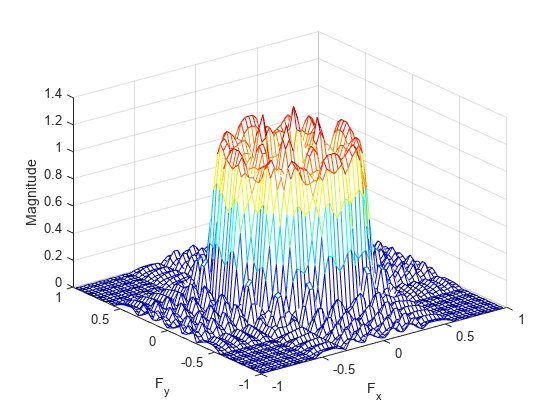
fsamp2 computes the filter h by taking the
inverse discrete Fourier transform of the desired frequency response. If the desired
frequency response is real and symmetric (zero phase), the resulting filter is also zero
phase.
References
[1] Lim, Jae S., Two-Dimensional Signal and Image Processing, Englewood Cliffs, NJ, Prentice Hall, 1990, pp. 213-217.
Version History
Introduced before R2006a