bwlookup
Nonlinear filtering using lookup tables
Syntax
Description
A = bwlookup(BW,lut)BW. The neighborhood processing determines an integer index value
used to access values in lookup table lut. The fetched
lut value becomes the pixel value in output image
A at the targeted position.
Examples
Construct a lookup table lut such that the filtering operation places a 1 at the targeted pixel location in the input image only when all four pixels in the 2-by-2 neighborhood of BW are set to 1.
lutfun = @(x)(sum(x(:))==4); lut = makelut(lutfun,2);
Load a binary image.
BW1 = imread("text.png");Perform 2-by-2 neighborhood processing with 16-element vector lut.
BW2 = bwlookup(BW1,lut);
Display the original and eroded image.
h1 = subplot(1,2,1); imshow(BW1); title("Original Image") h2 = subplot(1,2,2); imshow(BW2); title("Eroded Image")

Zoom in to see the effects of erosion on the text.
set(h1,Ylim=[1 64],Xlim=[1 64]); set(h2,Ylim=[1 64],Xlim=[1 64]);

Input Arguments
Binary image to be transformed by the nonlinear neighborhood filtering operation,
specified as a 2-D logical matrix or 2-D numeric matrix. For numeric input,
any nonzero pixels are considered to be 1 (true).
Lookup table of output pixel values, specified as a 16- or 512-element vector. The size of
lut determines which of the two neighborhood operations is
performed. You can use the makelut function to create a lookup
table.
If
lutcontains 16 data elements, then the neighborhood matrix is 2-by-2.If
lutcontains 512 data elements, then the neighborhood matrix is 3-by-3.
Output Arguments
Algorithms
The bwlookup function performs these steps to determine the value of
each pixel in the processed image A:
Locate the pixel neighborhood in input image
BWbased on the coordinates of the target pixel inA. The function zero-pads border pixels of imageBWwhen the neighborhood extends past the edge ofBW.Calculate an index,
idx, based on the binary pixel pattern of the neighborhood.Set the target pixel in
Aas the value of the lookup table at the indexidx, in other words, the value oflut(idx).
For an example that demonstrates each step of the algorithm, see Look Up Value of Sample Pixel.
For 2-by-2 neighborhoods, there are four pixels in each neighborhood. Each binary pixel
has two possible states, therefore the total number of permutations is
24 and the length of the lookup table lut
is 16.
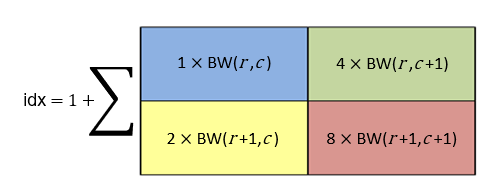
To find the value of the target output pixel at (row, column) coordinate
(r,c), bwlookup uses the 2-by-2
pixel neighborhood in the input binary image BW whose top left pixel is
at coordinate (r,c). The index idx
into the lookup table is the weighted sum of the four pixels in the neighborhood, plus
1.
For 3-by-3 neighborhoods, there are nine pixels in each neighborhood. Each binary pixel
has two possible states, therefore the total number of permutations is
29 and the length of the lookup table lut
is 256.
To find the value of the target output pixel at (row, column) coordinate
(r,c), bwlookup uses the 3-by-3
pixel neighborhood in the input binary image BW centered on coordinate
(r,c). The index idx into the
lookup table is the weighted sum of the nine pixels in the neighborhood, plus 1.
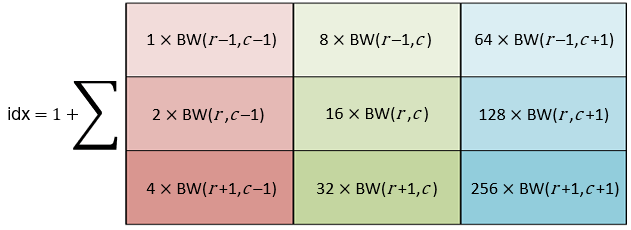
This example shows how to determine the index into a lookup table for a target pixel based on the 2-by-2 neighborhood of the pixel.
Create a random 16-element lookup table. Set the random seed so that the results are reproducible.
rng("default")
lut = randperm(16)lut = 1×16
6 3 16 11 7 14 8 5 15 1 2 4 13 9 10 12
Create a small sample binary image.
BW = checkerboard(2,1,1)>0.5
BW = 4×4 logical array
0 0 1 1
0 0 1 1
1 1 0 0
1 1 0 0
Assume for this example that the targeted pixel location is location BW(2,1). Find the 2-by-2 neighborhood of the target pixel.
targetRow = 2; targetColumn = 1; neighborhood = BW(targetRow:targetRow+1,targetColumn:targetColumn+1)
neighborhood = 2×2 logical array
0 0
1 1
Calculate the index into the lookup table.
idx = 1 + 1*neighborhood(1,1) + 2*neighborhood(2,1) ...
+ 4*neighborhood(1,2) + 8*neighborhood(2,2)idx = 11
Alternatively, you can represent the neighborhood as a binary string and convert the string to an index using the bin2dec function. Create the string by listing the values of the neighborhood in the order (2,2), (2,1), (1,2), (1,1). In other words, the value of neighborhood(2,2) contributes to the most significant bit, which comes first in the string. The value of neighborhood(1,1) contributes to the least significant bit, which comes last in the string.
binStr = "1 0 1 0";
idx = 1 + bin2dec(binStr)idx = 11
Calculate the value of the target pixel by finding the value of the lookup table at the index idx.
targetPixelValue = lut(idx)
targetPixelValue = 2
The above calculation predicts that output image A should contain the value 2 at the target position A(2,1). Confirm the prediction by performing the 2-by-2 nonlinear neighborhood filtering operation on the original binary image BW.
A = bwlookup(BW,lut)
A = 4×4
6 13 12 11
2 8 14 3
12 11 6 6
14 3 6 6
Extended Capabilities
Usage notes and limitations:
bwlookupsupports the generation of C code (requires MATLAB® Coder™). Note that if you choose the genericMATLAB Host Computertarget platform,bwlookupgenerates code that uses a precompiled, platform-specific shared library. Use of a shared library preserves performance optimizations but limits the target platforms for which code can be generated. For more information, see Types of Code Generation Support in Image Processing Toolbox.When generating code, specify an input image of class
logical.
Usage notes and limitations:
When generating code, specify an input image of class
logical.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
This function fully supports GPU arrays. For more information, see Image Processing on a GPU.
Version History
Introduced in R2012bbwlookup now supports thread-based
environments.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)