Perform Simple 2-D Translation Transformation
This example shows how to perform a simple affine transformation called a translation. In a translation, you shift an image in coordinate space by adding a specified value to the x- and y-coordinates. (You can also use the imtranslate function to perform translation.)
Read the image to be transformed. This example creates a checkerboard image using the checkerboard function.
cb = checkerboard; imshow(cb)

Get spatial referencing information about the image. This information is useful when you want to display the result of the transformation.
cb_ref = imref2d(size(cb))
cb_ref =
imref2d with properties:
XWorldLimits: [0.5000 80.5000]
YWorldLimits: [0.5000 80.5000]
ImageSize: [80 80]
PixelExtentInWorldX: 1
PixelExtentInWorldY: 1
ImageExtentInWorldX: 80
ImageExtentInWorldY: 80
XIntrinsicLimits: [0.5000 80.5000]
YIntrinsicLimits: [0.5000 80.5000]
Specify the amount of translation in the x and y directions.
tx = 20; ty = 30;
Create a transltform2d geometric transformation object that represents the translation transformation. For other types of geometric transformations, you can use other types of objects.
tform = transltform2d(tx,ty);
Perform the transformation. Call the imwarp function, specifying the image you want to transform and the geometric transformation object. imwarp returns the transformed image, cb_translated. This example also returns the optional spatial referencing object, cb_translated_ref, which contains spatial referencing information about the transformed image.
[cb_translated,cb_translated_ref] = imwarp(cb,tform);
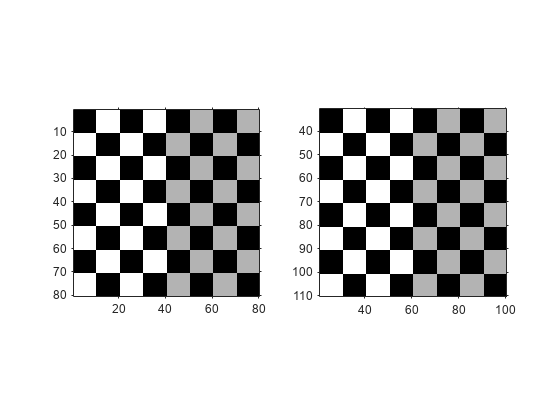
View the original and the transformed image side-by-side. When viewing the translated image, it might appear that the transformation had no effect. The transformed image looks identical to the original image. The reason that no change is apparent in the visualization is because imwarp sizes the output image to be just large enough to contain the entire transformed image but not the entire output coordinate space. Notice, however, that the coordinate values have been changed by the transformation.
figure subplot(1,2,1) imshow(cb,cb_ref) subplot(1,2,2) imshow(cb_translated,cb_translated_ref)
To see the entirety of the transformed image in the same relation to the origin of the coordinate space as the original image, use imwarp with the "OutputView" name-value argument, specifying a spatial referencing object. The spatial referencing object specifies the size of the output image and how much of the output coordinate space is included in the output image. To do this, the example makes a copy of the spatial referencing object associated with the original image and modifies the world coordinate limits to accommodate the full size of the transformed image. The example sets the limits of the output image in world coordinates to include the origin from the input.
cb_translated_ref = cb_ref;
cb_translated_ref.XWorldLimits(2) = cb_translated_ref.XWorldLimits(2)+tx;
cb_translated_ref.YWorldLimits(2) = cb_translated_ref.YWorldLimits(2)+ty;
[cb_translated,cb_translated_ref] = imwarp(cb,tform, ...
OutputView=cb_translated_ref);
figure
subplot(1,2,1)
imshow(cb,cb_ref)
subplot(1,2,2)
imshow(cb_translated,cb_translated_ref);
See Also
imwarp | imref2d | transltform2d | affinetform2d