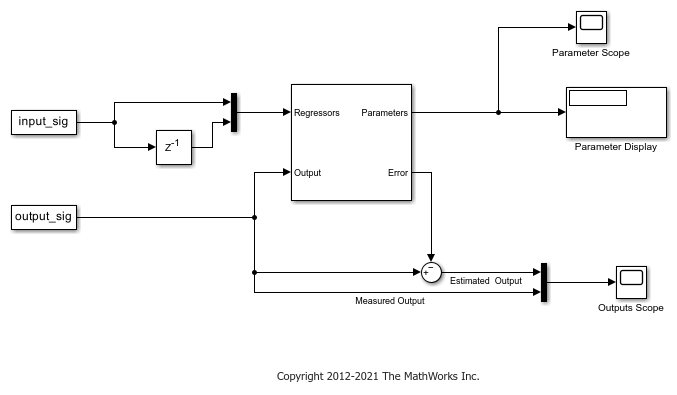
Recursive Least Squares Estimator
Estimate model coefficients using recursive least squares (RLS) algorithm
Libraries:
System Identification Toolbox /
Estimators
Description
The Recursive Least Squares Estimator estimates the parameters of a system using a model that is linear in those parameters. Such a system has the following form:
y and H are known quantities that you provide to the block to estimate θ. The block can provide both infinite-history [1] and finite-history [2] (also known as sliding-window), estimates for θ. For more information on these methods, see Recursive Algorithms for Online Parameter Estimation.
The block supports several estimation methods and data input formats. Configurable options in the block include:
Sample-based or frame-based data format — See the Input Processing parameter.
Infinite-history or finite- history estimation — See the History parameter.
Multiple infinite-history estimation methods — See the Estimation Method parameter.
Initial conditions, enable flag, and reset trigger — See the Initial Estimate, Add enable port, and External Reset parameters.
For a given time step t, y(t) and H(t) correspond to the Output and Regressors inports of the Recursive Least Squares Estimator block, respectively. θ(t) corresponds to the Parameters outport.
For example, suppose that you want to estimate a scalar gain, θ, in the system y = h2θ. Here, y is linear with respect to θ. You can use the Recursive Least Squares Estimator block to estimate θ. Specify y and h2 as inputs to the Output and Regressor inports.
Examples
Online Recursive Least Squares Estimation
Implement an online recursive least squares estimator. You estimate a nonlinear model of an internal combustion engine and use recursive least squares to detect changes in engine inertia.
Estimate Parameters of System Using Simulink Recursive Estimator Block
Use a model containing Simulink recursive estimator to accept input and output signals, construct a regressor signal, and estimate system parameters.
Use Frame-Based Data for Recursive Estimation in Simulink
Use frame-based signals in a Simulink recursive estimation model.
Ports
Input
Regressors input signal H(t). The Input Processing and Number of Parameters parameters define the dimensions of the signal:
Sample-based input processing and N estimated parameters — 1-by-N vector
Frame-based input processing with M samples per frame and N estimated parameters — M-by-N matrix
Data Types: single | double
Measured output signal y(t). The Input Processing parameter defines the dimensions of the signal:
Sample-based input processing — Scalar
Frame-based input processing with M samples per frame — M-by-1 vector
Data Types: single | double
External signal that allows you to enable and disable estimation updates. If the signal value is:
true— Estimate and output the parameter values for the time step.false— Do not estimate the parameter values, and output the most recent previously estimated value.
Dependencies
To enable this port, select the Add enable port parameter.
Data Types: single | double | Boolean | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32
Reset parameter estimation to its initial conditions. The value of the External reset parameter determines the trigger type. The trigger type dictates whether the reset occurs on a signal that is rising, falling, either rising or falling, level, or on level hold.
Dependencies
To enable this port, select any option other than
None in the External reset
dropdown.
Data Types: single | double | Boolean | int8 | int16 | int32 | uint8 | uint16 | uint32
Initial parameter estimates, supplied from a source external to the block. The block uses this inport at the beginning of the simulation or when you trigger an algorithm reset using the Reset signal.
The Number of Parameters parameter defines the dimensions of the signal. If there are N parameters, the signal is N-by-1.
Dependencies
To enable this port, set History to
Infinite and Initial Estimate to
External.
Data Types: single | double
Initial parameter covariances, supplied from a source external to the block. For details, see the Parameter Covariance Matrix parameter. The block uses this inport at the beginning of the simulation or when you trigger an algorithm reset using the Reset signal.
Dependencies
To enable this port, set the following parameters:
History to
InfiniteEstimation Method to
Forgetting FactororKalman FilterInitial Estimate to
External
Data Types: single | double
Initial values of the regressors in the initial data window when using finite-history (sliding-window) estimation, supplied from an external source. The Window length parameter W and the Number of Parameters parameter N define the dimensions of this signal, which is W-by-N.
The InitialRegressors signal controls the initial behavior of the algorithm. The block uses this inport at the beginning of the simulation or whenever the Reset signal triggers.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
Dependencies
To enable this port, set History to
Finite and Initial Estimate to
External.
Data Types: single | double
Initial set of output measurements when using finite-history (sliding-window) estimation, supplied from an external source. The signal to this port must be a W-by-1 vector, where W is the window length.
The InitialOutputs signal controls the initial behavior of the algorithm. The block uses this inport at the beginning of the simulation or whenever the Reset signal triggers.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
Dependencies
To enable this port, set History to
Finite, and Initial Estimate to
External.
Data Types: single | double
Output
Estimated parameters θ(t), returned as an N-by-1 vector where N is the number of parameters.
Data Types: single | double
Estimation error, returned as:
Scalar — Sample-based input processing
M-by-1 vector — Frame-based input processing with M samples per frame
Dependencies
To enable this port, select the Output estimation error parameter.
Data Types: single | double
Parameter estimation error covariance P, returned as an N-by-N matrix, where N is the number of parameters. For details, see the Output Parameter Covariance Matrix parameter.
Dependencies
To enable this port:
If History is
Infinite, set Estimation Method toForgetting FactororKalman Filter.Whether History is
InfiniteorFinite, select the Output parameter covariance matrix parameter.
Data Types: single | double
Parameters
Model Parameters
Specify how to provide initial parameter estimates to the block:
None— Do not specify initial estimates.If History is
Infinite, the block uses1as the initial parameter estimate.If History is
Finite, the block calculates the initial parameter estimates from the initial Regressors and Outputs signals.
Specify Number of Parameters, and also, if History is
Infinite, Parameter Covariance Matrix.Internal— Specify initial parameter estimates internally to the blockIf History is
Infinite, specify the Initial Parameter Values and Parameter Covariance Matrix parameters.If History is
Finite, specify the Number of Parameters, the Initial Regressors, and the Initial Outputs parameters.
External— Specify initial parameter estimates as an input signal to the block.Specify the Number of Parameters parameter. Your setting for the History parameter determines which additional signals to connect to the relevant ports:
If History is
Infinite— InitialParameters and InitialCovarianceIf History is
Finite— InitialRegressors and InitialOutputs
Programmatic Use
Block Parameter:
InitialEstimateSource |
| Type: character vector, string |
Values: 'None',
'Internal', 'External' |
Default: 'None' |
Specify the number of parameters to estimate in the model, equal to the number of elements in the parameter θ(t) vector.
Dependencies
To enable this parameter, set either:
History to
Infiniteand Initial Estimate to eitherNoneorExternalHistory to
Finite
An alternative way to specify the number of parameters N to
estimate is by using the Initial Parameter Values parameter,
for which you define an initial estimate vector with N elements.
This approach covers the one remaining combination, where
History is Infinite and
Initial Estimate is Internal. For
more information, see Initial Parameter Values.
Programmatic Use
Block Parameter:
InitialParameterData |
| Type: positive integer |
Default: 2 |
Specify Parameter Covariance Matrix as a:
Real positive scalar, α — Covariance matrix is an N-by-N diagonal matrix, with α as the diagonal elements.
Vector of real positive scalars, [α1,...,αN] — Covariance matrix is an N-by-N diagonal matrix, with [α1,...,αN] as the diagonal elements.
N-by-N symmetric positive-definite matrix.
Here, N is the number of parameters to be estimated.
Dependencies
To enable this parameter, set the following parameters:
History to
InfiniteInitial Estimate to
NoneorInternalEstimation Method to
Forgetting FactororKalman Filter
Programmatic Use
Block Parameter:
P0 |
| Type: scalar, vector, or matrix |
Default: 1e4 |
Specify initial parameter values as a vector of length N, where N is the number of parameters to estimate.
Dependencies
To enable this parameter, set History to
Infinite and Initial Estimate to
Internal.
Programmatic Use
Block Parameter:
InitialParameterData |
| Type: real vector |
Default: [1 1] |
Specify the initial values of the regressors buffer when using finite-history (sliding window) estimation. The Window length parameter W and the Number of Parameters parameter N define the dimensions of the regressors buffer, which is W-by-N.
The Initial Regressors parameter controls the initial behavior of the algorithm. The block uses this parameter at the beginning of the simulation or whenever the Reset signal triggers.
When the initial value is set to 0, the block populates the
buffer with zeros.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
Dependencies
To enable this parameter, set History to
Finite and Initial Estimate to
Internal.
Programmatic Use
Block Parameter:
InitialRegressors |
| Type: real matrix |
Default: 0 |
Specify initial values of the measured outputs buffer when using finite-history (sliding-window) estimation. This parameter is a W-by-1 vector, where W is the window length.
When the initial value is set to 0, the block populates the
buffer with zeros.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation.
The warning should clear after a few cycles. The number of cycles it takes for
sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, you should evaluate the content of your
signals.
The Initial Outputs parameter controls the initial behavior of the algorithm. The block uses this parameter at the beginning of the simulation or whenever the Reset signal triggers.
Dependencies
To enable this parameter, set History to
Finite and Initial Estimate to
Internal.
Programmatic Use
Block Parameter:
InitialOutputs |
| Type: real vector |
Default: 0 |
Input Processing and Sample Time
Sample-basedprocessing operates on signals streamed one sample at a time.Frame-basedprocessing operates on signals containing samples from multiple time steps. Many machine sensor interfaces package multiple samples and transmit these samples together in frames.Frame-basedprocessing allows you to input this data directly without having to first unpack it.
Specifying frame-based data adds an extra dimension of M to some of your data inports and outports, where M is the number of time steps in a frame. These ports are:
Regressors
Output
Error
For more information, see the port descriptions in Ports.
Programmatic Use
Block Parameter:
InputProcessing |
| Type: character vector, string |
Values: 'Sample-based',
'Frame-based' |
Default:
'Sample-based' |
Specify the data sample time, whether by individual samples for sample-based processing (ts), or by frames for frame-based processing (tf = Mts), where M is the frame length. When you set Sample Time to its default value of -1, the block inherits its ts or tf based on the signal.
Specify Sample Time as a positive scalar to override the inheritance.
Programmatic Use
Block Parameter:
Ts |
| Type: real scalar |
Default: -1 |
Algorithm and Block Options
Algorithm Options
The History parameter determines what type of recursive algorithm you use:
Infinite— Algorithms in this category aim to produce parameter estimates that explain all data since the start of the simulation. These algorithms retain the history in a data summary. The block maintains this summary within a fixed amount of memory that does not grow over time.The block provides multiple algorithms of the
Infinitetype. Selecting this option enables the Estimation Method parameter with which you specify the algorithm.Finite— Algorithms in this category aim to produce parameter estimates that explain only a finite number of past data samples. The block uses all of the data within a finite window, and discards data once that data is no longer within the window bounds. This method is also called sliding-window estimation.Selecting this option enables the Window Length parameter that sizes the sliding window.
For more information on recursive estimation methods, see Recursive Algorithms for Online Parameter Estimation
Programmatic Use
Block Parameter:
History |
| Type: character vector, string |
Values: 'Infinite',
'Finite' |
Default:
'Infinite' |
The Window Length parameter determines the number of time samples to use for the sliding-window estimation method. Choose a window size that balances estimation performance with computational and memory burden. Sizing factors include the number and time variance of the parameters in your model. Always specify Window Length in samples, even if you are using frame-based input processing.
Window Length must be greater than or equal to the number of estimated parameters.
Suitable window length is independent of whether you are using sample-based or frame-based input processing. However, when using frame-based processing, Window Length must be greater than or equal to the number of samples (time steps) contained in the frame.
Dependencies
To enable this parameter, set History to
Finite.
Programmatic Use
Block Parameter:
WindowLength |
| Type: positive integer |
Default: 200 |
Specify the estimation algorithm when performing infinite-history estimation. When you select any of these methods, the block enables additional related parameters.
Forgetting factor and Kalman filter algorithms are more computationally intensive than gradient and normalized gradient methods. However, these more intensive methods have better convergence properties than the gradient methods. For more information about these algorithms, see Recursive Algorithms for Online Parameter Estimation.
Programmatic Use
Block Parameter:
EstimationMethod |
| Type: character vector, string |
Values: 'Forgetting
Factor','Kalman Filter','Normalized
Gradient','Gradient' |
Default: 'Forgetting
Factor' |
The forgetting factor λ specifies if and how much old data is discounted in the estimation. Suppose that the system remains approximately constant over T0 samples. You can choose λ such that:
Setting λ = 1 corresponds to “no forgetting” and estimating constant coefficients.
Setting λ < 1 implies that past measurements are less significant for parameter estimation and can be “forgotten.” Set λ < 1 to estimate time-varying coefficients.
Typical choices of λ are in the [0.98 0.995] range.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Forgetting Factor.
Programmatic Use
Block Parameter:
AdaptationParameter |
| Type: scalar |
| Values: (0 1] range |
Default: 1 |
Process Noise Covariance prescribes the elements and structure of the noise covariance matrix for the Kalman filter estimation. Using N as the number of parameters to estimate, specify the Process Noise Covariance as one of the following:
Real nonnegative scalar, α — Covariance matrix is an N-by-N diagonal matrix, with α as the diagonal elements.
Vector of real nonnegative scalars, [α1,...,αN] — Covariance matrix is an N-by-N diagonal matrix, with [α1,...,αN] as the diagonal elements.
N-by-N symmetric positive semidefinite matrix.
The Kalman filter algorithm treats the parameters as states of a dynamic system and estimates these parameters using a Kalman filter. Process Noise Covariance is the covariance of the process noise acting on these parameters. Zero values in the noise covariance matrix correspond to constant coefficients, or parameters. Values larger than 0 correspond to time-varying parameters. Use large values for rapidly changing parameters. However, expect the larger values to result in noisier parameter estimates. The default value is 1.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Kalman Filter.
Programmatic Use
Block Parameter:
AdaptationParameter |
| Type: scalar, vector, matrix |
Default: 1 |
The adaptation gain γ scales the influence of new measurement data on the estimation results for the gradient and normalized gradient methods. When your measurements are trustworthy, or in other words have a high signal-to-noise ratio, specify a larger value for γ. However, setting γ too high can cause the parameter estimates to diverge. This divergence is possible even if the measurements are noise free.
When Estimation Method is
NormalizedGradient, Adaptation Gain
should be less than 2. With either gradient method, if errors are growing in time (in
other words, estimation is diverging), or parameter estimates are jumping around
frequently, consider reducing Adaptation Gain.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Normalized Gradient or to
Gradient.
Programmatic Use
Block Parameter:
AdaptationParameter |
| Type: scalar |
Default: 1 |
The normalized gradient algorithm scales the adaptation gain at each step by the square of the two-norm of the gradient vector. If the gradient is close to zero, the near-zero denominator can cause jumps in the estimated parameters. Normalization Bias is the term introduced to the denominator to prevent these jumps. Increase Normalization Bias if you observe jumps in estimated parameters.
Dependencies
To enable this parameter, set History to
Infinite and Estimation Method to
Normalized Gradient.
Programmatic Use
Block Parameter:
NormalizationBias |
| Type: scalar |
Default: eps |
Block Options
Use the Error outport signal to validate the estimation. For a given time step t, the estimation error e(t) is calculated as:
where y(t) is the measured output that you provide, and yest(t) is the estimated output using the regressors H(t) and parameter estimates θ(t-1).
Programmatic Use
Block Parameter:
OutputError |
| Type: character vector, string |
Values:
'off','on', |
Default: 'off' |
Use the Covariance outport signal to examine parameter
estimation uncertainty. The software computes parameter covariance
P assuming that the residuals,
e(t), are white noise, and the variance of
these residuals is 1.
The interpretation of P depends on the estimation approach you
specify in History and Estimation Method as follows:
If History is
Infinite, then your Estimation Method selection results in:Forgetting Factor— (R2/2)Pis approximately equal to the covariance matrix of the estimated parameters, where R2 is the true variance of the residuals. The block outputs the residuals in the Error port.Kalman Filter— R2Pis the covariance matrix of the estimated parameters, and R1 /R2 is the covariance matrix of the parameter changes. Here, R1 is the covariance matrix that you specify in Parameter Covariance Matrix.Normalized GradientorGradient— Covariance P is not available.
If History is
Finite(sliding-window estimation) — R2 P is the covariance of the estimated parameters. The sliding-window algorithm does not use this covariance in the parameter-estimation process. However, the algorithm does compute the covariance for output so that you can use it for statistical evaluation.
Programmatic Use
Block Parameter:
OutputP |
| Type: character vector, string |
Values:
'off','on' |
Default: 'off' |
Use the Enable signal to provide a control signal that enables or disables parameter estimation. The block estimates the parameter values for each time step that parameter estimation is enabled. If you disable parameter estimation at a given step, t, then the software does not update the parameters for that time step. Instead, the block outputs the last estimated parameter values.
You can use this option, for example, when or if:
Your regressors or output signal become too noisy, or do not contain information at some time steps
Your system enters a mode where the parameter values do not change in time
Programmatic Use
Block Parameter:
AddEnablePort |
| Type: character vector, string |
Values:
'off','on' |
Default: 'off' |
Set the External reset parameter to both add a Reset inport and specify the inport signal condition that triggers a reset of algorithm states to their specified initial values. Reset the estimation, for example, if parameter covariance is becoming too large because of lack of either sufficient excitation or information in the measured signals.
Suppose that you reset the block at a time step, t. If the block is enabled at t, the software uses the initial parameter values specified in Initial Estimate to estimate the parameter values. In other words, at t, the block performs a parameter update using the initial estimate and the current values of the inports.
If the block is disabled at t and you reset the block, the block outputs the values specified in Initial Estimate.
Specify this option as one of the following:
None— Algorithm states and estimated parameters are not reset.Rising— Trigger reset when the control signal rises from a negative or zero value to a positive value. If the initial value is negative, rising to zero triggers reset.Falling— Trigger reset when the control signal falls from a positive or a zero value to a negative value. If the initial value is positive, falling to zero triggers reset.Either— Trigger reset when the control signal is either rising or falling.Level— Trigger reset in either of these cases:Control signal is nonzero at the current time step.
Control signal changes from nonzero at the previous time step to zero at the current time step.
Level hold— Trigger reset when the control signal is nonzero at the current time step.
When you choose any option other than None, the
software adds a Reset inport to the block. You provide the reset control input signal
to this inport.
Programmatic Use
Block Parameter:
ExternalReset |
| Type: character vector, string |
Values:
'None','Rising','Falling',
'Either', 'Level', 'Level
hold' |
Default: 'None' |
References
[1] Ljung, L. System Identification: Theory for the User. Upper Saddle River, NJ: Prentice-Hall PTR, 1999, pp. 363–369.
[2] Zhang, Q. "Some Implementation Aspects of Sliding Window Least Squares Algorithms." IFAC Proceedings. Vol. 33, Issue 15, 2000, pp. 763-768.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced in R2014a
See Also
Recursive Polynomial Model Estimator | Kalman Filter
Topics
- Estimate Parameters of System Using Simulink Recursive Estimator Block
- Online Recursive Least Squares Estimation
- Preprocess Online Parameter Estimation Data in Simulink
- Validate Online Parameter Estimation Results in Simulink
- Generate Online Parameter Estimation Code in Simulink
- Recursive Algorithms for Online Parameter Estimation
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)