idnlarx/linearize
Linearize nonlinear ARX model
Syntax
SYS = linearize(NLSYS,U0,X0)
Description
SYS = linearize(NLSYS,U0,X0) linearizes
a nonlinear ARX model about the specified operating point U0 and X0.
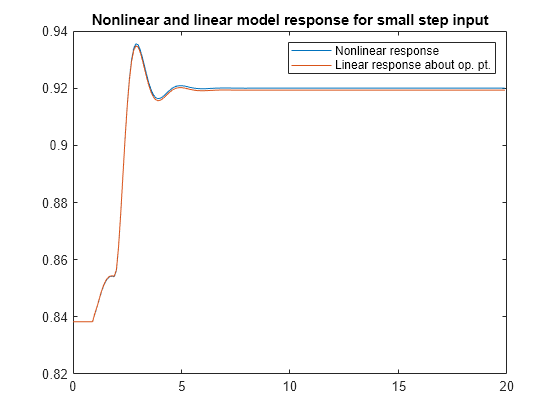
The linearization is based on tangent linearization. For more information
about the definition of states for idnlarx models,
see Definition of idnlarx States.
Input Arguments
NLSYS:idnlarxmodel.U0: Matrix containing the constant input values for the model.X0: Model state values. The states of a nonlinear ARX model are defined by the time-delayed samples of input and output variables. For more information about the states of nonlinear ARX models, see thegetDelayInforeference page.
Note
To estimate U0 and X0 from operating point
specifications, use the idnlarx/findop command.
Output Arguments
SYSis anidssmodel.When the Control System Toolbox™ product is installed,
SYSis an LTI object.
Examples
Algorithms
The following equations govern the dynamics of an idnlarx model:
where X(t) is a state vector, u(t) is the input, and y(t) is the output. A and B are constant matrices. is [y(t), u(t)]T.
The output at the operating point is given by
y* = f(X*, u*)
where X* and u* are the state vector and input at the operating point.
The linear approximation of the model response is as follows:
where
Note
For linear approximations over larger input ranges, use linapp.
Version History
Introduced in R2014b