Constrained Minimization Using ga, Problem-Based

This example shows how to minimize an objective function, subject to nonlinear inequality constraints and bounds, using ga in the problem-based approach. For a solver-based version of this problem, see Constrained Minimization Using the Genetic Algorithm.

Constrained Minimization Problem

For this problem, the fitness function to minimize is a simple function of 2-D variables X and Y.

camxy = @(X,Y)(4 - 2.1.*X.^2 + X.^4./3).*X.^2 + X.*Y + (-4 + 4.*Y.^2).*Y.^2;

This function is described in Dixon and Szego [1].

Additionally, the problem has nonlinear constraints and bounds.

   x*y + x - y + 1.5 <= 0  (nonlinear constraint)
   10 - x*y <= 0           (nonlinear constraint)
   0 <= x <= 1             (bound)
   0 <= y <= 13            (bound)

Plot the nonlinear constraint region on a surface plot of the fitness function. The constraints limit the solution to the small region above both red curves.

x1 = linspace(0,1);
y1 = (-x1 - 1.5)./(x1 - 1);
y2 = 10./x1;
[X,Y] = meshgrid(x1,linspace(0,13));
Z = camxy(X,Y);
surf(X,Y,Z,"LineStyle","none")
hold on
z1 = camxy(x1,y1);
z2 = camxy(x1,y2);
plot3(x1,y1,z1,'r-',x1,y2,z2,'r-')
xlim([0 1])
ylim([0 13])
zlim([0,max(Z,[],"all")])
hold off

Create Optimization Variables, Problem, and Constraints

To set up this problem, create optimization variables x and y. Set the bounds when you create the variables.

x = optimvar("x","LowerBound",0,"UpperBound",1);
y = optimvar("y","LowerBound",0,"UpperBound",13);

Create the objective as an optimization expression.

cam = camxy(x,y);

Create an optimization problem with this objective function.

prob = optimproblem("Objective",cam);

Create the two nonlinear inequality constraints, and include them in the problem.

prob.Constraints.cons1 = x*y + x - y + 1.5 <= 0;
prob.Constraints.cons2 = 10 - x*y <= 0;

Review the problem.

show(prob)

  OptimizationProblem : 

	Solve for:
       x, y

	minimize :
       (((((4 - (2.1 .* x.^2)) + (x.^4 ./ 3)) .* x.^2) + (x .* y)) + (((-4) + (4 .* y.^2)) .* y.^2))


	subject to cons1:
       ((((x .* y) + x) - y) + 1.5) <= 0

	subject to cons2:
       (10 - (x .* y)) <= 0

	variable bounds:
       0 <= x <= 1

       0 <= y <= 13

Solve Problem

Solve the problem, specifying the ga solver.

[sol,fval] = solve(prob,"Solver","ga")

Solving problem using ga.
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

sol = struct with fields:
    x: 0.8122
    y: 12.3103

fval = 
9.1268e+04

Add Visualization

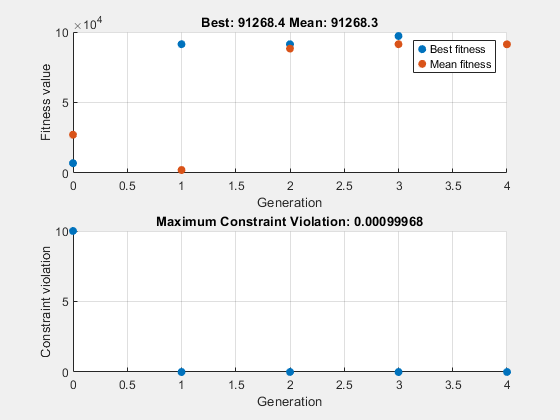
To observe the solver's progress, specify options that select two plot functions. The plot function gaplotbestf plots the best objective function value at every iteration, and the plot function gaplotmaxconstr plots the maximum constraint violation at every iteration. Set these two plot functions in a cell array. Also, display information about the solver's progress in the Command Window by setting the Display option to 'iter'.

options = optimoptions(@ga,...
    'PlotFcn',{@gaplotbestf,@gaplotmaxconstr},...
    'Display','iter');

Run the solver, including the options argument.

[sol,fval] = solve(prob,"Solver","ga","Options",options)

Solving problem using ga.

Single objective optimization:
2 Variables
2 Nonlinear inequality constraints

Options:
CreationFcn:       @gacreationuniform
CrossoverFcn:      @crossoverscattered
SelectionFcn:      @selectionstochunif
MutationFcn:       @mutationadaptfeasible

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2520       91357.8            0      0
    2           4982       91324.1     4.55e-05      0
    3           7914       97166.6            0      0
    4          16145       91268.4    0.0009997      0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

sol = struct with fields:
    x: 0.8123
    y: 12.3103

fval = 
9.1268e+04

Nonlinear constraints cause ga to solve many subproblems at each iteration. As shown in both the plots and the iterative display, the solution process has few iterations. However, the Func-count column in the iterative display shows many function evaluations per iteration.

Unsupported Functions

If your objective or nonlinear constraint functions are not supported (see Supported Operations for Optimization Variables and Expressions), use fcn2optimexpr to convert them to a form suitable for the problem-based approach. For example, suppose that instead of the constraint $$xy\ge 10$$, you have the constraint $$I_1(x)+I_1(y)\ge 10$$, where $$I_1(x)$$ is the modified Bessel function besseli(1,x). (The Bessel functions are not supported functions.) Create this constraint using fcn2optimexpr. First, create an optimization expression for $$I_1(x)+I_1(y)$$.

bfun = fcn2optimexpr(@(t,u)besseli(1,t) + besseli(1,u),x,y);

Next, replace the constraint cons2 with the constraint bfun >= 10.

prob.Constraints.cons2 = bfun >= 10;

Solve the problem. The solution is different because the constraint region is different.

[sol2,fval2] = solve(prob,"Solver","ga","Options",options)

Solving problem using ga.

Single objective optimization:
2 Variables
2 Nonlinear inequality constraints

Options:
CreationFcn:       @gacreationuniform
CrossoverFcn:      @crossoverscattered
SelectionFcn:      @selectionstochunif
MutationFcn:       @mutationadaptfeasible

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2512       974.044            0      0
    2           4974       960.998            0      0
    3           7436        963.12            0      0
    4          12001        960.83    0.0009335      0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

sol2 = struct with fields:
    x: 0.4999
    y: 3.9979

fval2 = 
960.8300

References

[1] Dixon, L. C. W., and G .P. Szego (eds.). Towards Global Optimisation 2. North-Holland: Elsevier Science Ltd., Amsterdam, 1978.