Nonlinear System Identification Using ANFIS
This example shows how to perform dynamic system identification by using a linear ARX and a nonlinear ANFIS model.
Load Data
The data set used in this example for ANFIS and ARX modeling is from a "Feedback's Process Trainer PT 326" laboratory device [1]. The device functions like a hair dryer: air is fanned through a tube and heated at the inlet. A thermocouple measures the air temperature. The input is the voltage over a mesh of resistor wires to heat incoming air and the output is the outlet air temperature.

Load the test data and plot the input and output.
load dryerdata data_n = length(y); output = y; input = [[0; y(1:data_n-1)] ... [0; 0; y(1:data_n-2)] ... [0; 0; 0; y(1:data_n-3)] ... [0; 0; 0; 0; y(1:data_n-4)] ... [0; u(1:data_n-1)] ... [0; 0; u(1:data_n-2)] ... [0; 0; 0; u(1:data_n-3)] ... [0; 0; 0; 0; u(1:data_n-4)] ... [0; 0; 0; 0; 0; u(1:data_n-5)] ... [0; 0; 0; 0; 0; 0; u(1:data_n-6)]]; data = [input output]; data(1:6,:) = []; input_name = ["y(k-1)","y(k-2)","y(k-3)","y(k-4)",... "u(k-1)","u(k-2)","u(k-3)","u(k-4)","u(k-5)","u(k-6)"]; index = 1:100; figure subplot(2,1,1) plot(index,y(index),"-",index,y(index),"o") title("Output Data") ylabel("y(k)") subplot(2,1,2) plot(index,u(index),"-",index,u(index),"o") title("Input Data") ylabel("u(k)")
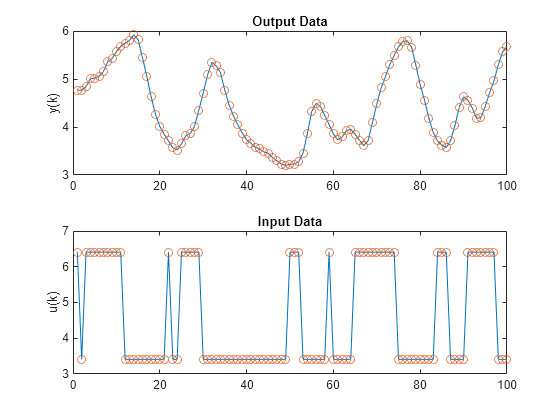
The data points reflect a sample time of 0.08 seconds. The input is a binary random signal shifting between 3.41 and 6.41. The probability of shifting the input at each sample is 0.2. The data set contains 1000 input/output data points. These plots show the output temperature and input voltage for the first 100 time steps.
Identify ARX Model
An ARX model is a linear model of the following form:
Here:
and are mean-subtracted versions of the original data.
and are linear parameters.
, , and are three integers that exactly specify the ARX model.
To find an ARX model for the dryer device, first divide the data set into a training ( = 1 to 300) and a validation ( = 301 to 600) set.
trn_data_n = 300; total_data_n = 600; z = [y u]; z = dtrend(z); ave = mean(y); ze = z(1:trn_data_n,:); zv = z(trn_data_n+1:total_data_n,:); T = 0.08;
Perform an exhaustive search to find the best combination of , , and , allowing each integer to change from 1 to 10 independently. To perform the search and select the ARX parameters, use the arxstruc (System Identification Toolbox) and selstruc (System Identification Toolbox) functions.
% Run through all different models. V = arxstruc(ze,zv,struc(1:10,1:10,1:10)); % Find the best model. nn = selstruc(V,0); % Display model parameters disp("[m n d] = " + num2str(nn))
[m n d] = 5 10 2
The best ARX model has = 5, = 10, and = 2. Create with a training root mean squared error (RMSE) of 0.1122 and a validation RMSE of 0.0749. Plot the original along with this ARX model.
Create and simulate an ARX model with these parameters.
th = arx(ze,nn); th.Ts = 0.08; u = z(:,2); y = z(:,1) + ave; yp = sim(u,th) + ave;
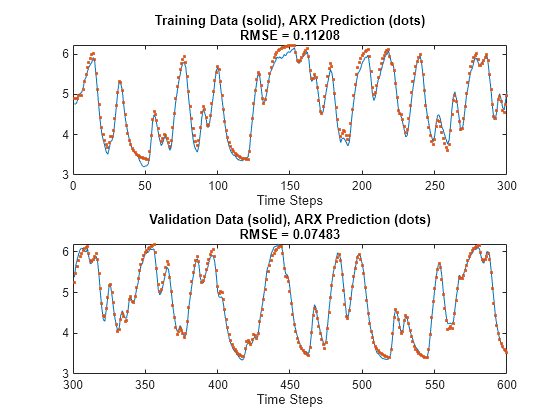
Plot the ARX model output against the training and validation data. The training root mean squared error (RMSE) is 0.1121 and the validation RMSE is 0.0748.
figure subplot(2,1,1) index = 1:trn_data_n; plot(index,y(index),index,yp(index), '.') rmse = norm(y(index)-yp(index))/sqrt(length(index)); title("Training Data (solid), ARX Prediction (dots)" ... + newline + "RMSE = " + num2str(rmse)) xlabel("Time Steps") subplot(2,1,2) index = (trn_data_n+1):(total_data_n); plot(index,y(index),index,yp(index),'.') rmse = norm(y(index)-yp(index))/sqrt(length(index)); title("Validation Data (solid), ARX Prediction (dots)" ... + newline + "RMSE = " + num2str(rmse)) xlabel("Time Steps")
Identify ANFIS Model
The ARX model is linear and can perform model structure and parameter identification rapidly. The performance in the previous plots appears to be satisfactory. However, if you want better performance, you can try a nonlinear model such as an adaptive neuro-fuzzy inference system (ANFIS).
To use an ANFIS for system identification, first determine which variables to use for the input arguments. For simplicity, use 10 input candidates (, , , , , , , , , and ). Use as the output.
Perform a sequential forward search of the inputs using the function sequentialSearch. This function selects each input variable sequentially to optimize the RMSE.
trn_data_n = 300; trn_data = data(1:trn_data_n,:); val_data = data(trn_data_n+1:trn_data_n+300,:); [~,elapsed_time] = sequentialSearch(3,trn_data,val_data,input_name);
Selecting input 1 ... Model 1: y(k-1), Error: trn = 0.2043, val = 0.1888 Model 2: y(k-2), Error: trn = 0.3819, val = 0.3541 Model 3: y(k-3), Error: trn = 0.5245, val = 0.4903 Model 4: y(k-4), Error: trn = 0.6308, val = 0.5977 Model 5: u(k-1), Error: trn = 0.8271, val = 0.8434 Model 6: u(k-2), Error: trn = 0.7976, val = 0.8087 Model 7: u(k-3), Error: trn = 0.7266, val = 0.7349 Model 8: u(k-4), Error: trn = 0.6215, val = 0.6346 Model 9: u(k-5), Error: trn = 0.5419, val = 0.5650 Model 10: u(k-6), Error: trn = 0.5304, val = 0.5601 Currently selected inputs: y(k-1) Selecting input 2 ... Model 11: y(k-1) y(k-2), Error: trn = 0.1085, val = 0.1024 Model 12: y(k-1) y(k-3), Error: trn = 0.1339, val = 0.1283 Model 13: y(k-1) y(k-4), Error: trn = 0.1542, val = 0.1461 Model 14: y(k-1) u(k-1), Error: trn = 0.1892, val = 0.1734 Model 15: y(k-1) u(k-2), Error: trn = 0.1663, val = 0.1574 Model 16: y(k-1) u(k-3), Error: trn = 0.1082, val = 0.1077 Model 17: y(k-1) u(k-4), Error: trn = 0.0925, val = 0.0948 Model 18: y(k-1) u(k-5), Error: trn = 0.1533, val = 0.1531 Model 19: y(k-1) u(k-6), Error: trn = 0.1952, val = 0.1853 Currently selected inputs: y(k-1) u(k-4) Selecting input 3 ... Model 20: y(k-1) u(k-4) y(k-2), Error: trn = 0.0808, val = 0.0822 Model 21: y(k-1) u(k-4) y(k-3), Error: trn = 0.0806, val = 0.0836 Model 22: y(k-1) u(k-4) y(k-4), Error: trn = 0.0817, val = 0.0855 Model 23: y(k-1) u(k-4) u(k-1), Error: trn = 0.0886, val = 0.0912 Model 24: y(k-1) u(k-4) u(k-2), Error: trn = 0.0835, val = 0.0843 Model 25: y(k-1) u(k-4) u(k-3), Error: trn = 0.0609, val = 0.0604 Model 26: y(k-1) u(k-4) u(k-5), Error: trn = 0.0848, val = 0.0867 Model 27: y(k-1) u(k-4) u(k-6), Error: trn = 0.0890, val = 0.0894 Currently selected inputs: y(k-1) u(k-3) u(k-4)

This plot shows all combinations of inputs tried by sequentialSearch. The search selects , , and as inputs since the model with these inputs has the lowest training RMSE and validation RMSE.
Alternatively, you can use an exhaustive search on all possible combinations of the input candidates. As before, search for three inputs out of the 10 candidates. You can use the function exhaustiveSearch for such a search; however, this function tries all possible combinations of candidates, in this case.
Instead of exhaustiveSearch, use custom code to search through a subset of these combinations. For this example, do not select any input combination exclusively from the inputs or exclusively from the outputs.
As a reasonable guess, select input combinations with two output values and one input value, which produces 36 possible input combinations. Define groups for selecting input indices: two groups for selecting an output and one group for selecting an input.
group1 = [1 2 3 4]; % y(k-1), y(k-2), y(k-3), y(k-4) group2 = [1 2 3 4]; % y(k-1), y(k-2), y(k-3), y(k-4) group3 = [5 6 7 8 9 10]; % u(k-1) through u(k-6)
Specify parameters and options for training.
anfis_n = 6*length(group3); index = zeros(anfis_n,3); trn_error = zeros(anfis_n,1); val_error = zeros(anfis_n,1); % Create option set for generating initial FIS. genOpt = genfisOptions("GridPartition", ... NumMembershipFunctions=2, ... InputMembershipFunctionType="gbellmf"); % Create option set for anfis function and set options that remain % constant for different training scenarios. anfisOpt = anfisOptions( ... EpochNumber=1,... InitialStepSize=0.1,... StepSizeDecreaseRate=0.5,... StepSizeIncreaseRate=1.5,... DisplayANFISInformation=0,... DisplayErrorValues=0,... DisplayStepSize=0,... DisplayFinalResults=0);
Train ANFIS model for each input combination.
model = 1; for i = 1:length(group1) for j = i+1:length(group2) for k = 1:length(group3) % Create input combinations. in1 = input_name(group1(i)); in2 = input_name(group2(j)); in3 = input_name(group3(k)); index(model, :) = [group1(i) group2(j) group3(k)]; trn_data = data(1:trn_data_n, ... [group1(i) group2(j) group3(k) size(data,2)]); val_data = data(trn_data_n+1:trn_data_n+300, ... [group1(i) group2(j) group3(k) size(data,2)]); % Create the initial FIS structure. in_fis = genfis(trn_data(:,1:end-1),trn_data(:,end),genOpt); % Set the initial FIS and validation data for ANFIS training. anfisOpt.InitialFIS = in_fis; anfisOpt.ValidationData = val_data; % Train the ANFIS system. [~,t_err,~,~,c_err] = anfis(trn_data,anfisOpt); trn_error(model) = min(t_err); val_error(model) = min(c_err); model = model+1; end end end
Plot the training and validation errors for each input combination in decreasing order.
% Reorder according to training error. [~, b] = sort(trn_error); b = flipud(b); trn_error = trn_error(b); val_error = val_error(b); index = index(b,:); % Plot training and validation error. x = (1:anfis_n)'; tmp = x(:, ones(1,3))'; X = tmp(:); tmp = [zeros(anfis_n,1) max(trn_error,val_error) nan*ones(anfis_n,1)]'; Y = tmp(:); figure plot(x,trn_error,"-o",x,val_error,"-*",X,Y,"g") title("Error for Corresponding Inputs") ylabel("RMSE") legend("Training","Validation",Location="northeast") % Add ticks and labels. labels = string(zeros(anfis_n,1)); for k = 1:anfis_n labels(k) = input_name(index(k,1))+ " & " + ... input_name(index(k,2))+ " & " + ... input_name(index(k,3)); end xticks(x) xticklabels(labels) xtickangle(90)

The algorithm selects the inputs , , and with a training RMSE of 0.0474 and a validation RMSE of 0.0485. These RMSE values improve on those of the ARX models and that of the ANFIS model found by sequential forward search.
Compute and plot the ANFIS predictions for both the training and validation data sets using the selected input combination.
To do so, first generate the data set.
[~,b] = min(trn_error); input_index = index(b,:); trn_data = data(1:trn_data_n,[input_index, size(data,2)]); val_data = data(trn_data_n+1:600,[input_index, size(data,2)]);
Create and train the ANFIS.
in_fis = genfis(trn_data(:,1:end-1),trn_data(:,end)); anfisOpt = anfisOptions( ... InitialFIS=in_fis,... EpochNumber=1,... InitialStepSize=0.01,... StepSizeDecreaseRate=0.5,... StepSizeIncreaseRate=1.5,... ValidationData=val_data); [trn_out_fis,trn_error,step_size,val_out_fis,val_error] = ... anfis(trn_data,anfisOpt);
ANFIS info: Number of nodes: 34 Number of linear parameters: 32 Number of nonlinear parameters: 18 Total number of parameters: 50 Number of training data pairs: 300 Number of checking data pairs: 300 Number of fuzzy rules: 8 Start training ANFIS ... 1 0.0474113 0.0485325 Designated epoch number reached. ANFIS training completed at epoch 1. Minimal training RMSE = 0.0474113 Minimal checking RMSE = 0.0485325
Evaluate the FIS for which the validation error is minimum.
y_hat = evalfis(val_out_fis,data(1:600,input_index)); figure subplot(2,1,1) index = 1:trn_data_n; plot(index,data(index,size(data,2)),'-', ... index,y_hat(index),'.') rmse = norm(y_hat(index)-data(index,size(data,2)))/sqrt(length(index)); title("Training Data (solid), ANFIS Prediction (dots)" ... + newline + "RMSE = " + num2str(rmse)) xlabel("Time Steps") subplot(2,1,2) index = trn_data_n+1:600; plot(index,data(index,size(data,2)),'-',index,y_hat(index),'.') rmse = norm(y_hat(index)-data(index,size(data,2)))/sqrt(length(index)); title("Validation Data (solid), ANFIS Prediction (dots)" ... + newline + "RMSE = " + num2str(rmse)) xlabel("Time Steps")

The ANFIS model predictions fit the data much more closely than the ARX model predictions.
Reference
[1] Ljung, Lennart. System Identification: Theory for the User. Prentice-Hall Information and System Sciences Series. Englewood Cliffs, NJ: Prentice-Hall, 1987.