Systolic QR Decomposition

QR decomposition for matrices

Since R2024a

• 

×

Libraries:
Fixed-Point Designer HDL Support / Matrices and Linear Algebra / Matrix Factorizations

Description

The Systolic QR Decomposition block uses QR decomposition to compute R and C = Q'B, where QR = A, and A and B are matrices. The least-squares solution to AX = B is X = R\C. R is an upper triangular matrix and Q is an orthogonal matrix. To compute C = Q', set B to be the identity matrix.

The systolic implementation to minimizes system latency and increases the throughput. Systolic implementations require more hardware resources than burst or partial-systolic implementations.

Examples

How to Use Systolic QR Decomposition Block

This example shows how to use the Systolic QR Decomposition block to compute the QR decomposition.

Economy Size QR Decomposition

The Systolic QR Decomposition block performs the first step of solving the least-squares matrix equation AX = B which transforms A in-place to R and B in-place to C = Q'B, then solves the transformed system RX = C, where QR is the orthogonal-triangular decomposition of A.

To compute the standalone QR decomposition, this example sets B to be the identity matrix so that the output of the Systolic QR Decomposition block is the upper-triangular R and C = Q'. For more information, see Systolic QR Decomposition.

I/O interface

This block uses the AMBA AXI handshake protocol on both the input and the output side. On the input side, data transaction occurs when both validIn and ready signals are asserted. On the output side, data transaction occurs when both validOut and readyIn signals are asserted.

In this example, the validIn and readyIn signals remain asserted which indicates the upstream source and downstream sink are always available. When all matrices A and B are sent, the Data Handler loops back to the first A and B matrices.

Define Block Parameters

Specify the dimension of the sample matrices A and B, the number of input sample matrices, and the complexity of matrices A and B.

The Systolic QR Decomposition block supports both real and complex inputs. Set the complexity of the input in the block mask accordingly.

m = 3;
n = 3;
p = m;
numSamples = 3;
Complexity = "real";

Generate Input Matrices A and B

Use the specified simulation parameters to generate the input matrices A and B.

rng('default');
if strcmp(Complexity,'real')
    A = 2*(rand(m,n,numSamples)-0.5);
    B = repmat(eye(m),[1,1,numSamples]);
else
    A = complex(2*(rand(m,n,numSamples)-0.5),...
        2*(rand(m,n,numSamples)-0.5));
    B = complex(repmat(eye(m),[1,1,numSamples]));
end

Define and Cast to Input Data Type

Specify a data type for the inputs, and cast the inputs to that data type.

DT = "fixed";

For fixed-point data types, define the number of precision bits.

precisionBits = 18;

Cast the inputs to the selected data type.

T = fixed.qrFixedpointTypes(m,max(abs(A(:))),max(abs(B(:))),precisionBits);
tv = castToDT(A,B,T,DT);

Open Model and Run Simulation

Open the FullSystolicQRModel model. Configure the model workspace and run the simulation.

model = 'FullSystolicQRModel';
open_system(model);

fixed.example.setModelWorkspace(model,'A',tv.A,'B',tv.B,...
    'm',m,'n',n,'p',p,'OutputType',tv.OutputType,'numSamples',numSamples);
dutName = [model '/Systolic QR Decomposition'];
set_param(dutName,'complexity',Complexity);
out = sim(model);

Verify Output Solutions

The Systolic QR Decomposition block computes C = Q'B. In this example, B is the identity matrix, so Q = C' is the economy-size orthogonal factor of the QR decomposition.

R_actual = out.R;
C_actual = out.C;

To verify the solutions output by the model, check that

• Q is orthogonal within round-off error,

• R is an upper-triangular matrix, and

• QR = A within round-off error.

for i = 1:numSamples
    Q = C_actual(:,:,i)';
    I = Q'*Q
    R = R_actual(:,:,i);
    isequal(R,triu(R))
    relative_error = norm(double(Q*R - A(:,:,i)))/norm(double(A(:,:,i)))
end

I = 
    1.0000    0.0000   -0.0000
    0.0000    1.0000   -0.0000
   -0.0000   -0.0000    1.0000

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 46
        FractionLength: 36

ans = logical
   1

relative_error = 1.3990e-05

I = 
    1.0000    0.0000   -0.0000
    0.0000    1.0000   -0.0000
   -0.0000   -0.0000    1.0000

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 46
        FractionLength: 36

ans = logical
   1

relative_error = 2.4302e-05

I = 
    1.0000    0.0000   -0.0000
    0.0000    1.0000    0.0000
   -0.0000    0.0000    1.0000

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 46
        FractionLength: 36

ans = logical
   1

relative_error = 2.9015e-05

Verify block latency

The latency of the Systolic QR Decomposition block depends on the datatype, dimension, and complexity of input matrices A and B.

Use the embblk.latency.systolicQRBlockTiming function to calculate the expected latency and throughput.

[expThroughput,expLatency] = embblk.latency.systolicQRBlockTiming(tv.A,tv.B)

expThroughput = 25

expLatency = 72

Retrieve actual block throughput and latency from the simulation data.

tDataIn = find(out.logsout.get('Input Handshake').Values.Data == 1);
tDataOut = find(out.logsout.get('Output Handshake').Values.Data == 1);
actualthroughput = diff(tDataIn)

actualthroughput = 4×1

    25
    25
    25
    25

actualLatency = tDataOut - tDataIn(1:numSamples)

actualLatency = 3×1

    72
    72
    72

Ports

Input

A — Matrix A

matrix

Matrix A, specified as a matrix. A is an m-by-n matrix where m ≥ 2 and n ≥ 2. If B is single or double, A must be the same data type as B. If A is a fixed-point data type, A must be signed, use binary-point scaling, and have the same word length as B. Slope-bias representation is not supported for fixed-point data types.

Dependencies

Use the Signal type parameter to specify the complexity of the input data.

Data Types: single | double | fixed point
Complex Number Support: Yes

B — Matrix B

matrix

Matrix B, specified as a matrix. B is an m-by-p matrix where m ≥ 2. If A is single or double, B must be the same data type as A. If B is a fixed-point data type, B must be signed, use binary-point scaling, and have the same word length as A. Slope-bias representation is not supported for fixed-point data types.

Dependencies

Use the Signal type parameter to specify the complexity of the input data.

Data Types: single | double | fixed point
Complex Number Support: Yes

validIn — Whether inputs are valid

scalar

Whether inputs are valid, specified as a Boolean scalar. This control signal indicates when the data from the A and B input ports are valid. When this value is 1 (true) and the value at readyIn is 1 (true), the block captures the values on the A and B input ports. When this value is 0 (false), the block ignores the input samples.

Tips

After sending a true validIn signal, there may be some delay before readyIn is set to false. To ensure all data is processed, you must wait until readyIn is set to false before sending another true validIn signal.

Data Types: Boolean

readyIn — Whether downstream block is ready

scalar

Whether downstream block is ready, specified as a Boolean scalar. This control signal monitors the ready port of the downstream block. When the readyIn value is 1 (true), and the value at validOut is 1 (true), the block outputs data to the downstream block. When the readyIn value is 0 (false), the downstream block is not ready to accept data. The Systolic QR Decomposition block pauses on the output stage and the ready signal remains 0 (false) until the readyIn signal is high.

Data Types: Boolean

restart — Whether to clear internal states

scalar

Whether to clear internal states, specified as a Boolean scalar. When this value is 1 (true), the block stops the current calculation and clears all internal states. When this value is 0 (false) and the validIn value is 1 (true), the block begins a new subframe.

Data Types: Boolean

Output

R — Matrix R

matrix

Economy size QR decomposition matrix R, returned as a matrix. R is an upper triangular matrix. The size of matrix R is n-by-n. R has the same data type as A.

Data Types: single | double | fixed point
Complex Number Support: Yes

C — Matrix C = Q'B

matrix

Economy size QR decomposition matrix C=Q'B, returned as a matrix. C has the same number of rows as R. C has the same data type as B.

Data Types: single | double | fixed point
Complex Number Support: Yes

validOut — Whether output data is valid

scalar

Whether output data is valid, returned as a Boolean scalar. This control signal indicates when the data at output ports R and C is valid. When this value is 1 (true), the block has successfully computed the R and C matrices. When this value is 0 (false), the output data is not valid.

Data Types: Boolean

ready — Whether block is ready

scalar

Whether block is ready, returned as a Boolean scalar. This control signal that indicates when the block is ready for new input data. When this value is 1 (true) and the validIn value is 1 (true), the block accepts input data in the next time step. When this value is 0 (false), the block ignores input data in the next time step.

Tips

After sending a true validIn signal, there may be some delay before ready is set to false. To ensure all data is processed, you must wait until ready is set to false before sending another true validIn signal.

Data Types: Boolean

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Number of rows in matrices A and B — Number of rows in matrices A and B

2 (default) | positive integer-valued scalar

Number of rows in input matrices A and B, specified as a positive integer-valued scalar.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	m
Values:	2 (default) | positive integer-valued scalar
Data Types:	char

Number of columns in matrix A — Number of columns in matrix A

2 (default) | positive integer-valued scalar

Number of columns in matrix A, specified as a positive integer-valued scalar.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	n
Values:	2 (default) | positive integer-valued scalar
Data Types:	char

Number of columns in matrix B — Number of columns in matrix B

1 (default) | positive integer-valued scalar

Number of columns in matrix B, specified as a positive integer-valued scalar.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	p
Values:	1 (default) | positive integer-valued scalar
Data Types:	char

Signal type — Complexity of matrices A and B

real (default) | complex

Complexity of matrices A and B, specified as real or complex.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	complexity
Values:	real (default) | complex
Data Types:	char

Algorithms

Choosing the Implementation Method

Systolic implementations prioritize speed of computations over space constraints, while burst implementations prioritize space constraints at the expense of speed of the operations. The following table illustrates the tradeoffs between the implementations available for matrix decompositions and solving systems of linear equations.

Implementation	Throughput	Latency	Area
Systolic	C	O(n)	O(mn2)
Partial-Systolic	C	O(m)	O(n2)
Partial-Systolic with Forgetting Factor	C	O(n)	O(n2)
Burst	O(n)	O(mn)	O(n)

Where C is a constant proportional to the word length of the data, m is the number of rows in matrix A, and n is the number of columns in matrix A.

For additional considerations in selecting a block for your application, see Choose a Block for HDL-Optimized Fixed-Point Matrix Operations.

AMBA AXI Handshake Process

This block uses the AMBA AXI handshake protocol [1]. The valid/ready handshake process is used to transfer data and control information. This two-way control mechanism allows both the manager and subordinate to control the rate at which information moves between manager and subordinate. A valid signal indicates when data is available. The ready signal indicates that the block can accept the data. Transfer of data occurs only when both the valid and ready signals are high.

Block Timing

The Systolic QR Decomposition block accepts and process A and B as full matrices. After computation, the block outputs the R and C matrices. The systolic implementation uses a pipelined structure, so the block can accept new matrix inputs before outputting the result of the current matrix.

For example, assume that the input A and B matrices are 3-by-3. Additionally assume that validIn asserts before ready, meaning that the upstream data source is faster than the QR decomposition.

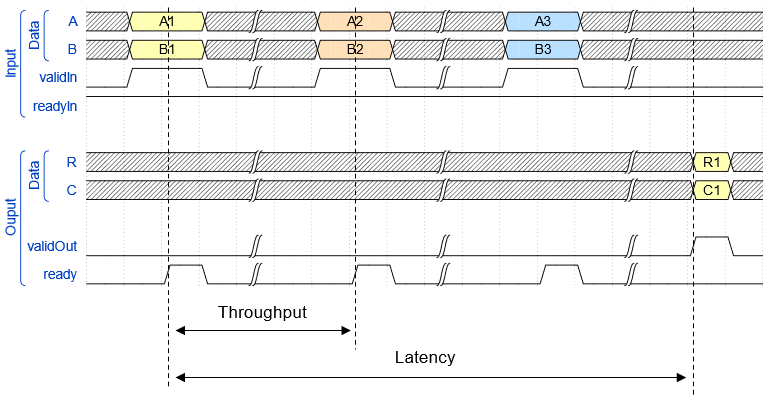
In the figure,

• A1 is the first A matrix, B1 is the first B matrix, and so on.

• Throughput — From a successful matrix input to the block being ready to accept the next matrix.

• Latency — From a successful matrix input to the block starting to output the corresponding solution.

The latency of the Systolic QR Decomposition block depends on the size (m, n, p), complexity, and word length (wl) of matrices A and B.

• If the data types of A and B are double, then wl is 53.

• If the data type of A and B are single, then wl is 24.

• If the data types of A and B are fixed point, then wl is the word length.

Use the embblk.latency.systolicQRBlockTiming function to calculate the latency and throughput.

[throughput,latency] = embblk.latency.systolicQRBlockTiming(A,B)

Hardware Resource Utilization

This block supports HDL code generation using the Simulink HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder) and Implement Digital Downconverter for FPGA (DSP HDL Toolbox).

This example data was generated by synthesizing the block on a Xilinx^® Zynq^®-7000 xc7z045 SoC. The synthesis tool was Vivado^® v2023.1 (win64).

Signal Type: Real

The following parameters were used for synthesis.

• Block parameters:

  • m = 4

  • n = 4

  • p = 1

  • Signal type: real

• Input matrix A and B type: sfix16_En10

• Target frequency: 200 MHz

Resource	Usage	Available	Utilization (%)
Slice LUTs	8451	218600	3.87
Slice Registers	1883	437200	0.43
DSPs	0	900	0.00
Block RAM Tile	0	545	0.00
URAM	0	0	0.00

	Value
Requirement	5 ns (200 MHz)
Data Path Delay	3.237 ns
Slack	1.744 ns
Clock Frequency	307.13 MHz

Signal Type: Complex

The following parameters were used for synthesis.

• Block parameters:

  • m = 4

  • n = 4

  • p = 1

  • Signal type: complex

• Input matrix A and B type: sfix16_En10

• Target frequency: 200 MHz

Resource	Usage	Available	Utilization (%)
Slice LUTs	29655	218600	13.57
Slice Registers	7048	437200	1.61
DSPs	0	900	0.00
Block RAM Tile	0	545	0.00
URAM	0	0	0.00

	Value
Requirement	5 ns (200 MHz)
Data Path Delay	3.244 ns
Slack	1.737 ns
Clock Frequency	306.47 MHz

References

[1] "AMBA AXI and ACE Protocol Specification Version E." https://developer.arm.com/documentation/ihi0022/e/AMBA-AXI3-and-AXI4-Protocol-Specification/Single-Interface-Requirements/Basic-read-and-write-transactions/Handshake-process

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

Slope-bias representation is not supported for fixed-point data types.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

General
ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Restrictions

Supports fixed-point data types only. Fixed-point data types must use signed binary-point scaling. Slope and bias scaled types are not supported.

Version History

Introduced in R2024a