Stratified Sampling
This example specifies a noise function to stratify the terminal value of a univariate equity price series. Simulation methods allow you to specify a noise process directly, as a callable function of time and state:
![]()
Stratified sampling is a variance reduction technique that constrains a proportion of sample paths to specific subsets (or strata) of the sample space.
This example specifies a noise function to stratify the terminal value of a univariate equity price series. Starting from known initial conditions, the function first stratifies the terminal value of a standard Brownian motion, and then samples the process from beginning to end by drawing conditional Gaussian samples using a Brownian bridge.
The stratification process assumes that each path is associated with a single stratified terminal value such that the number of paths is equal to the number of strata. This technique is called proportional sampling. This example is similar to, yet more sophisticated than, the one discussed in Simulating Interest Rates. Since stratified sampling requires knowledge of the future, it also requires more sophisticated time synchronization; specifically, the function in this example requires knowledge of the entire sequence of sample times.
The function implements proportional sampling by partitioning the unit interval into bins of equal probability by first drawing a random number uniformly distributed in each bin. The inverse cumulative distribution function of a standard N(0,1) Gaussian distribution then transforms these stratified uniform draws. Finally, the resulting stratified Gaussian draws are scaled by the square root of the terminal time to stratify the terminal value of the Brownian motion.
The noise function does not return the actual Brownian paths, but rather the Gaussian draws that drive it.
This example first stratifies the terminal value of a univariate, zero-drift, unit-variance-rate Brownian motion (bm) model:
![]()
Assume that 10 paths of the process are simulated daily over a three-month period. Also assume that each calendar month and year consist of 21 and 252 trading days, respectively.
rng(10203,'twister') dt = 1 / 252; % 1 day = 1/252 years nPeriods = 63; % 3 months = 63 trading days T = nPeriods * dt; % 3 months = 0.25 years nPaths = 10; % # of simulated paths obj = bm(0, 1, 'StartState', 0); sampleTimes = cumsum([obj.StartTime; ... dt(ones(nPeriods,1))]); z = Example_StratifiedRNG(nPaths, sampleTimes);
Simulate the standard Brownian paths by explicitly passing the stratified sampling function to the simulation (simulate) method.
X = obj.simulate(nPeriods, 'DeltaTime', dt, ... 'nTrials', nPaths, 'Z', z);
For convenience, reorder the output sample paths by reordering the three-dimensional output to a two-dimensional equivalent array.
X = squeeze(X);
Verify the stratification by recreating the uniform draws with proportional sampling.
rng(10203,'twister')
U = ((1:nPaths)' - 1 + rand(nPaths,1))/nPaths;Verify the stratification by transforming it to obtain the terminal values of standard Brownian motion.
WT = norminv(U) * sqrt(T); % Stratified Brownian motion.Verify the stratification by plotting the terminal values and output paths on the same figure.
plot(sampleTimes, X), hold('on') xlabel('Time (Years)'), ylabel('Brownian State') title('Terminal Stratification: Standard Brownian Motion') plot(T, WT, '. black', T, WT, 'o black') hold('off')
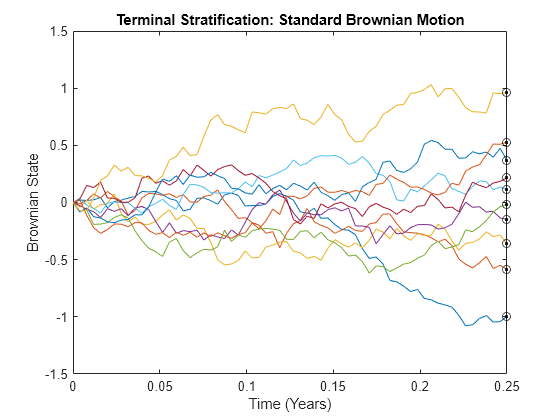
The last value of each sample path (the last row of the output array (X) coincides with the corresponding element of the stratified terminal value of the Brownian motion. This occurs because the simulated model and the noise generation function both represent the same standard Brownian motion.
However, you can use the same stratified sampling function to stratify the terminal price of constant-parameter geometric Brownian motion models. In fact, you can use the stratified sampling function to stratify the terminal value of any constant-parameter model driven by Brownian motion if the model's terminal value is a monotonic transformation of the terminal value of the Brownian motion.
To illustrate this, load the data set and simulate risk-neutral sample paths of the FTSE 100 index using a geometric Brownian motion (GBM) model with constant parameters:
![]()
where the average Euribor yield represents the risk-free rate of return.
Assume that the relevant information derived from the daily data is annualized, and that each calendar year comprises 252 trading days.
load Data_GlobalIdx2
returns = tick2ret(Dataset.FTSE);
sigma = std(returns) * sqrt(252);
rate = Dataset.EB3M;
rate = mean(360 * log(1 + rate));Create the GBM model using gbm, assuming the FTSE 100 starts at 100.
obj = gbm(rate, sigma, 'StartState', 100);Determine the sample time and simulate the price paths. In the following code, NSteps specifies the number of intermediate time steps within each time increment DeltaTime. Each increment DeltaTime is partitioned into NSteps subintervals of length DeltaTime/NSteps each, refining the simulation by evaluating the simulated state vector at NSteps–1 intermediate points. This refinement improves accuracy by allowing the simulation to more closely approximate the underlying continuous-time process without storing the intermediate information.
nSteps = 1; sampleTimes = cumsum([obj.StartTime ; ... dt(ones(nPeriods * nSteps,1))/nSteps]); z = Example_StratifiedRNG(nPaths, sampleTimes); rng(10203,'twister') [Y, Times] = obj.simBySolution(nPeriods, 'nTrials', nPaths,... 'DeltaTime', dt, 'nSteps', nSteps, 'Z', z); Y = squeeze(Y); % Reorder to a 2-D array plot(Times, Y) xlabel('Time (Years)'), ylabel('Index Level') title('FTSE 100 Terminal Stratification:Geometric Brownian Motion')
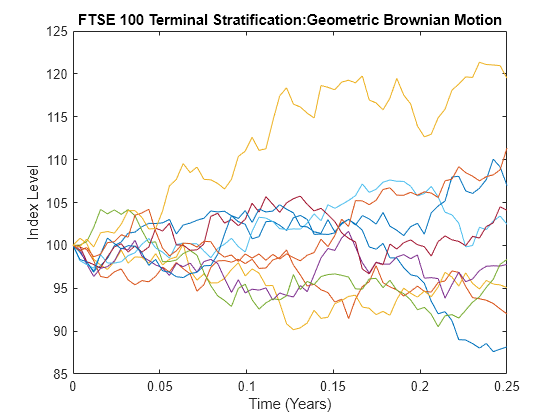
Although the terminal value of the Brownian motion shown in the latter plot is normally distributed, and the terminal price in the previous plot is lognormally distributed, the corresponding paths of each graph are similar. For another example of variance reduction techniques, see Simulate Interest Rates Through Interpolation.
See Also
sde | bm | gbm | merton | bates | drift | diffusion | sdeddo | sdeld | cev | cir | heston | hwv | sdemrd | rvm | roughbergomi | roughheston | ts2func | simulate | simByEuler | simBySolution | simByQuadExp | simBySolution | interpolate
Topics
- Simulating Equity Prices
- Simulating Interest Rates
- Price American Basket Options Using Standard Monte Carlo and Quasi-Monte Carlo Simulation
- Improving Performance of Monte Carlo Simulation with Parallel Computing
- Base SDE Models
- Drift and Diffusion Models
- Linear Drift Models
- Parametric Models
- SDEs
- SDE Models
- SDE Class Hierarchy
- Performance Considerations