Spectrum Estimator
Estimate power spectrum or power-density spectrum
Libraries:
DSP System Toolbox /
Estimation /
Power Spectrum Estimation
Description
The Spectrum Estimator block outputs the power spectrum or power-density spectrum of a real or complex input signal, using the Welch method of averaged modified periodograms and the filter bank approach.
When you choose the filter bank approach, the block uses an analysis filter bank to estimate the power spectrum. The filter bank approach produces a spectral estimate with a higher resolution, a more accurate noise floor, and more precise peaks than the Welch method, with low or no spectral leakage. They come at the expense of increased computation and slower tracking.
When you choose the Welch method, the block computes the averaged modified periodograms to compute the spectral estimate. The block buffers the input data into overlapping segments. Use the block parameters to set the length of the data segments, the amount of data overlap between consecutive segments, and other features of the power spectrum.
For more information on the Welch method and the filter bank method, see Algorithms.
Examples
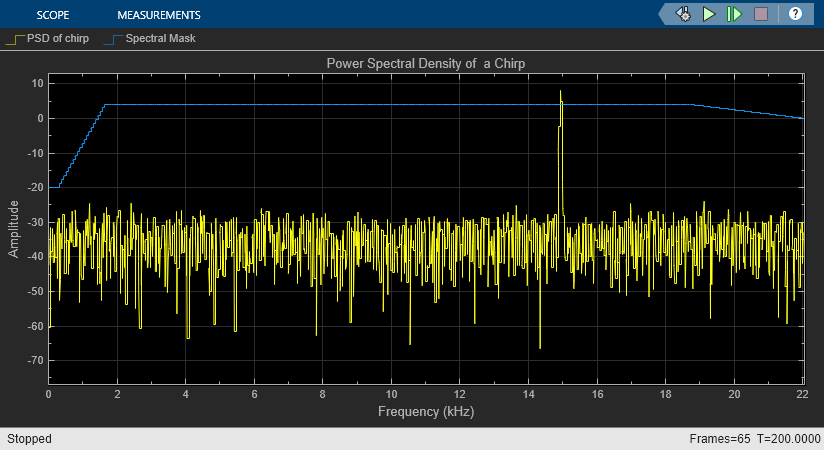
Estimate Power Spectral Density of Chirp
Estimate power spectral density of chirp and compare with Bluetooth spectral mask.
Ports
Input
Specify the input signal as a vector or matrix. The block treats each column of the input as a separate channel. If the input is a two-dimensional signal, the first dimension represents the channel length (or frame size) and the second dimension represents the number of channels. If the input is a one-dimensional signal, then it is interpreted as a single channel.
Data Types: single | double
Complex Number Support: Yes
Output
Power spectrum or power-density spectrum that the block estimates, returned as a vector or a matrix.
Data Types: single | double
Max-hold spectrum, returned as a vector or a matrix. The block computes the max-hold spectrum by keeping, at each frequency bin, the maximum value of all the power spectrum estimates.
Data Types: single | double
Min-hold spectrum, returned as a vector or a matrix. The block computes the min-hold spectrum by keeping, at each frequency bin, the minimum value of all the power spectrum estimates.
Data Types: single | double
Output frequencies, returned as a column vector.
Data Types: single | double
Effective resolution bandwidth, returned as a scalar.
Data Types: single | double
Parameters
Main Tab
Specify the spectral estimation method as one of these options.
Filter bank— Analysis filter bank splits the broadband input signal into multiple narrow subbands. The block computes the power in each narrow frequency band, and the computed value is the spectral estimate over the respective frequency band.Welch— The block uses the Welch averaged modified periodograms method to compute the power spectrum over the narrow subbands.
Specify the number of filter coefficients, or taps, for each frequency band as a positive integer. This value corresponds to the number of filter coefficients per polyphase branch. The total number of filter coefficients is equal to Number of taps per band times the FFT length.
Dependencies
To enable this parameter, set Method to
Filter bank.
Specify the type of spectrum to compute one of these:
Power— Compute the power spectrum.Power density— Compute the power spectral density.
Specify the frequency resolution method as one of these options.
Auto— The Spectrum Estimator block computes the resolution bandwidth (RBW) so that the frequency span fits 1024 RBW intervals.Welch method — The window length, winLen, is calculated using . NENBW is the equivalent noise bandwidth of the window and Fs is the sample rate.
Filter bank method — The FFT length is the ceiling of the ratio of Sample rate (Hz) to the computed resolution bandwidth.
RBW— Specify the resolution bandwidth, which is used to determine the window length (Welch method) or the FFT length (filter bank method). When the block uses the Welch method, the behavior is equivalent to that of the Spectrum Analyzer block. The window length is calculated using . NENBW is the equivalent noise bandwidth of the window and Fs is the sample rate. The FFT length is equal to the ceiling of the ratio of Sample rate (Hz) to RBW (Hz).Window length— Specify the window or segment length to use in the Welch algorithm. This option is available when you set Method toWelch.Number of frequency bands— Specify the number of polyphase branches of the analysis filter bank. This value corresponds to the FFT length that the filter bank uses. To enable this option, set Method toFilter bank.
Specify the resolution bandwidth as a positive scalar in Hz. The
ceiling of the ratio of the frequency span to RBW must be greater than
2.
Dependencies
To enable this parameter, set Frequency resolution
method to RBW.
Specify the source of the window length value as one of these:
Same as input frame length— Window length is equal to the frame size of the input. Specify this option to obtain behavior equivalent to that of the Periodogram block.Specify on dialog— Window length is the value you specify in the Window length parameter.
Dependencies
To enable this parameter, set
Method to
Welch.Frequency resolution method to
Window length.
Specify the length of the window used to compute the spectrum estimate
as a positive integer scalar greater than 2.
Dependencies
To enable this parameter, set
Method to
Welch.Frequency resolution method to
Window length.Window length source to
Specify on dialog.
Specify the source of the number of frequency bands as one of these:
Same as input frame length— The FFT length is equal to the frame size of the input.Specify on dialog— The FFT length is the value you specify in Number of bands.
Dependencies
To enable this parameter, set
Method to
Filter bank.Frequency resolution method to
Number of frequency bands.
Specify the number of frequency bands or the FFT length the filter bank uses to compute the power spectral estimate as a positive scalar.
Dependencies
To enable this parameter, set
Method to
Filter bank.Frequency resolution method to
Number of frequency bands.Number of bands source to
Specify on dialog.
Specify the source of the FFT length value as one of these:
Auto— The block sets the FFT length to the frame size of the input.Property— The block sets the FFT length to the value you specify in FFT length.
Dependencies
To enable this parameter, set
Method to
Welch.Frequency resolution method to
Window length.
Specify the FFT length as a positive integer. The block uses this to compute the spectrum estimates.
Dependencies
To enable this parameter, set
Method to
Welch.Frequency resolution method to
Window length.FFT length source to
Property.
When you select this check box, the block algorithm computes the block sample rate as N/Ts, where N is the frame size of the input signal and Ts is the sample time of the input signal. By default, the block inherits its sample rate from the input signal. When you clear this check box, the block sample rate is the value you specify in Sample rate (Hz).
Dependencies
To enable this parameter, do one of the following:
Set Method to
Welchand Frequency resolution method toWindow length.Set Method to
Filter bankand Frequency resolution method toNumber of frequency bands.
Specify the sample rate of the input signal as a positive scalar.
Dependencies
To enable this parameter, do one of the following:
Set Frequency resolution method to
AutoorRBW.Set Method to
Welch, Frequency resolution method toWindow length, and clear the Inherit sample rate from input check box.Set Method to
Filter bank, Frequency resolution method toNumber of frequency bands, and clear the Inherit sample rate from input check box.
Specify the window function used by the Welch algorithm as
Chebyshev, Flat
Top, Hamming,
Hann, Kaiser,
or Rectangular. The default value is
Hann.
Dependencies
To enable this parameter, set Method to
Welch.
Specify the sidelobe attenuation of the window in dB as a positive scalar greater than
or equal to 45.
Dependencies
To enable this parameter, set Method to
Welch and Window
function to Chebyshev or
Kaiser.
Specify the averaging method as Exponential
(default) or Running. In the exponential
method, the block computes the average over samples weighted by an
exponentially decaying forgetting factor. In the running averaging
method, the block computes an equally weighted average of specified
number of spectrum estimates defined by Number of spectral
averages parameter.
Specify the number of spectral averages as a positive integer. The spectrum estimator computes the current power spectrum estimate by averaging the last N power spectrum estimates, where N is the number of spectral averages defined in Number of spectral averages.
Dependencies
To enable this parameter, set Averaging
method to Running.
Select this check box to specify the forgetting factor from an input port. When you do not select this check box, you must specify the forgetting factor through the Forgetting factor parameter.
Dependencies
To enable this parameter, set Averaging
method to
Exponential.
Specify the exponential weighting forgetting factor as a scalar value greater than 0 and smaller than or equal to 1.
Dependencies
To enable this parameter, set Averaging
method to Exponential and
clear the Specify forgetting factor from input
port parameter.
Advanced Tab
Specify the percentage of overlap between successive data windows as a
scalar from 0 and 100.
Dependencies
To enable this parameter, on the Main Tab,
set Method to
Welch.
Specify the load used as a reference to compute the power values as a real positive scalar expressed in ohms.
Specify the frequency range of the spectrum estimator as one of these:
Centered— The spectrum estimator computes the centered two-sided spectrum of a complex or real input signal. The length of the spectrum estimate is equal to the FFT length. The spectrum estimate is computed over the frequency range (-SampleRate/2 SampleRate/2] when the FFT length is even and(-SampleRate/2 SampleRate/2)when the FFT length is odd.One-sided— The spectrum estimator computes the one-sided spectrum of a real input signal. When the FFT length,NFFT, is even, the spectrum estimate has length (NFFT/2) +1and is computed over the frequency range[0 SampleRate/2].SampleRateis the sample rate of the input signal. WhenNFFTis odd, the spectrum estimate has length (NFFT+ 1)/2and is computed over the frequency range [0 SampleRate/2).Two-sided— The spectrum estimator computes the two-sided spectrum of a complex or real input signal. The length of the spectrum estimate is equal to the FFT length. The spectrum estimate is computed over the frequency range [0 SampleRate), whereSampleRateis the sample rate of the input signal.
Specify the units used to measure power as one of these:
dBm— The spectrum estimator measures power in decibel-milliwatts.Watts— The spectrum estimator measures power in watts.dBW— The spectrum estimator measures power in decibel-watts.
When you select this check box, the block outputs the max-hold spectrum of the input signal through the P_max port. The block computes the max-hold spectrum by keeping, at each frequency bin, the maximum value of all the power spectrum estimates. By default, this check box is not selected.
When you select this check box, the block outputs the min-hold spectrum of the input signal through the P_min port. The block computes the min-hold spectrum by keeping, at each frequency bin, the minimum value of all the power spectrum estimates. By default, this check box is not selected.
When you select this check box, the block outputs the frequency vector through the F port. By default, this check box is not selected.
When you select this check box, the block computes and outputs the effective resolution bandwidth through the RBW port. By default, this check box is not selected.
Specify the type of simulation to run as one of these:
Interpreted execution— Simulate model using the MATLAB® interpreter. This option shortens startup time.Code generation— Simulate model using generated C code. The first time you run a simulation, Simulink® generates C code for the block. The C code is reused for subsequent simulations, as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
When you choose the Welch method, the power spectrum estimate is averaged modified periodograms.
Given the signal input x:
Multiply
xby the window and scale the result by the window power.Compute the FFT of the signal
Yand take the square magnitude usingZ = Y.*conj(Y).Compute the current power spectrum estimate by taking the moving average of the last N number of Zs, and scaling the answer by the sample rate. For more information on the moving average methods, see Averaging Method.
When you select the filter bank method, the spectrum estimator uses an analysis filter bank to estimate the power spectrum. The filter bank splits a broadband input signal, x(n), of sample rate fs into multiple narrow band signals, y0(m), y1(m), … , yM-1(m), of sample rate fs/M.
The variable M represents the number of frequency bands in the
filter bank. When you specify FFT length, M equals the FFT length.
When you do not specify FFT length, M is equal to the number of rows
in the input signal. The number of taps per frequency band sets the number of filter
coefficients for each frequency band of the filter bank. The total number of filter
coefficients is equal to the number of taps per band multiplied by the number of
frequency bands M. For more information on the analysis filter bank
and how it is implemented, see the More About and the Algorithm sections in
dsp.Channelizer.
After the broadband input signal is split into multiple narrow bands, the spectrum estimator computes the power in each narrow band using the following equation. Each Zi value becomes the estimate of the power over that narrow frequency band.
where L is the length of the narrow band signal yi(m) and i = 1, 2, …, M−1.
The power values in all the narrow bands (denoted by Zi) form the Z vector.
The filter bank estimator algorithm averages the current Z vector with the previous Z vectors using one of the two moving average methods: running or exponential weighting. The output of the averaging operation forms the spectral estimate vector. For more information on the two averaging methods, see Averaging Method.

The algorithm calculates the moving average using one of these methods:
Running— For each frame of input, average the last N-scaled Z vectors, which are computed by the algorithm. The variable N is the value you specify for the number of spectral averages. If the algorithm does not have enough Z vectors, the algorithm uses zeros to fill the empty elements.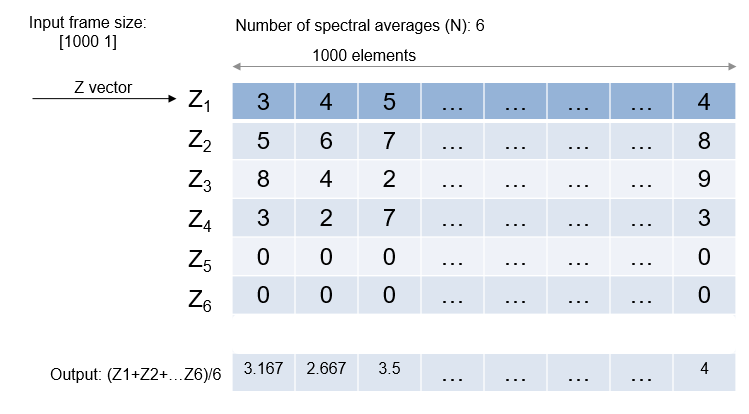
Exponential— The moving average algorithm using the exponential weighting method updates the weights and computes the moving average recursively for each Z vector that comes in by using the following recursive equations:λ — Forgetting factor
— Weighting factor applied to the current Z vector
— Current Z vector
— Moving average until the previous Z vector
— Effect of the previous Z vectors on the average
— Moving average including the current Z vector
References
[1] Hayes, Monson H. Statistical Digital Signal Processing and Modeling. Hoboken, NJ: John Wiley & Sons, 1996.
[2] Kay, Steven M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice Hall, 1999.
[3] Stoica, Petre, and Randolph L. Moses. Spectral Analysis of Signals. Englewood Cliffs, NJ: Prentice Hall, 2005.
[4] Welch, P. D. “The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms.” IEEE Transactions on Audio and Electroacoustics. Vol. 15, No. 2, June 1967, pp. 70–73.
[5] Bluetooth Specification Version 4.2. Bluetooth SIG. December 2014, p. 217. Specification of the Bluetooth System
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2015b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)