iirlp2mbc

Transform IIR lowpass filter to IIR complex multiband filter

Syntax

[num,den,allpassNum,allpassDen] = iirlp2mbc(b,a,wo,wt)

Description

[num,den,allpassNum,allpassDen] = iirlp2mbc(b,a,wo,wt) transform an IIR lowpass filter to an IIR complex multiband filter.

The iirlp2mbc returns the numerator and denominator coefficients of the transformed complex IIR multiband filter. The function also returns the numerator, allpassNum, and the denominator, allpassDen, of the M^th order allpass mapping filter. The prototype lowpass filter is specified with the numerator b and the denominator a.

The function transforms a real lowpass prototype filter to a multiband filter by applying an M^th-order real lowpass to complex multiple bandpass frequency mapping. Parameter M is the number of times an original feature is replicated in the transformed filter. For more details, see IIR Lowpass Filter to IIR Complex Multiband Filter Transformation.

Examples

Transform Lowpass Filter to Complex Multiband Filter

Transform a real lowpass IIR filter to a complex multiband IIR filter using the iirlp2mbc function.

Input Lowpass IIR Filter

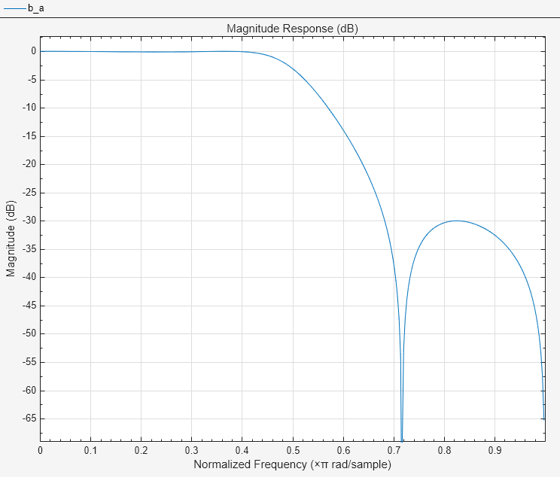
Design a prototype real IIR lowpass elliptic filter with a gain of about –3 dB at 0.5π rad/sample.

[b,a] = ellip(3,0.1,30,0.409);
filterAnalyzer(b,a)

Transform Filter Using iirlp2mbc

Transform the real prototype lowpass filter into a complex multiband filter with two passbands.

Specify the prototype filter as a vector of numerator and denominator coefficients, b and a respectively.

[num,den] = iirlp2mbc(b,a,0.5,[-7 -5 6 8]/10);

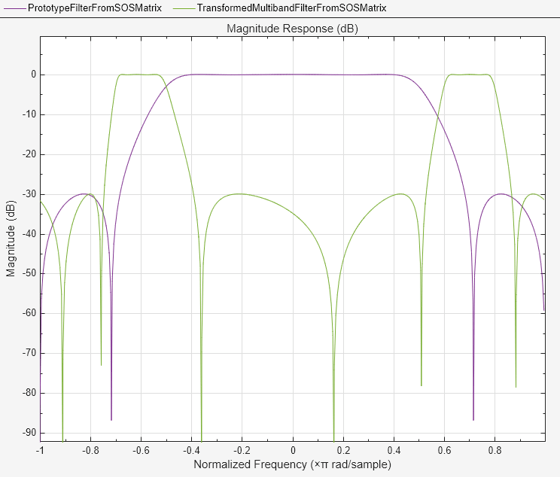
Compare the magnitude response of the filters. iirlp2mbc replicates the desired feature at 0.5 in the lowpass filter at four locations in the multiband filter.

filterAnalyzer(b,a,num,den,FrequencyRange="centered",...
    FilterNames=["PrototypeFilter_TFForm",...
    "TransformedMultibandFilter"])

Alternatively, you can also specify the input lowpass IIR filter as a matrix of coefficients. Pass the second-order section matrices as inputs. The transformed filter is a fourth-order section filter given by the numerator and the denominator coefficients num2 and den2.

ss = tf2sos(b,a);
[num2,den2] = iirlp2mbc(ss(:,1:3),ss(:,4:6),0.5,[-7 -5 6 8]/10);

To visualize the magnitude response of the fourth-order section filter, first pass the filter coefficients to the dsp.FourthOrderSectionFilter object. Then, use this object as an input to the filter analyzer.

fos = dsp.FourthOrderSectionFilter(Numerator=num2,...
    Denominator=den2);

Use the sos2ctf function to convert the second-order section matrices to the cascaded transfer function form.

[b_ctf,a_ctf] = sos2ctf(ss);

Compare the magnitude response of the filters.

filterAnalyzer(b_ctf,a_ctf,fos,FrequencyRange="centered",...
    FilterNames=["PrototypeFilterFromSOSMatrix",...
    "TransformedMultibandFilterFromSOSMatrix"]);

Copyright 2012–2024 The MathWorks, Inc.

Input Arguments

b — Numerator coefficients of prototype lowpass IIR filter

row vector | matrix

Numerator coefficients of the prototype lowpass IIR filter, specified as either:

• Row vector –– Specifies the values of [b₀, b₁, …, b_n], given this transfer function form:

  $$H(z)=\frac{B(z)}{A(z)}=\frac{b_0+b_1{z}^{-1}+\cdots +b_n{z}^{-n}}{a_0+a_1{z}^{-1}+\cdots +a_n{z}^{-n}},$$

  where n is the order of the filter.

• Matrix –– Specifies the numerator coefficients in the form of an P-by-(Q+1) matrix, where P is the number of filter sections and Q is the order of each filter section. If Q = 2, the filter is a second-order section filter. For higher-order sections, make Q > 2.

  $$b=\left[\begin{array}{ccccc}{b}_{01}& b_{11}& b_{21}& \mathrm{...}& b_{Q1}\\ b_{02}& b_{12}& b_{22}& \mathrm{...}& b_{Q2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ b_{0P}& b_{1P}& b_{2P}& \cdots & b_{QP}\end{array}\right]$$

  In the transfer function form, the numerator coefficient matrix b_ik of the IIR filter can be represented using the following equation:

  $$H(z)={\displaystyle \prod _{k=1}^P{H}_k}(z)={\displaystyle \prod _{k=1}^P\frac{b_{0k}+b_{1k}{z}^{-1}+b_{2k}{z}^{-2}+\cdots +b_{Qk}{z}^{-Q}}{a_{0k}+a_{1k}{z}^{-1}+a_{2k}{z}^{-2}+\cdots +a_{Qk}{z}^{-Q}}},$$

  where,

  • a –– Denominator coefficients matrix. For more information on how to specify this matrix, see a.

  • k –– Row index.

  • i –– Column index.

  When specified in the matrix form, b and a matrices must have the same number of rows (filter sections) Q.

Data Types: single | double
Complex Number Support: Yes

a — Denominator coefficients of prototype lowpass IIR filter

row vector | matrix

Denominator coefficients for a prototype lowpass IIR filter, specified as one of these options:

• Row vector –– Specifies the values of [a₀, a₁, …, a_n], given this transfer function form:

  $$H(z)=\frac{B(z)}{A(z)}=\frac{b_0+b_1{z}^{-1}+\cdots +b_n{z}^{-n}}{a_0+a_1{z}^{-1}+\cdots +a_n{z}^{-n}},$$

  where n is the order of the filter.

• Matrix –– Specifies the denominator coefficients in the form of an P-by-(Q+1) matrix, where P is the number of filter sections and Q is the order of each filter section. If Q = 2, the filter is a second-order section filter. For higher-order sections, make Q > 2.

  $$a=\left[\begin{array}{ccccc}{a}_{01}& a_{11}& a_{21}& \cdots & a_{Q1}\\ a_{02}& a_{12}& a_{22}& \cdots & a_{Q2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_{0P}& a_{1P}& a_{2P}& \cdots & a_{QP}\end{array}\right]$$

  In the transfer function form, the denominator coefficient matrix a_ik of the IIR filter can be represented using the following equation:

  $$H(z)={\displaystyle \prod _{k=1}^P{H}_k}(z)={\displaystyle \prod _{k=1}^P\frac{b_{0k}+b_{1k}{z}^{-1}+b_{2k}{z}^{-2}+\cdots +b_{Qk}{z}^{-Q}}{a_{0k}+a_{1k}{z}^{-1}+a_{2k}{z}^{-2}+\cdots +a_{Qk}{z}^{-Q}}},$$

  where,

  • b –– Numerator coefficients matrix. For more information on how to specify this matrix, see b.

  • k –– Row index.

  • i –– Column index.

  When specified in the matrix form, a and b matrices must have the same number of rows (filter sections) P.

Data Types: single | double
Complex Number Support: Yes

wo — Frequency value to transform from prototype filter

positive scalar

Frequency value to transform from the prototype filter, specified as a positive scalar. Frequency wo should be normalized to be between 0 and 1, with 1 corresponding to half the sample rate.

Data Types: single | double

wt — Desired frequency locations in transformed target filter

row vector

Desired frequency locations in the transformed target filter, specified as a row vector. Frequencies in wt should be normalized to be between -1 and 1, with 1 corresponding to half the sample rate. The value of M which is equal to the number of times an original feature is replicated in the transformed filter equals the length of the wt vector.

Data Types: single | double

Output Arguments

num — Numerator coefficients of transformed multiband filter

row vector | matrix

Numerator coefficients of the transformed multiband filter, returned as one of the following:

• Row vector of length Mn/2+1, where M is the number of times an original feature is replicated in the transformed filter and n is the order of the input filter. The value of M equals the length of the wt vector.

  The num output is a row vector when the input coefficients b and a are row vectors.

• P-by-(QM/2+1) matrix, where P is the number of filter sections, Q is the order of each section of the transformed filter, and M is the number of times an original feature is replicated in the transformed filter.

  The num output is a matrix when the input coefficients b and a are matrices.

Data Types: single | double
Complex Number Support: Yes

den — Denominator coefficients of transformed multiband filter

row vector | matrix

Denominator coefficients of the transformed multiband filter, returned as one of the following:

• Row vector of length Mn/2+1, where M is the number of times an original feature is replicated in the transformed filter and n is the order of the input filter. The value of M equals the length of the wt vector.

  The den output is a row vector when the input coefficients b and a are row vectors.

• P-by-(QM/2+1) matrix, where P is the number of filter sections, Q is the order of each section of the transformed filter, and M is the number of times an original feature is replicated in the transformed filter.

  The den output is a matrix when the input coefficients b and a are matrices.

Data Types: single | double
Complex Number Support: Yes

allpassNum — Numerator coefficients of mapping filter

row vector

Numerator coefficients of the mapping filter, returned as a row vector.

Data Types: single | double
Complex Number Support: Yes

allpassDen — Denominator coefficients of mapping filter

row vector

Denominator coefficients of the mapping filter, returned as a row vector.

Data Types: single | double
Complex Number Support: Yes

More About

IIR Lowpass Filter to IIR Complex Multiband Filter Transformation

IIR lowpass filter to IIR complex multiband filter transformation effectively places one feature of the original filter, located at frequency wo, at the required target frequency locations, wt1, … ,wtM.

Relative positions of other features of the original filter do not change in the target filter. This means that it is possible to select two features of an original filter, F₁ and F₂, with F₁ preceding F₂. Feature F₁ will still precede F₂ after the transformation. However, the distance between F₁ and F₂ will not be the same before and after the transformation.

Choice of the feature subject to this transformation is not restricted to the cutoff frequency of an original lowpass filter. You can choose to transform any feature of the original filter like stopband edge, DC, deep minimum in the stopband, or others.

The IIR lowpass filter to IIR complex multiband filter transformation can also be used for transforming other types of filters, for example, notch filters or resonators can be easily replicated at a number of required frequency locations. A good application would be an adaptive tone cancellation circuit reacting to the changing number and location of tones.

References

[1] Krukowski, A., and I. Kale. “High-Order Complex Frequency Transformations,” Internal report No. 27/2001. Applied DSP and VLSI Research Group, University of Westminster.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2011a