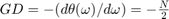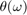dsp.Differentiator
Direct form FIR fullband differentiator filter
Description
The dsp.Differentiator
System object™ applies a fullband differentiator filter on the input signal to differentiate
all its frequency components. This object uses an FIR equiripple filter design to design the
differentiator filter. The ideal frequency response of the differentiator is for . You can design the filter with minimum order with a specified order. This
object supports fixed-point operations.
To filter each channel of your input:
Create the
dsp.Differentiatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
This object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.
Creation
Description
DF = dsp.DifferentiatorDF, which independently filters each channel of the
input over time using the given design specifications.
DF = dsp.Differentiator(Name=Value)FilterOrder to 15.
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1996.
Extended Capabilities
Version History
Introduced in R2016a
See Also
Functions
Objects
dsp.HighpassFilter|dsp.VariableBandwidthFIRFilter|dsp.VariableBandwidthIIRFilter|dsp.FIRFilter|dsp.SOSFilter