dsp.BiquadFilter
(To be removed) IIR filter using biquadratic structures
The dsp.BiquadFilter object will be removed in a future release. Use
the dsp.SOSFilter
object instead. For more information on updating your code, see Version History.
Description
The dsp.BiquadFilter object implements a cascade of biquadratic
sections, where the coefficients for each section are supplied by a separate row of an
N-by-6 second-order sections (SOS) matrix. Each row of the SOS
matrix contains the numerator and denominator coefficients of the corresponding section
of the filter. The resulting filter can be applied to a vector or matrix input, where
each column represents a channel of data that is processed independently.
To implement an IIR filter structure using biquadratic or SOS:
Create the
dsp.BiquadFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
biquad = dsp.BiquadFilterbiquad, which independently filters each
channel (column) of the input over time using the SOS section [1 0.3
0.4 1 0.1 0.2] with a direct-form II transposed structure.
biquad = dsp.BiquadFilter(sosmatrix,scalevalues) returns
a biquadratic filter object, with the SOSMatrix property
set to sosmatrix and the ScaleValues
property set to scalevalues.
biquad = dsp.BiquadFilter(
sets properties using one or more name-value arguments. For
example, to specify the filter structure of the biquadratic
filter as "Direct form II", set
Name=Value)Structure to "Direct Form
II".
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Specify the filter structure as "Direct form
I", "Direct form I
transposed", "Direct form
II", "Direct form II
transposed".
Specify the source of the SOS matrix as
"Property" or "Input
port".
Specify the second-order section (SOS) matrix as an N-by-6 matrix, where N is the number of sections in the filter. Each row of the SOS matrix contains the numerator and denominator coefficients of the corresponding section of the filter. The system function, H(z), of a biquad filter is:
The coefficients are ordered in the rows of the SOS
matrix as (b0,
b1,b2,1,
–a1,
–a2). You can use coefficients of real or complex values. This
property applies only when you set the SOSMatrixSource
property to Property. The leading denominator coefficient
of the biquad filter, a0, equals 1 for each filter section, regardless of the
specified value.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Specify the scale values to apply before and after each section of a
biquad filter. ScaleValues must be either
a scalar or a vector of length N+1, where
N is the number of sections. If you set this property
to a scalar, the scalar value is used as the gain value only before the
first filter section. The remaining gain values are set to
1. If you set this property to a vector of
N+1values, each value is used for a separate section
of the filter.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Specify the initial conditions of the filter states when the
Structure property is one of | Direct form
II | Direct form II transposed |. The
number of states or delay elements (zeros and poles) in a direct-form II
biquad filter equals twice the number of filter sections. You can specify
the initial conditions as a scalar, vector, or matrix.
When you specify a scalar value, the biquad filter initializes all delay elements in the filter to that value. When you specify a vector of length equal to the number of delay elements in the filter, each vector element specifies a unique initial condition for the corresponding delay element.
The biquad filter applies the same vector of initial conditions to each channel of the input signal. When you specify a vector of length equal to the product of the number of input channels and the number of delay elements in the filter, each element specifies a unique initial condition for the corresponding delay element in the corresponding channel. When you specify a matrix with the same number of rows as the number of delay elements in the filter, and one column for each channel of the input signal, each element specifies a unique initial condition for the corresponding delay element in the corresponding channel.
Dependencies
This property applies only when you set the
Structure property to one of Direct
form II or Direct form II
transposed.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Specify the initial conditions of the filter states on the side of the filter structure with the zeros. The number of states or delay elements in the numerator of a direct-form I biquad filter equals twice the number of filter sections. You can specify the initial conditions as a scalar, vector, or matrix. When you specify a scalar, the biquad filter initializes all delay elements on the zeros side in the filter to that value. When you specify a vector of length equal to the number of delay elements on the zeros side in the filter, each vector element specifies a unique initial condition for the corresponding delay element on the zeros side.
The biquad filter applies the same vector of initial conditions to each channel of the input signal. When you specify a vector of length equal to the product of the number of input channels and the number of delay elements on the zeros side in the filter, each element specifies a unique initial condition for the corresponding delay element on the zeros side in the corresponding channel. When you specify a matrix with the same number of rows as the number of delay elements on the zeros side in the filter, and one column for each channel of the input signal, each element specifies a unique initial condition for the corresponding delay element on the zeros side in the corresponding channel.
Dependencies
This property applies only when you set the
Structure property to one of Direct
form I or Direct form I
transposed.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Specify the initial conditions of the filter states on the side of the filter structure with the poles. The number of denominator states, or delay elements, in a direct-form I (noncanonic) biquad filter equals twice the number of filter sections. You can specify the initial conditions as a scalar, vector, or matrix. When you specify a scalar, the biquad filter initializes all delay elements on the poles side of the filter to that value. When you specify a vector of length equal to the number of delay elements on the poles side in the filter, each vector element specifies a unique initial condition for the corresponding delay element on the poles side.
The object applies the same vector of initial conditions to each channel of the input signal. When you specify a vector of length equal to the product of the number of input channels and the number of delay elements on the poles side in the filter, each element specifies a unique initial condition for the corresponding delay element on the poles side in the corresponding channel. When you specify a matrix with the same number of rows as the number of delay elements on the poles side in the filter, and one column for each channel of the input signal, each element specifies a unique initial condition for the corresponding delay element on the poles side in the corresponding channel.
Dependencies
This property only applies when you set the
Structure property to one of Direct
form I or Direct form I
transposed.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
When this Boolean property is set to true, the biquad
filter removes all unity scale gain computations. This reduces the number of
computations and increases the fixed-point accuracy.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property.
Select how to specify scale values. By default, this property is
true, and the scale values are specified via the
input port. When this property is false, all scale values
are 1.
Dependencies
This property applies only when the
SOSMatrixSource property is Input
port.
Fixed-Point Properties
Specify the rounding method.
Specify the overflow action as one of Wrap or
Saturate.
Specify the multiplicand fixed-point data type as one of Same
as output or Custom.
Dependencies
This property applies only when you set the
Structure property to Direct form
I transposed.
Specify the multiplicand fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of
Auto.
Dependencies
This property applies only when you set the
MultiplicandDataType property to
Custom.
Specify the section input fixed-point data type as either
Same as input or
Custom.
Specify the section input fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of
Auto.
Dependencies
This property applies only when you set the
SectionInputDataType property to
Custom.
Specify the section output fixed-point data type as either
Same as section input or
Custom.
Specify the section output fixed-point type as a signed, scaled
numerictype (Fixed-Point Designer) object
with a Signedness of
Auto.
Dependencies
This property applies only when you set the
SectionOutputDataType property to
Custom.
Specify the numerator coefficients fixed-point data type as
Same word length as input or
Custom. Setting this property also sets the
DenominatorCoefficientsDataType and
ScaleValuesDataType properties to the same
value.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property.
Specify the numerator coefficients fixed-point type as a numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
word length of the
CustomNumeratorCoefficientsDataType,
CustomDenominatorCoefficientsDataType, and
CustomScaleValuesDataType properties must be
the same.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property and the
NumeratorCoefficientsDataType property to
Custom.
Specify the denominator coefficients fixed-point data type as
Same word length as input or
Custom. Setting this property also sets the
NumeratorCoefficientsDataType and
ScaleValuesDataType properties to the same
value.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property.
Specify the denominator coefficients fixed-point type as a numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorCoefficientsDataType,
CustomDenominatorCoefficientsDataType, and
CustomScaleValuesDataType properties must have
the same word lengths.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property and the
DenominatorCoefficientsDataType property to
Custom.
Specify the scale values fixed-point data type as Same word
length as input or Custom. Setting this
property also sets the
NumeratorCoefficientsDataType and
DenominatorCoefficientsDataType properties to
the same value.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property.
Specify the scale values fixed-point type as a numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorCoefficientsDataType,
CustomDenominatorCoefficientsDataType, and
CustomScaleValuesDataType properties must have
the same word lengths.
Dependencies
This property applies only when you set the
SOSMatrixSource property to
Property and the
ScaleValuesDataType property to
Custom.
Specify the mode to determine the numerator product fixed-point data type as:
Same as input(default) — The numerator product word and fraction lengths are same as that of the input.Custom— Enables theCustomNumeratorProductDataTypeproperty, which you can use to specify the custom numerator product data type. Specify the data type as anumerictypeobject.Full precision— Use full-precision rules to specify the data type. These rules provide the most accurate fixed-point numerics. The rules prevent quantization from occurring within the object. Bits are added, as needed, so that no roundoff or overflow occurs. For more information, see Full Precision for Fixed-Point System Objects.
Setting this property also sets the
DenominatorProductDataType property to the same
value.
Specify the product fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorProductDataType and
CustomDenominatorProductDataType properties
must have the same word lengths.
Dependencies
This property applies only when you set the
NumeratorProductDataType property to
Custom.
Specify the mode to determine the denominator product fixed-point data type as:
Same as input(default) — The denominator product word and fraction lengths are same as that of the input.Custom— Enables theCustomDenominatorProductDataTypeproperty, which you can use to specify the custom denominator product data type. Specify the data type as anumerictypeobject.Full precision— Use full-precision rules to specify the data type. These rules provide the most accurate fixed-point numerics. The rules prevent quantization from occurring within the object. Bits are added, as needed, so that no roundoff or overflow occurs. For more information, see Full Precision for Fixed-Point System Objects.
Setting this property also sets the
NumeratorProductDataType property to the same
value.
Specify the product fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorProductDataType and
CustomDenominatorProductDataType properties
must have the same word lengths.
Dependencies
This property applies only when you set the
DenominatorProductDataType to
Custom.
Specify the numerator accumulator fixed-point data type as
Same as input, Same as
product, or Custom. Setting this property
also sets the DenominatorAccumulatorDataType
property to the same value.
Specify the numerator accumulator fixed-point type as a scaled
numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorAccumulatorDataType and
CustomDenominatorAccumulatorDataType properties
must have the same word lengths.
Dependencies
This property applies only when you set the
NumeratorAccumulatorDataType property to
Custom.
Specify the denominator accumulator fixed-point data type as
Same as input, Same as
product, or Custom. Setting this property
also sets the NumeratorAccumulatorDataType property
to the same value.
Specify the denominator accumulator fixed-point type as a scaled
numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorAccumulatorDataType and
CustomDenominatorAccumulatorDataType properties
must have the same word lengths.
Dependencies
This property applies only when you set the
DenominatorAccumulatorDataType property to
Custom.
Specify the state fixed-point data type as Same as
input, Same as accumulator, or
Custom.
Dependencies
This property applies when you set the Structure property to
Direct form II or Direct form II
transposed.
Specify the state fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of
Auto.
Dependencies
This property applies only when you set the
StateDataType property to
Custom.
Specify the numerator state fixed-point data type as Same as
input, Same as accumulator, or
Custom. Setting this property also sets the
DenominatorStateDataType property to the same
value.
Dependencies
This property applies only when you set the Structure property to
Direct form I transposed.
Specify the numerator state fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorProductDataType and
CustomDenominatorProductDataType properties
must have the same word lengths.
Dependencies
This property applies only when you set the
StateDataType property to
Custom.
Specify the denominator state fixed-point data type as Same
as input, Same as accumulator, or
Custom. Setting this property also sets the
NumeratorStateDataType property to the same
value.
Dependencies
This property applies only when you set the Structure property to
Direct form I transposed.
Specify the denominator state fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of Auto. The
CustomNumeratorStateDataType and
CustomDenominatorStateDataType properties must
have the same word lengths.
Dependencies
This property applies only when you set the
StateDataType property to
Custom.
Specify the output fixed-point data type as Same as
input, Same as accumulator, or
Custom.
Specify the output fixed-point type as a scaled numerictype (Fixed-Point Designer) object
with a Signedness of
Auto.
Dependencies
This property applies only when you set the OutputDataType property to
Custom.
Usage
Description
Input Arguments
Data input, specified as a vector or a matrix. This object also accepts variable-size inputs. Once the object is locked, you can change the size of each input channel, but you cannot change the number of channels.
The data type of all the inputs must be the same. If the input is fixed-point, it must be signed fixed point with power-of-two slope and zero bias.
The complexity of x, num,
and den must be the same.
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Complex Number Support: Yes
Numerator coefficients, specified as a 3-by-N
numeric matrix, where N is the number of biquad
filter sections. The complexity of x,
num, and den must be the
same.
The data type of all the inputs must be the same. If
num is fixed point, it must be signed fixed
point with power-of-two slope and zero bias.
Dependencies
This input applies only when you set SOSMatrixSource property is Input
port.
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Complex Number Support: Yes
Denominator coefficients, specified as a 2-by-N numeric matrix, where N is the number of biquad filter sections. The object assumes that the first denominator coefficient of each section is 1.
The data type of all the inputs must be the same. If
den is fixed point, it must be signed fixed
point with power-of-two slope and zero bias.
The complexity of x, num,
and den must be the same.
Dependencies
This input applies only when you set SOSMatrixSource property is Input
port.
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Complex Number Support: Yes
Scale values of the biquad filter, specified as a 1-by-(N
+1) numeric vector, where N is the number
of biquad filter sections.
The data type of all the inputs must be the same. If
g is fixed point, it must be signed fixed point
with power-of-two slope and zero bias.
Dependencies
This input applies when the SOSMatrixSource property is Input
Port and the ScaleValuesInputPort
property is true.
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Output Arguments
Filtered output, returned as a vector or a matrix. The size, data type, and complexity of the output signal matches that of the input signal.
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Complex Number Support: Yes
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
sos2ctf | Convert digital filter second-order section parameters to cascaded transfer function form |
freqz | Frequency response of discrete-time filter System object |
impz | Impulse response of discrete-time filter System object |
info | Information about filter System object |
coeffs | Returns the filter System object coefficients in a structure |
cost | Estimate cost of implementing filter System object |
scale | Scale second-order sections |
scaleopts | Create an options object for second-order section scaling |
scalecheck | Check scaling of biquadratic filter |
cumsec | Cumulative second-order section of the biquadratic filter |
tf | Convert discrete-time filter System object to transfer function |
reorder | Reorder second-order sections of biquadratic filter System object |
outputDelay | Determine output delay of single-rate or multirate filter |
Examples
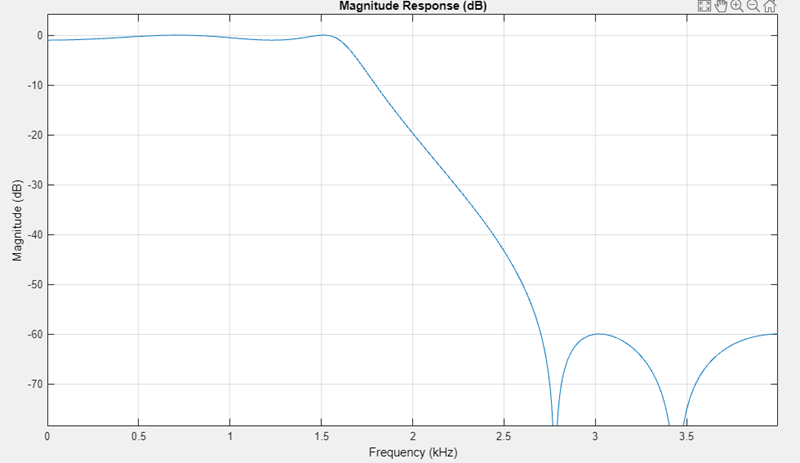
Use a fourth order, lowpass biquadratic filter object with a normalized cutoff frequency of 0.4 to filter high frequencies from an input signal. Display the result as a power spectrum using the Spectrum Analyzer.
t = (0:1000)'/8e3; % Input is 0.3 & % 3kHz sinusoids xin = sin(2*pi*0.3e3*t)+sin(2*pi*3e3*t); src = dsp.SignalSource(xin, 100); sink = dsp.SignalSink; % Set up the filter [z,p,k] = ellip(4,1,60,.4); [sosMatrix,scaleValues] = zp2sos(z,p,k); biquad = dsp.BiquadFilter(sosMatrix,... scaleValues,Structure="Direct form I"); sa = spectrumAnalyzer(SampleRate=8e3,... Method="welch",... PlotAsTwoSidedSpectrum=false,... OverlapPercent=80,SpectrumUnits="dBW",... YLimits=[-160 -10]); while ~isDone(src) input = src(); filteredOutput = biquad(input); sink(filteredOutput); sa(filteredOutput) end

filteredResult = sink.Buffer; fvtool(biquad,Fs=8000)
Demonstrate the Linf-norm scaling of a biquadratic SOS filter
using the scale function.
Fs = 8000; Fcutoff = 2000; [z,p,k] = butter(10,Fcutoff/(Fs/2)); [sosMatrix,scaleValues] = zp2sos(z,p,k); sosFilt = dsp.SOSFilter(Structure="Direct form I", ... Numerator=sosMatrix(:,1:3),Denominator=sosMatrix(:,4:6), ... HasScaleValues=true,ScaleValues=scaleValues)
sosFilt =
dsp.SOSFilter with properties:
Structure: "Direct form I"
CoefficientSource: "Property"
Numerator: [5x3 double]
Denominator: [5x3 double]
HasScaleValues: true
ScaleValues: [0.0029 1 1 1 1 1]
Use get to show all properties
scale(sosFilt,"linf",scalevalueconstraint="none",maxscalevalue=2)
More About
The following diagrams show the data types used in the dsp.BiquadFilter object when the input is fixed-point. For each
filter structure the object supports, the data types shown in the diagrams can be
set through the respective fixed-point properties of the object.
Direct Form I


The following diagram shows the data types for one section of the filter for fixed-point signals.

The following diagrams show the fixed-point data types between filter sections.
When the data is not optimized:

When you specify OptimizeUnityScaleValues to
true, and scale values to 1:

Direct Form I Transposed


The following diagram shows the data types for one section of the filter for fixed-point signals.

The dashed casts are omitted when you specify
OptimizeUnityScaleValues to true, and
scale values to 1.
The following diagrams show the fixed-point data types between filter sections.
When the data is not optimized:

When you specify OptimizeUnityScaleValues to
true, and scale values to 1:

Direct Form II


The following diagram shows the data types for one section of the filter for fixed-point signals.

The dashed casts are omitted when you specify
OptimizeUnityScaleValues to true, and
scale values to 1.
The following diagrams show the fixed-point data types between filter sections.
When the data is not optimized:

When you specify OptimizeUnityScaleValues to
true, and scale values to 1:

Direct Form II Transposed


The following diagram shows the data types for one section of the filter for fixed-point signals.

The following diagrams show the fixed-point data types between filter sections.
When the data is not optimized:

When you specify OptimizeUnityScaleValues to
true, and scale values to 1:

Algorithms
This object implements the algorithm, inputs, and outputs described on the Biquad Filter block reference page. The object properties correspond to the block parameters, except:
Coefficient source
Action when the a0 values of the SOS matrix are not one – the biquad filter object assumes the zero-th-order denominator coefficient equals 1 regardless of the specified value. The biquad filter object does not support the
ErrororWarnoptions found in the corresponding block.
Both this object and its corresponding block support variable-size input. When you call the object, it can handle an input argument which is changing in size.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
For workflows and limitations, see HDL Code Generation for System Objects (HDL Coder).
Note
For a hardware-optimized biquad filter algorithm that supports HDL code
generation, use the dsphdl.BiquadFilter (DSP HDL Toolbox)
System object. This object has hardware-friendly valid and reset control
signals, and models exact hardware latency behavior. The DSP HDL Toolbox™
System object does not support programmable coefficients. The object supports
HDL code generation with HDL Coder™ tools.
Version History
Introduced in R2012aStarting in R2025a, the Filter Design HDL Coder™ product is discontinued. So, this object no longer supports HDL code
generation by using the generatehdl function. The object still
supports code generation using HDL Coder tools.
The dsp.BiquadFilter object issues a warning and it will be
removed in a future release. Use the dsp.SOSFilter object instead.
Update Code
This table shows how to replace the dsp.BiquadFilter object with
the dsp.SOSFilter object in a typical workflow.
| Discouraged Usage | Recommended Replacement |
|---|---|
[z,p,k] = ellip(4,1,60,0.4); [sosMatrix,scaleValues] = zp2sos(z,p,k); biquad = dsp.BiquadFilter(... SOSMatrix = sosMatrix,... ScaleValues = scaleValues,... Structure = "Direct form I"); |
[z,p,k] = ellip(4,1,60,0.4); [sosMatrix,scaleValues] = zp2sos(z,p,k); [num,den] = sos2ctf(sosMatrix); sosFilter = dsp.SOSFilter(num,den,... ScaleValues=scaleValues,... Structure="Direct form I"); |
[num,den] = designLowpassIIR(FilterOrder=20); x = randn(1000,1); biquad = dsp.BiquadFilter(... SOSMatrixSource="Input port",... Structure = "Direct form I",... ScaleValuesInputPort = false); Transpose the numerator coefficients array
designed by the num_biquad = num.'; Remove
the first column in the denominator coefficients array and
transpose the remaining elements before passing the array to the
den_biquad = den(:,2:end).'; y = biquad(x,num_biquad,den_biquad); |
[num,den] = designLowpassIIR(FilterOrder=20); x = randn(1000,1); sosFilter = dsp.SOSFilter(... CoefficientSource="Input port",... Structure = "Direct form I"); y = sosFilter(x,num,den); |
HDL Code Generation Support
For a replacement IIR filter that supports HDL code generation, use the dsphdl.BiquadFilter (DSP HDL Toolbox) object and generate code using HDL Coder tools.
Instead of specifying the SOS matrix, specify filter coefficients as
Numerator and Denominator matrices.
The object provides these hardware-optimized architecture options:
"Direct form II"and"Direct form II transposed"architectures are pipelined and quantized to fit well into FPGA DSP blocks."Pipelined feedback form"implements a pipelined architecture that uses more multipliers than either direct form II structure, but achieves higher clock rates after synthesis."Direct form I fully serial"implements a fully serial architecture that uses only one multiplier.
For an example, see Generate HDL Code for IIR Filter (DSP HDL Toolbox).
The dsp.BiquadFilter object will be removed in a future release.
Use the dsp.SOSFilter object instead.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)