dsp.AnalyticSignal
Analytic signals of discrete-time inputs
Description
The dsp.AnalyticSignal
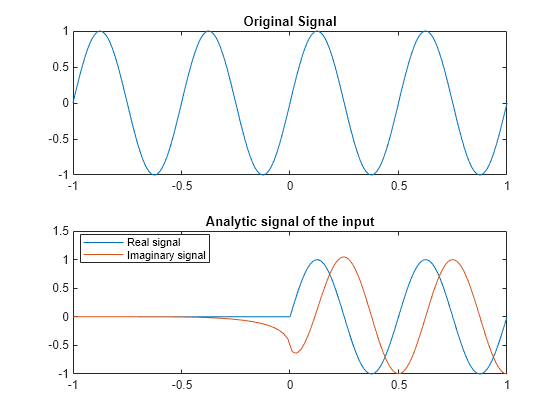
System object™ computes analytic signals of discrete-time inputs. The real part of the analytic
signal in each channel is a replica of the real input in that channel, and the imaginary part
is the Hilbert transform of the input. In the frequency domain, the analytic signal doubles
the positive frequency content of the original signal while zeroing-out negative frequencies
and retaining the DC component.
The object computes the Hilbert transform using an equiripple FIR filter or a Kaiser window FIR filter. When the filter order is low, the object uses an equiripple FIR filter. For higher filter orders, if the equiripple design fails, the object uses a Kaiser window FIR filter.
To compute the analytic signal of a discrete-time input:
Create the
dsp.AnalyticSignalobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
This object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.
Creation
Syntax
Description
anaSig = dsp.AnalyticSignalanaSig, that computes the complex analytic
signal corresponding to each channel of a real
M-by-N input matrix.
anaSig = dsp.AnalyticSignal(order)anaSig, with the FilterOrder property set to
order.
anaSig = dsp.AnalyticSignal(Name=Value)FilterOrder to 24.
Properties
Usage
Syntax
Description
y = anaSig(x)y, of the
M-by-N input matrix x,
according to the equation
where j is the imaginary unit and denotes the Hilbert transform.
Each of the N columns in x contains
M sequential time samples from an independent channel. The method
computes the analytic signal for each channel.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
Algorithms
The algorithm computes the Hilbert transform with an equiripple FIR for the specified order n using the Remez exchange algorithm. For higher filter orders, if the equiripple design fails, the algorithm uses a Kaiser window FIR filter instead. In both cases, the filter has a linear phase with a constant group delay of n/2 input samples.