Build Time Series Forecasting Network Using Deep Network Designer
This example shows how to create a simple long short-term memory (LSTM) network to forecast time series data using the Deep Network Designer app.
An LSTM network is a recurrent neural network (RNN) that processes input data by looping over time steps and updating the RNN state. The RNN state contains information remembered over all previous time steps. You can use an LSTM neural network to forecast subsequent values of a time series or sequence using previous time steps as input. To create an LSTM network for time series forecasting, use the Deep Network Designer app.
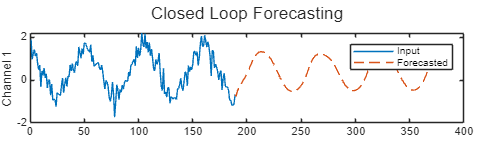
This figure shows an example sequence with forecasted values using closed loop prediction.
Load Sequence Data
Load the example data from WaveformData. To access this data, open the example as a live script. The Waveform data set contains synthetically generated waveforms of varying lengths with three channels. This example trains an LSTM neural network to forecast future values of the waveforms given the values from previous time steps.
load WaveformDataView the sizes of the first few sequences.
data(1:4)
ans=4×1 cell array
{103×3 double}
{136×3 double}
{140×3 double}
{124×3 double}
View the number of channels. To train the LSTM neural network, each sequence must have the same number of channels.
numChannels = size(data{1},2)numChannels = 3
Visualize some of the sequences.
idx = 1;
numChannels = size(data{idx},2);
figure
stackedplot(data{idx},DisplayLabels="Channel " + (1:numChannels))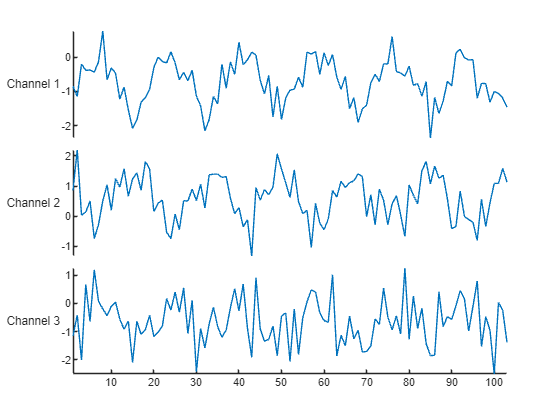
Prepare Data for Training
To forecast the values of future time steps of a sequence, specify the targets as the training sequences with values shifted by one time step. Do not include the final time step in the training sequences. In other words, at each time step of the input sequence, the LSTM neural network learns to predict the value of the next time step. The predictors are the training sequences without the final time step.
numObservations = numel(data); XData = cell(numObservations,1); TData = cell(numObservations,1); for n = 1:numObservations X = data{n}; XData{n} = X(1:end-1,:); TData{n} = X(2:end,:); end
Partition the data into training, validation, and test sets. Use 80% of the data for training, 10% for validation, and 10% for testing. To partition the data, use the trainingPartitions function, attached to this example as a supporting file. To access this file, open the example as a live script.
[idxTrain,idxValidation,idxTest] = trainingPartitions(numObservations,[0.8 0.1 0.1]); XTrain = XData(idxTrain); TTrain = TData(idxTrain); XValidation = XData(idxValidation); TValidation = TData(idxValidation); XTest = XData(idxTest); TTest = TData(idxTest);
For a better fit and to prevent the training from diverging, normalize the predictors and targets so that the channels have zero mean and unit variance. When you make predictions, you must also normalize the validation and test data using the same statistics as the training data.
Calculate the per-channel mean and standard deviation values for the sequences. To easily calculate the mean and standard deviation for the training data, create numeric arrays that contains the concatenated sequences using the cell2mat function.
muX = mean(cell2mat(XTrain)); sigmaX = std(cell2mat(XTrain),0); muT = mean(cell2mat(TTrain)); sigmaT = std(cell2mat(TTrain),0);
Normalize the training data using the calculated mean and standard deviation values.
for n = 1:numel(XTrain) XTrain{n} = (XTrain{n} - muX) ./ sigmaX; TTrain{n} = (TTrain{n} - muT) ./ sigmaT; end
Normalize the validation and test data using the statistics calculated from the training data.
for n = 1:numel(XValidation) XValidation{n} = (XValidation{n} - muX) ./ sigmaX; TValidation{n} = (TValidation{n} - muT) ./ sigmaT; end for n = 1:numel(XTest) XTest{n} = (XTest{n} - muX) ./ sigmaX; TTest{n} = (TTest{n} - muT) ./ sigmaT; end
Define Network Architecture
To build the network, open the Deep Network Designer app.
deepNetworkDesigner
To create a sequence network, in the Sequence-to-Sequence Classification Networks (Untrained) section, click LSTM.
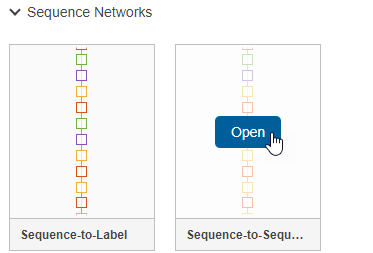
Doing so opens a prebuilt network suitable for sequence classification problems. The network contains these layers:
sequenceInputLayerlstmLayerdropoutLayerfullyConnectedLayersoftmaxLayer
You can convert the classification network into a network suitable for time series forecasting by editing the final layers. First, delete the softmax layer.
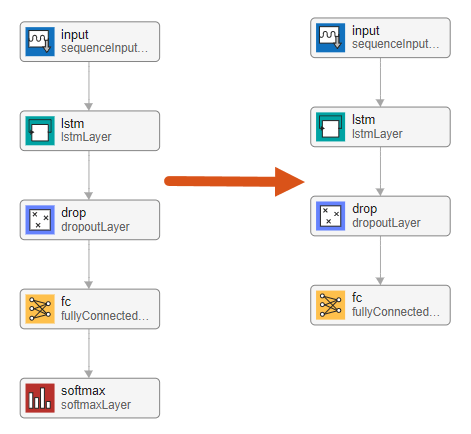
Next, adjust the properties of the layers so that they are suitable for the Waveform data set. Because the aim is to forecast future data points in a time series, the output size must be the same as the input size. In this example, the input data has three input channels so, the network output must also have three output channels.
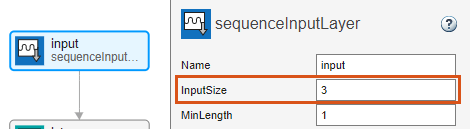
Select the sequence input layer input and set InputSize to 3.
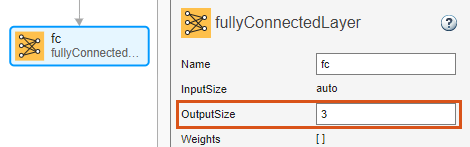
Select the fully connected layer fc and set OutputSize to 3.
The LSTM layer has 128 hidden units. The number of hidden units determines how much information is learned by the layer. Using more hidden units can yield more accurate results but can be more likely to lead to overfitting to the training data. The dropout layer helps to avoid overfitting by randomly setting inputs to the layer to zero and effectively changing the network architecture between training iterations. A higher dropout probability can improve model generalization at the cost of losing information and slowing down the learning process.
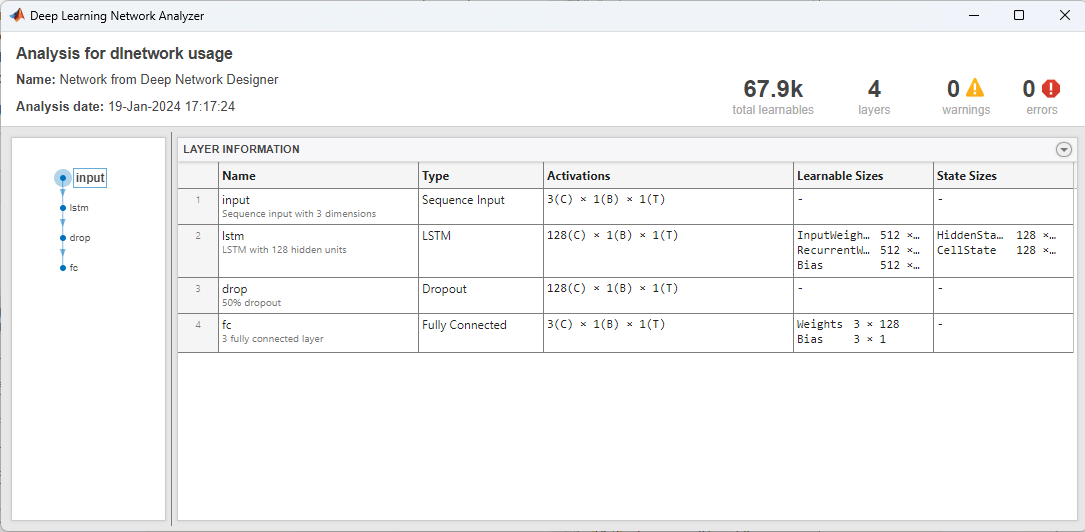
To check that the network is ready for training, click Analyze. The Deep Learning Network Analyzer reports zero errors or warnings, so the network is ready for training. To export the network, click Export. The app saves the network in the variable net_1.
Specify Training Options
Specify the training options. Choosing among the options requires empirical analysis. To explore different training option configurations by running experiments, you can use the Experiment Manager app.
Train using Adam optimization.
Train for 200 epochs. For larger data sets, you might not need to train for as many epochs for a good fit.
In each mini-batch, left-pad the sequences so they have the same length. Left-padding prevents the RNN from predicting padding values at the ends of sequences.
Shuffle the data every epoch.
Monitor overfitting using validation data.
Monitor the root mean square error.
Display the training progress in a plot.
Disable the verbose output.
options = trainingOptions("adam", ... MaxEpochs=200, ... SequencePaddingDirection="left", ... Shuffle="every-epoch", ... ValidationData={XValidation,TValidation}, ... Metrics="rmse", ... Plots="training-progress", ... Verbose=false);
Train Neural Network
Train the LSTM neural network using the trainnet function. For regression, use mean squared error loss. By default, the trainnet function uses a GPU if one is available. Using a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the function uses the CPU. To specify the execution environment, use the ExecutionEnvironment training option.
net = trainnet(XTrain,TTrain,net_1,"mse",options);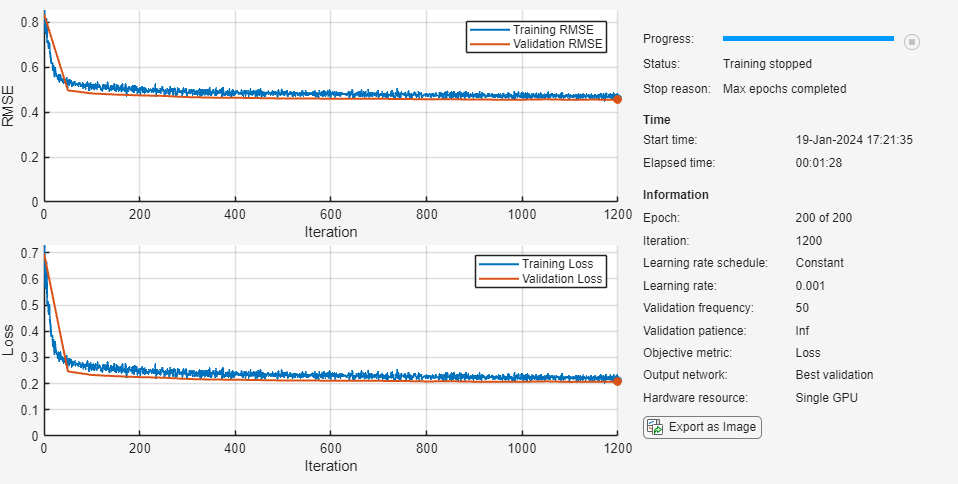
Test Recurrent Neural Network
Make predictions using the minibatchpredict function. By default, the minibatchpredict function uses a GPU if one is available. Pad the sequences using the same padding options as for training. For sequence-to-sequence tasks with sequences of varying lengths, return the predictions as a cell array by setting the UniformOutput option to false.
YTest = minibatchpredict(net,XTest, ... SequencePaddingDirection="left", ... UniformOutput=false);
For each test sequence, calculate the root mean squared error (RMSE) between the predictions and targets. Ignore any padding values by removing these before computing the RMSE.
numObservationsTest = numel(XTest); for n = 1:numObservationsTest T = TTest{n}; sequenceLength = size(T,1); Y = YTest{n}(end-sequenceLength+1:end,:); err(n) = rmse(Y,T,"all"); end
Visualize the errors in a histogram. Lower values indicate greater accuracy.
figure histogram(err) xlabel("RMSE") ylabel("Frequency")
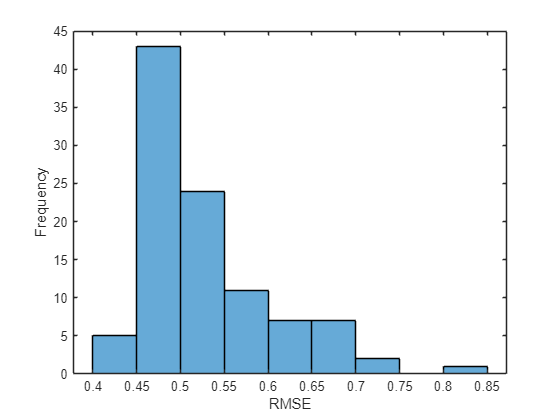
Calculate the mean RMSE over all test observations.
mean(err,"all")ans = single
0.5304
Forecast Future Time Steps
Given an input time series or sequence, to forecast the values of multiple future time steps, use the predict function to predict time steps one at a time and update the RNN state at each prediction. For each prediction, use the previous prediction as the input to the function.
Visualize one of the test sequences in a plot.
idx = 3;
X = XTest{idx};
T = TTest{idx};
figure
stackedplot(X,DisplayLabels="Channel " + (1:numChannels))
xlabel("Time Step")
title("Test Observation " + idx)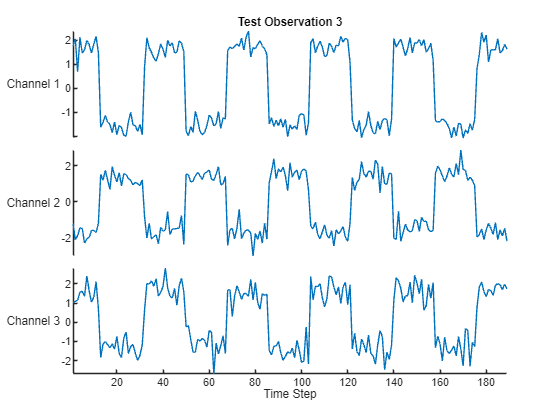
There are two methods of forecasting: open loop and closed loop forecasting.
Open loop forecasting — Predict the next time step in a sequence using only the input data. When making predictions for subsequent time steps, you collect the true values from your data source and use those as input. For example, say you want to predict the value for time step of a sequence using data collected in time steps 1 through . To make predictions for time step , wait until you record the true value for time step and use that as input to make the next prediction. Use open loop forecasting when you have true values to provide to the RNN before making the next prediction.
Closed loop forecasting — Predict subsequent time steps in a sequence by using the previous predictions as input. In this case, the model does not require the true values to make the prediction. For example, say you want to predict the values for time steps through of the sequence using data collected in time steps 1 through only. To make predictions for time step , use the predicted value for time step as input. Use closed loop forecasting to forecast multiple subsequent time steps or when you do not have the true values to provide to the RNN before making the next prediction.
Open Loop Forecasting
Perform open loop forecasting.
Initialize the RNN state by first resetting the state using the resetState function, then make an initial prediction using the first few time steps of the input data. Update the RNN state using the first 75 time steps of the input data.
net = resetState(net); offset = 75; [Z,state] = predict(net,X(1:offset,:)); net.State = state;
To forecast further predictions, loop over time steps and make predictions using the predict function. After each prediction, update the RNN state. Forecast values for the remaining time steps of the test observation by looping over the time steps of the input data and using them as input to the RNN. The last time step of the initial prediction is the first forecasted time step.
numTimeSteps = size(X,1); numPredictionTimeSteps = numTimeSteps - offset; Y = zeros(numPredictionTimeSteps,numChannels); Y(1,:) = Z(end,:); for t = 1:numPredictionTimeSteps-1 Xt = X(offset+t,:); [Y(t+1,:),state] = predict(net,Xt); net.State = state; end
Compare the predictions with the input values.
figure t = tiledlayout(numChannels,1); title(t,"Open Loop Forecasting") for i = 1:numChannels nexttile plot(X(:,i)) hold on plot(offset:numTimeSteps,[X(offset,i) Y(:,i)'],"--") ylabel("Channel " + i) end xlabel("Time Step") nexttile(1) legend(["Input" "Forecasted"])
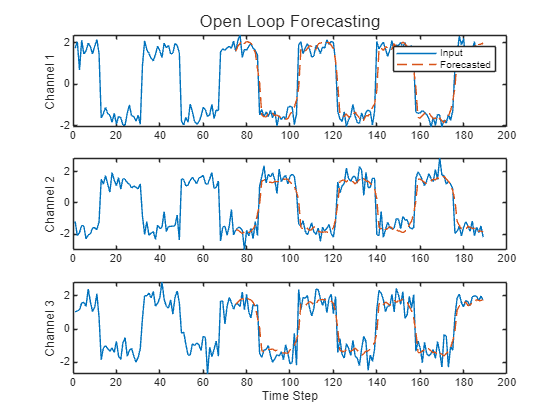
Closed Loop Forecasting
Perform close loop forecasting.
Initialize the RNN state by first resetting the state using the resetState function, then make an initial prediction Z using the first few time steps of the input data. Update the RNN state using all time steps of the input data.
net = resetState(net); offset = size(X,1); [Z,state] = predict(net,X(1:offset,:)); net.State = state;
To forecast further predictions, loop over time steps and make predictions using the predict function. After each prediction, update the RNN state. Forecast the next 200 time steps by iteratively passing the previous predicted value to the RNN. Because the RNN does not require the input data to make any further predictions, you can specify any number of time steps to forecast. The last time step of the initial prediction is the first forecasted time step.
numPredictionTimeSteps = 200; Y = zeros(numPredictionTimeSteps,numChannels); Y(1,:) = Z(end,:); for t = 2:numPredictionTimeSteps [Y(t,:),state] = predict(net,Y(t-1,:)); net.State = state; end
Visualize the forecasted values in a plot.
numTimeSteps = offset + numPredictionTimeSteps; figure t = tiledlayout(numChannels,1); title(t,"Closed Loop Forecasting") for i = 1:numChannels nexttile plot(X(1:offset,i)) hold on plot(offset:numTimeSteps,[X(offset,i) Y(:,i)'],"--") ylabel("Channel " + i) end xlabel("Time Step") nexttile(1) legend(["Input" "Forecasted"])

Closed loop forecasting allows you to forecast an arbitrary number of time steps, but can be less accurate when compared to open loop forecasting because the RNN does not have access to the true values during the forecasting process.