Remaining Useful Life Estimation Using Convolutional Neural Network
This example shows how to predict the remaining useful life (RUL) of engines by using deep convolutional neural networks (CNNs) [1]. The advantage of a deep learning approach is that you do not need manual feature extraction or feature selection for your model to predict RUL. Furthermore, you do not need prior knowledge of machine health prognostics or signal processing to develop a deep learning based RUL prediction model.
Download Data Set
This example uses the Turbofan Engine Degradation Simulation data set [1]. The data set is in ZIP file format, and contains run-to-failure time-series data for four different sets (namely FD001, FD002, FD003, and FD004) simulated under different combinations of operational conditions and fault modes.
This example uses only the FD001 data set, which is further divided into training and test subsets. The training subset contains simulated time series data for 100 engines. Each engine has several sensors whose values are recorded at a given instance in a continuous process. Hence, the sequence of recorded data varies in length and corresponds to a full run-to-failure (RTF) instance. The test subset contains 100 partial sequences and corresponding values of the remaining useful life at the end of each sequence.
Create a directory to store the Turbofan Engine Degradation Simulation data set.
dataFolder = "data"; if ~exist(dataFolder,'dir') mkdir(dataFolder); end
Download and extract the Turbofan Engine Degradation Simulation data set.
filename = matlab.internal.examples.downloadSupportFile("nnet","data/TurbofanEngineDegradationSimulationData.zip"); unzip(filename,dataFolder)
The data folder now contains text files with 26 columns of numbers, separated by spaces. Each row is a snapshot of data taken during a single operational cycle, and each column represents a different variable:
Column 1 — Unit number
Column 2 — Timestamp
Columns 3–5 — Operational settings
Columns 6–26 — Sensor measurements 1–21
Preprocess Training Data
Load the data using the function localLoadData. The function extracts the data from a data file and returns a table which contains the training predictors and corresponding response (i.e., RUL) sequences. Each row represents a different engine.
filenameTrainPredictors = fullfile(dataFolder,"train_FD001.txt");
rawTrain = localLoadData(filenameTrainPredictors);Examine the run-to-failure data for one of the engines.
head(rawTrain.X{1},8) id timeStamp op_setting_1 op_setting_2 op_setting_3 sensor_1 sensor_2 sensor_3 sensor_4 sensor_5 sensor_6 sensor_7 sensor_8 sensor_9 sensor_10 sensor_11 sensor_12 sensor_13 sensor_14 sensor_15 sensor_16 sensor_17 sensor_18 sensor_19 sensor_20 sensor_21
__ _________ ____________ ____________ ____________ ________ ________ ________ ________ ________ ________ ________ ________ ________ _________ _________ _________ _________ _________ _________ _________ _________ _________ _________ _________ _________
1 1 -0.0007 -0.0004 100 518.67 641.82 1589.7 1400.6 14.62 21.61 554.36 2388.1 9046.2 1.3 47.47 521.66 2388 8138.6 8.4195 0.03 392 2388 100 39.06 23.419
1 2 0.0019 -0.0003 100 518.67 642.15 1591.8 1403.1 14.62 21.61 553.75 2388 9044.1 1.3 47.49 522.28 2388.1 8131.5 8.4318 0.03 392 2388 100 39 23.424
1 3 -0.0043 0.0003 100 518.67 642.35 1588 1404.2 14.62 21.61 554.26 2388.1 9052.9 1.3 47.27 522.42 2388 8133.2 8.4178 0.03 390 2388 100 38.95 23.344
1 4 0.0007 0 100 518.67 642.35 1582.8 1401.9 14.62 21.61 554.45 2388.1 9049.5 1.3 47.13 522.86 2388.1 8133.8 8.3682 0.03 392 2388 100 38.88 23.374
1 5 -0.0019 -0.0002 100 518.67 642.37 1582.8 1406.2 14.62 21.61 554 2388.1 9055.1 1.3 47.28 522.19 2388 8133.8 8.4294 0.03 393 2388 100 38.9 23.404
1 6 -0.0043 -0.0001 100 518.67 642.1 1584.5 1398.4 14.62 21.61 554.67 2388 9049.7 1.3 47.16 521.68 2388 8132.9 8.4108 0.03 391 2388 100 38.98 23.367
1 7 0.001 0.0001 100 518.67 642.48 1592.3 1397.8 14.62 21.61 554.34 2388 9059.1 1.3 47.36 522.32 2388 8132.3 8.3974 0.03 392 2388 100 39.1 23.377
1 8 -0.0034 0.0003 100 518.67 642.56 1583 1401 14.62 21.61 553.85 2388 9040.8 1.3 47.24 522.47 2388 8131.1 8.4076 0.03 391 2388 100 38.97 23.311
Examine the response data for one of the engines.
rawTrain.Y{1}(1:8)ans = 8×1
191
190
189
188
187
186
185
184
Visualize the time-series data for some of the predictors.
stackedplot(rawTrain.X{1},[3,5,6,7,8,15,16,24],XVariable='timeStamp')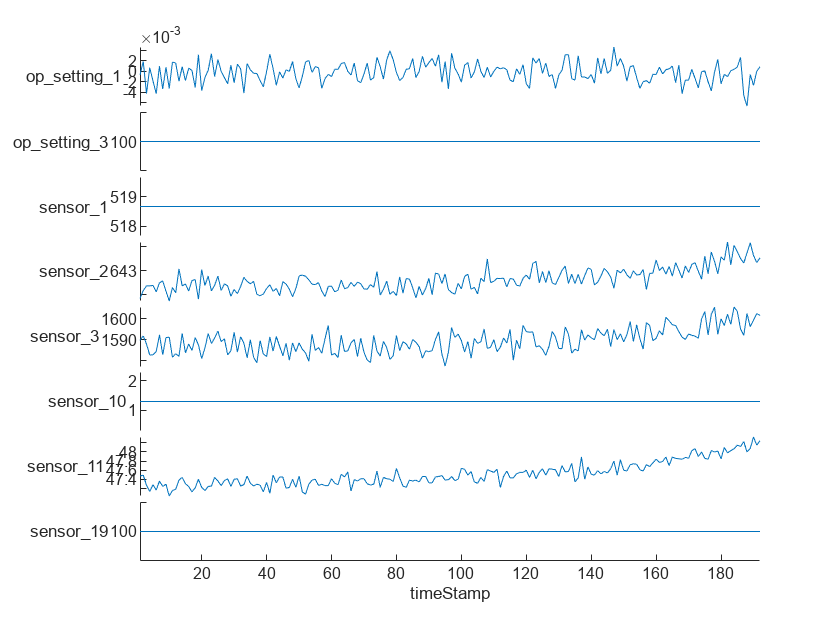
Remove Features with Less Variability
Features that remain constant for all time steps can negatively impact the training. Use the prognosability (Predictive Maintenance Toolbox) function to measure the variability of features at failure.
prog = prognosability(rawTrain.X,"timeStamp");For some features, prognosability is equal to zero or NaN. Discard these features.
idxToRemove = prog.Variables==0 | isnan(prog.Variables); featToRetain = prog.Properties.VariableNames(~idxToRemove); for i = 1:height(rawTrain) rawTrain.X{i} = rawTrain.X{i}{:,featToRetain}; end
Normalize Training Predictors
Normalize the training predictors to have zero mean and unit variance.
[~,Xmu,Xsigma] = zscore(vertcat(rawTrain.X{:}));
preTrain = table();
for i = 1:numel(rawTrain.X)
preTrain.X{i} = (rawTrain.X{i} - Xmu) ./ Xsigma;
endClip Responses
The response data represents the RUL value over life for each engine and is based individual engine lifetime. The sequence assumes a linear degradation from the time of the initial measurement to the time of engine failure.
In order for network to focus on the part of the data where engines are more likely to fail (end of the engine's life), clip the responses at the threshold of 150. Clipping the responses causes the network to treat instances with higher RUL values as equal.
rulThreshold = 150; for i = 1:numel(rawTrain.Y) preTrain.Y{i} = min(rawTrain.Y{i},rulThreshold); end
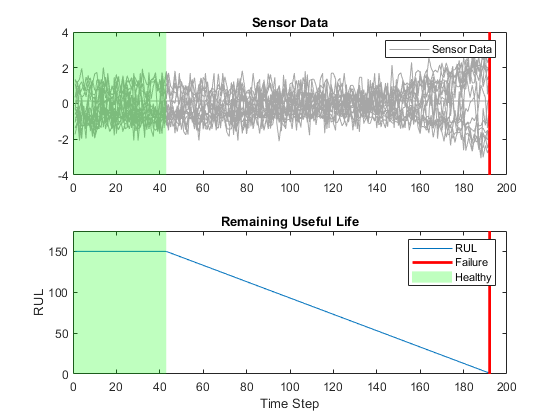
This figure shows the first observation and the corresponding response (RUL), which is clipped at the threshold. The green overlay defines the clipping region on both sensor amd RUL plots.
Prepare Data for Padding
This network supports input data with varying sequence lengths. When passing data through the network, the software pads, truncates, or splits sequences so that all the sequences in each mini-batch have the specified length.
To minimize the amount of padding added to the mini-batches, sort the training data by sequence length. Then, choose a mini-batch size which divides the training data evenly and reduces the amount of padding in the mini-batches.
Sort the training data by sequence length.
for i = 1:size(preTrain,1) preTrain.X{i} = preTrain.X{i}'; %Transpose training data to have features in the first dimension preTrain.Y{i} = preTrain.Y{i}'; %Transpose responses corresponding to the training data sequence = preTrain.X{i}; sequenceLengths(i) = size(sequence,2); end [sequenceLengths,idx] = sort(sequenceLengths,'descend'); XTrain = preTrain.X(idx); YTrain = preTrain.Y(idx);
Network Architecture
The deep convolutional neural network architecture used for RUL estimation is described in [1].
Here, you process and sort the data in a sequence format, with the first dimension representing the number of selected features and the second dimension representing the length of the time sequence. You bundle convolutional layers with batch normalization layer followed by an activation layer (relu in this case) and then stack the layers together for feature extraction. The fully connected layers are used at the end to get the final RUL value as output.
The selected network architecture applies a 1-D convolution along the time sequence direction only. Therefore, the order of features does not impact the training and only trends in one feature at a time are considered.
Define the network architecture. Create a CNN that consists of five consecutive sets of a convolution 1-d, batch normalization, and a relu layer, with increasing filterSize and numFilters as the first two input arguments to convolution1dLayer, followed by a fully connected layer of size numHiddenUnits and a dropout layer with a dropout probability of 0.5. Since the network predicts the remaining useful life (RUL) of the turbofan engine, set numResponses to 1 in the second fully connected layer.
To compensate for the varying time-sequences in the training data, use Padding="causal" as the Name-value pair input argument in convolution1dLayer.
numFeatures = size(XTrain{1},1);
numHiddenUnits = 100;
numResponses = 1;
layers = [
sequenceInputLayer(numFeatures)
convolution1dLayer(5,32,Padding="causal")
batchNormalizationLayer
reluLayer()
convolution1dLayer(7,64,Padding="causal")
batchNormalizationLayer
reluLayer()
convolution1dLayer(11,128,Padding="causal")
batchNormalizationLayer
reluLayer()
convolution1dLayer(13,256,Padding="causal")
batchNormalizationLayer
reluLayer()
convolution1dLayer(15,512,Padding="causal")
batchNormalizationLayer
reluLayer()
fullyConnectedLayer(numHiddenUnits)
reluLayer()
dropoutLayer(0.5)
fullyConnectedLayer(numResponses)];Train Network
Specify trainingOptions. Train for 40 epochs with minibatches of size 16 using the Adam optimizer. Set LearnRateSchedule to piecewise. Specify the learning rate as 0.01. To prevent the gradients from exploding, set the gradient threshold to 1. To keep the sequences sorted by length, set 'Shuffle' to 'never'. Turn on the training progress plot and also set the Metrics to 'rmse' to view the RMSE plot. Set the InputDataFormats as CTB because the training data contains features in the first dimension, time-series sequence in the second dimension, and the batches of the data in the third dimension. Turn off the command window output (Verbose).
maxEpochs = 40; miniBatchSize = 16; options = trainingOptions('adam',... LearnRateSchedule='piecewise',... MaxEpochs=maxEpochs,... MiniBatchSize=miniBatchSize,... InitialLearnRate=0.01,... GradientThreshold=1,... Shuffle='never',... Plots='training-progress',... Metrics='rmse',... InputDataFormats='CTB',... Verbose=0);
Train the network using trainnet and specify the loss function as mean squared error (mse). This should take about 1-2 minutes.
net = trainnet(XTrain,YTrain,layers,"mse",options);
Plot the layer graph of the network to visualize the underlying network architecture.
figure; plot(net)

Test Network
The test data contains 100 partial sequences and corresponding values of the remaining useful life at the end of each sequence.
filenameTestPredictors = fullfile(dataFolder,'test_FD001.txt'); filenameTestResponses = fullfile(dataFolder,'RUL_FD001.txt'); dataTest = localLoadData(filenameTestPredictors,filenameTestResponses);
Prepare the test data set for predictions by performing the same preprocessing steps you use to prepare the training data set.
for i = 1:numel(dataTest.X) dataTest.X{i} = dataTest.X{i}{:,featToRetain}; dataTest.X{i} = (dataTest.X{i} - Xmu) ./ Xsigma; dataTest.Y{i} = min(dataTest.Y{i},rulThreshold); end
Create a table for storing the predicted response (YPred) along with the true response (Y). Make predictions on the test data using minibatchpredict. To prevent the function from adding padding to the test data, specify the mini-batch size as 1 to get RUL value for each observation in the test data. Set InputDataFormats as CTB because the test data is also in the same format as the training data.
predictions = table(Size=[height(dataTest) 2],VariableTypes=["cell","cell"],VariableNames=["Y","YPred"]); for i=1:height(dataTest) unit = dataTest.X{i}'; predictions.Y{i} = dataTest.Y{i}'; predictions.YPred{i} = minibatchpredict(net,unit,MiniBatchSize=1,InputDataFormats='CTB'); end
Performance Metrics
Compute the root mean squared error (RMSE) across all time cycles of the test sequences to analyze how well the network performs on the test data.
for i = 1:size(predictions,1) predictions.RMSE(i) = sqrt(mean((predictions.Y{i} - predictions.YPred{i}).^2)); end
Create a histogram to visualize the distribution of RMSE values across all test engines.
figure; histogram(predictions.RMSE,NumBins=10); title("RMSE ( Mean: " + round(mean(predictions.RMSE),2) + " , StDev: " + round(std(predictions.RMSE),2) + " )"); ylabel('Frequency'); xlabel('RMSE');

Additionally, to see how the network predictor performs throughout the given sequence of data in the test engines, use the localLambdaPlot function to plot the predicted RUL against the true RUL of a random test engine.
figure;
localLambdaPlot(predictions,"random");
The result shows that the CNN deep learning architecture for estimating RUL of the turbo engine data is a viable approach to predict RUL. The RMSE values at all timestamps indicates that the network can perform well towards the end of the given test sequence data. Therefore, having a brief history of the sensor data is important when trying to predict RUL.
Helper Functions
Load Data Function
This function loads run-to-failure data from the provided text file and groups time-series data and its corresponding RUL values in a table as predictors and responses.
function data = localLoadData(filenamePredictors,varargin) if isempty(varargin) filenameResponses = []; else filenameResponses = varargin{:}; end %% Load the text file as a table rawData = readtable(filenamePredictors); % Add variable names to the table VarNames = {... 'id', 'timeStamp', 'op_setting_1', 'op_setting_2', 'op_setting_3', ... 'sensor_1', 'sensor_2', 'sensor_3', 'sensor_4', 'sensor_5', ... 'sensor_6', 'sensor_7', 'sensor_8', 'sensor_9', 'sensor_10', ... 'sensor_11', 'sensor_12', 'sensor_13', 'sensor_14', 'sensor_15', ... 'sensor_16', 'sensor_17', 'sensor_18', 'sensor_19', 'sensor_20', ... 'sensor_21'}; rawData.Properties.VariableNames = VarNames; if ~isempty(filenameResponses) RULTest = readmatrix(filenameResponses); end % Split the signals for each unit ID IDs = rawData{:,1}; nID = unique(IDs); numObservations = numel(nID); % Initialize a table for storing data data = table(Size=[numObservations 2],... VariableTypes={'cell','cell'},... VariableNames={'X','Y'}); for i=1:numObservations idx = IDs == nID(i); data.X{i} = rawData(idx,:); if isempty(filenameResponses) % Calculate RUL from time column for train data data.Y{i} = flipud(rawData.timeStamp(idx))-1; else % Use RUL values from filenameResponses for test data sequenceLength = sum(idx); endRUL = RULTest(i); data.Y{i} = [endRUL+sequenceLength-1:-1:endRUL]'; %#ok<NBRAK> end end end
Lambda Plot function
This helper function accepts the predictions table and a lambdaCase argument, and plots the predicted RUL against the true RUL throughout its sequence (at every timestamp) for a visualization of how the prediction changes with every timestamp. The second argument, lambdaCase, can be the test engine number or one of a set of valid strings to find an engine number: "random", "best", "worst", or "average".
function localLambdaPlot(predictions,lambdaCase) if isnumeric(lambdaCase) idx = lambdaCase; else switch lambdaCase case {"Random","random","r"} idx = randperm(height(predictions),1); % Randomly choose a test case to plot case {"Best","best","b"} idx = find(predictions.RMSE == min(predictions.RMSE)); % Best case case {"Worst","worst","w"} idx = find(predictions.RMSE == max(predictions.RMSE)); % Worst case case {"Average","average","a"} err = abs(predictions.RMSE-mean(predictions.RMSE)); idx = find(err==min(err),1); end end y = predictions.Y{idx}; yPred = predictions.YPred{idx}; x = 0:numel(y)-1; plot(x,y,x,yPred) legend("True RUL","Predicted RUL") xlabel("Time stamp (Test data sequence)") ylabel("RUL (Cycles)") title("RUL for Test engine #"+idx+ " ("+lambdaCase+" case)") end
References
Li, Xiang, Qian Ding, and Jian-Qiao Sun. “Remaining Useful Life Estimation in Prognostics Using Deep Convolution Neural Networks.” Reliability Engineering & System Safety 172 (April 2018): 1–11. https://doi.org/10.1016/j.ress.2017.11.021.
See Also
imageInputLayer | prognosability (Predictive Maintenance Toolbox) | trainingOptions
Topics
- Learn About Convolutional Neural Networks
- Sequence-to-Sequence Regression Using Deep Learning
- Similarity-Based Remaining Useful Life Estimation (Predictive Maintenance Toolbox)