Parameter Pruning and Quantization of Image Classification Network

This example shows how to prune the parameters of a trained neural network by using unstructured pruning.

In many applications where you use transfer learning to retrain an image classification network for a new task or where you train a new network from scratch, you do not know the optimal network architecture, and the network can be overparameterized. An overparameterized network has redundant connections. Pruning identifies redundant connections that you can remove without affecting the network accuracy.

This example uses unstructured pruning to increase the number of parameters with a value of zero based on two parameter score metrics: magnitude score [1] and Synaptic Flow score [2]. Increasing the number of parameters with a value of zero increases the sparsity of the network.

This example shows how to:

• Perform post-training, iterative, unstructured pruning without the need for training data

• Evaluate the performance of two different pruning algorithms

• Investigate the layer-wise sparsity induced after pruning

• Evaluate the impact of pruning on classification accuracy

• Evaluate the impact of quantization on the classification accuracy of the pruned network

This example uses a simple convolutional neural network to classify user-written digits from 0 to 9. For more information on setting up the data used for training and validation, see Create Simple Deep Learning Neural Network for Classification.

You can also prune a network using structured pruning, which eliminates connections by removing entire filters from the network. Structured pruning in combination with quantization can improve the inference speed and reduce the memory footprint of a network. For an example of structured pruning, see Prune Image Classification Network Using Taylor Scores.

Load Pretrained Network and Data

Load the training and validation data. Train a convolutional neural network for the classification task.

[imdsTrain, imdsValidation] = loadDigitDataset;
net = trainDigitDataNetwork(imdsTrain, imdsValidation);
trueLabels = imdsValidation.Labels;
classes = categories(trueLabels);

Create a minibatchqueue object containing the validation data. Set executionEnvironment to auto to evaluate the network on a GPU, if one is available. By default, the minibatchqueue object converts each output to a gpuArray if a GPU is available. Using a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox).

executionEnvironment = "auto";
miniBatchSize = 128;
imdsValidation.ReadSize = miniBatchSize;
mbqValidation = minibatchqueue(imdsValidation,1,...
    'MiniBatchSize',miniBatchSize,...
    'MiniBatchFormat','SSCB',...
    'MiniBatchFcn',@preprocessMiniBatch,...
    'OutputEnvironment',executionEnvironment);

Neural Network Pruning

The goal of neural network pruning is to identify and remove unimportant connections to reduce the size of the network without affecting network accuracy. In the following figure, on the left, the network has connections that map each neuron to the neuron of the next layer. After pruning, the network has fewer connections than the original network.

A pruning algorithm assigns a score to each parameter in the network. The score ranks the importance of each connection in the network. You can use one of two pruning approaches to achieve a target sparsity:

• One-shot pruning - Remove a specified percentage of connections based on their score in one step. This method is prone to layer collapse when you specify a high sparsity value.

• Iterative pruning - Achieve the target sparsity in a series of iterative steps. You can use this method when evaluated scores are sensitive to network structure. Scores are reevaluated at every iteration, so using a series of steps allows the network to move toward sparsity incrementally.

This example uses the iterative pruning method to achieve a target sparsity.

Iterative Pruning

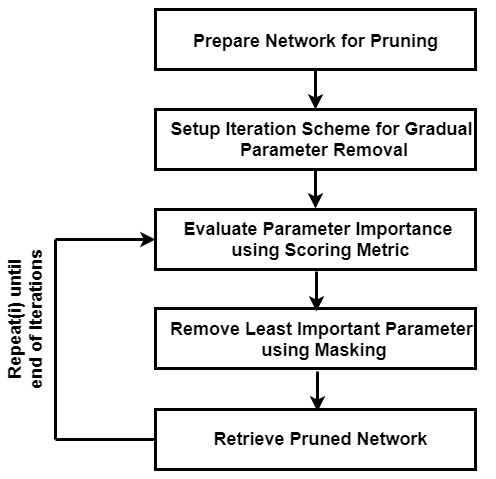
Convert to dlnetwork Object

In this example, you use the Synaptic Flow algorithm, which requires that you create a custom cost function and evaluate the gradients with respect to the cost function to calculate the parameter score. To create a custom cost function, first convert the pretrained network to a dlnetwork.

Convert the network to a layer graph and remove the layers used for classification using removeLayers.

lgraph = layerGraph(net.Layers);
lgraph = removeLayers(lgraph,["softmax","classoutput"]);
dlnet = dlnetwork(lgraph);

Use analyzeNetwork to analyze the network architecture and learnable parameters.

analyzeNetwork(dlnet)

Evaluate the accuracy of the network before pruning.

accuracyOriginalNet = evaluateAccuracy(dlnet,mbqValidation,classes,trueLabels)

accuracyOriginalNet = 0.9876

The layers with learnable parameters are the 3 convolutional layers and one fully connected layer. The network initially consists of total 21578 learnable parameters.

numTotalParams = sum(cellfun(@numel,dlnet.Learnables.Value))

numTotalParams = 21578

numNonZeroPerParam = cellfun(@(w)nnz(extractdata(w)),dlnet.Learnables.Value)

numNonZeroPerParam = 8×1

          72
           8
        1152
          16
        4608
          32
       15680
          10

Sparsity is defined as the percentage of parameters in the network with a value of zero. Check the sparsity of the network.

initialSparsity = 1-(sum(numNonZeroPerParam)/numTotalParams)

initialSparsity = 0

Before pruning, the network has a sparsity of zero.

Create Iteration Scheme

To define an iterative pruning scheme, specify the target sparsity and number of iterations. For this example, use linearly spaced iterations to achieve the target sparsity.

numIterations = 10; 
targetSparsity = 0.90;
iterationScheme = linspace(0,targetSparsity,numIterations); 

Pruning Loop

For each iteration, the custom pruning loop in this example performs the following steps:

• Calculate the score for each connection.

• Rank the scores for all connections in the network based on the selected pruning algorithm.

• Determine the threshold for removing connections with the lowest scores.

• Create the pruning mask using the threshold.

• Apply the pruning mask to learnable parameters of the network.

Network Mask

Instead of setting entries in the weight arrays directly to zero, the pruning algorithm creates a binary mask for each learnable parameter that specifies whether a connection is pruned. The mask allows you to explore the behavior of the pruned network and try different pruning schemes without changing the underlying network structure.

For example, consider the following weights.

testWeight = [10.4 5.6 0.8 9];

Create a binary mask for each parameter in testWeight.

testMask = [1 0 1 0];

Apply the mask to testWeight to get the pruned weights.

testWeightsPruned = testWeight.*testMask

testWeightsPruned = 1×4

   10.4000         0    0.8000         0

In iterative pruning, you create a binary mask for each iteration that contains pruning information. Applying the mask to the weights array does not change either the size of the array or the structure of the neural network. Therefore, the pruning step does not directly result in any speedup during inference or compression of the network size on disk.

Initialize a plot that compares the accuracy of the pruned network to the original network.

figure
plot(100*iterationScheme([1,end]),100*accuracyOriginalNet*[1 1],'*-b','LineWidth',2,"Color","b")
ylim([0 100])
xlim(100*iterationScheme([1,end]))
xlabel("Sparsity (%)")
ylabel("Accuracy (%)")
legend("Original Accuracy","Location","southwest")
title("Pruning Accuracy")    
grid on

Magnitude Pruning

Magnitude pruning [1] assigns a score to each parameter equal to its absolute value. It is assumed that the absolute value of a parameter corresponds to its relative importance to the accuracy of the trained network.

Initialize the mask. For the first iteration, you do not prune any parameters and the sparsity is 0%.

pruningMaskMagnitude = cell(1,numIterations); 
pruningMaskMagnitude{1} = dlupdate(@(p)true(size(p)), dlnet.Learnables);

Below is an implementation of magnitude pruning. The network is pruned to various target sparsities in a loop to provide the flexibility to choose a pruned network based on its accuracy.

lineAccuracyPruningMagnitude = animatedline('Color','g','Marker','o','LineWidth',1.5);
legend("Original Accuracy","Magnitude Pruning Accuracy","Location","southwest")

% Compute magnitude scores
scoresMagnitude = calculateMagnitudeScore(dlnet);

for idx = 1:numel(iterationScheme)

    prunedNetMagnitude = dlnet;
    
    % Update the pruning mask
    pruningMaskMagnitude{idx} = calculateMask(scoresMagnitude,iterationScheme(idx));
    
    % Check the number of zero entries in the pruning mask
    numPrunedParams = sum(cellfun(@(m)nnz(~extractdata(m)),pruningMaskMagnitude{idx}.Value));
    sparsity = numPrunedParams/numTotalParams;
    
    % Apply pruning mask to network parameters
    prunedNetMagnitude.Learnables = dlupdate(@(W,M)W.*M, prunedNetMagnitude.Learnables, pruningMaskMagnitude{idx});
    
    % Compute validation accuracy on pruned network
    accuracyMagnitude = evaluateAccuracy(prunedNetMagnitude,mbqValidation,classes,trueLabels);
    
    % Display the pruning progress
    addpoints(lineAccuracyPruningMagnitude,100*sparsity,100*accuracyMagnitude)
    drawnow
end

SynFlow Pruning

Synaptic flow conservation (SynFlow) [2] scores are used for pruning. You can use this method to prune networks that use linear activation functions such as ReLU.

Initialize the mask. For the first iteration, no parameters are pruned, and the sparsity is 0%.

pruningMaskSynFlow = cell(1,numIterations); 
pruningMaskSynFlow{1} = dlupdate(@(p)true(size(p)),dlnet.Learnables);

The input data you use to compute the scores is a single image containing ones. If you are using a GPU, convert the data to a gpuArray.

dlX = dlarray(ones(net.Layers(1).InputSize),'SSC');
if (executionEnvironment == "auto" && canUseGPU) || executionEnvironment == "gpu"
    dlX = gpuArray(dlX);
end

The below loop implements iterative synaptic flow score for pruning [2] where a custom cost function evaluates the SynFlow score for each parameter used for network pruning.

lineAccuracyPruningSynflow = animatedline('Color','r','Marker','o','LineWidth',1.5);
legend("Original Accuracy","Magnitude Pruning Accuracy","Synaptic Flow Accuracy","Location","southwest")

prunedNetSynFlow = dlnet;

% Iteratively increase sparsity
for idx = 1:numel(iterationScheme)
    % Compute SynFlow scores
    scoresSynFlow = calculateSynFlowScore(prunedNetSynFlow,dlX);
    
    % Update the pruning mask
    pruningMaskSynFlow{idx} = calculateMask(scoresSynFlow,iterationScheme(idx));
    
    % Check the number of zero entries in the pruning mask
    numPrunedParams = sum(cellfun(@(m)nnz(~extractdata(m)),pruningMaskSynFlow{idx}.Value));
    sparsity = numPrunedParams/numTotalParams;
    
    % Apply pruning mask to network parameters
    prunedNetSynFlow.Learnables = dlupdate(@(W,M)W.*M, prunedNetSynFlow.Learnables, pruningMaskSynFlow{idx});
    
    % Compute validation accuracy on pruned network
    accuracySynFlow = evaluateAccuracy(prunedNetSynFlow,mbqValidation,classes,trueLabels);
     
    % Display the pruning progress
    addpoints(lineAccuracyPruningSynflow,100*sparsity,100*accuracySynFlow)
    drawnow
end

Investigate Structure of Pruned Network

Choosing how much to prune a network is a trade-off between accuracy and sparsity. Use the sparsity versus accuracy plot to select the iteration with the desired sparsity level and acceptable accuracy.

pruningMethod = "SynFlow";
selectedIteration = 8;

prunedDLNet = createPrunedNet(dlnet,selectedIteration,pruningMaskSynFlow,pruningMaskMagnitude,pruningMethod);

[sparsityPerLayer,prunedChannelsPerLayer,numOutChannelsPerLayer,layerNames] = pruningStatistics(prunedDLNet);

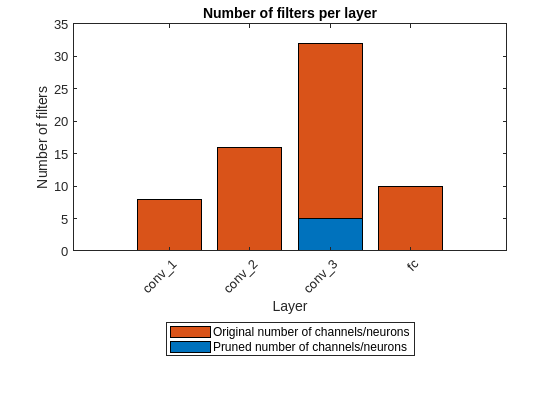
Earlier convolutional layers are typically pruned less since they contain more relevant information about the core low-level structure of the image (e.g. edges and corners) which are essential for interpreting the image.

Plot the sparsity per layer for the selected pruning method and iteration.

figure
bar(sparsityPerLayer*100)
title("Sparsity per layer")
xlabel("Layer")
ylabel("Sparsity (%)")
xticks(1:numel(sparsityPerLayer))
xticklabels(layerNames)
xtickangle(45)
set(gca,'TickLabelInterpreter','none')

The pruning algorithm prunes single connections when you specify a low target sparsity. When you specify a high target sparsity, the pruning algorithm can prune whole filters and neurons in convolutional or fully connected layers.

figure
bar([prunedChannelsPerLayer,numOutChannelsPerLayer-prunedChannelsPerLayer],"stacked")
xlabel("Layer")
ylabel("Number of filters")
title("Number of filters per layer")
xticks(1:(numel(layerNames)))
xticklabels(layerNames)
xtickangle(45)
legend("Pruned number of channels/neurons" , "Original number of channels/neurons","Location","southoutside")
set(gca,'TickLabelInterpreter','none')

Evaluate Network Accuracy

Compare the accuracy of the network before and after pruning.

YPredOriginal = modelPredictions(dlnet,mbqValidation,classes);
accOriginal = mean(YPredOriginal == trueLabels)

accOriginal = 0.9876

YPredPruned = modelPredictions(prunedDLNet,mbqValidation,classes);
accPruned = mean(YPredPruned == trueLabels)

accPruned = 0.9332

Create a confusion matrix chart to explore the true class labels to the predicted class labels for the original and pruned network.

figure
confusionchart(trueLabels,YPredOriginal);
title("Original Network")

The validation set of the digits data contains 250 images for each class, so if a network predicts the class of each image perfectly, all scores on the diagonal equal 250 and no values are outside of the diagonal.

confusionchart(trueLabels,YPredPruned);
title("Pruned Network")

When pruning a network, compare the confusion chart of the original network and the pruned network to check how the accuracy for each class label changes for the selected sparsity level. If all numbers on the diagonal decrease roughly equally, no bias is present. However, if the decreases are not equal, you might need to choose a pruned network from an earlier iteration by reducing the value of the variable selectedIteration.

Quantize Pruned Network

Deep neural networks trained in MATLAB use single-precision floating point data types. Even networks that are small require a considerable amount of memory and hardware to perform floating-point arithmetic operations. These restrictions can inhibit deployment of deep learning models that have low computational power and less memory resources. By using a lower precision to store the weights and activations, you can reduce the memory requirements of the network. You can use Deep Learning Toolbox in tandem with the Deep Learning Model Quantization Library support package to reduce the memory footprint of a deep neural network by quantizing the weights, biases, and activations of the convolution layers to 8-bit scaled integer data types.

Pruning a network impacts the range statistics of parameters and activations at each layer, so the accuracy of the quantized network can change. To explore this difference, quantize the pruned network and use the quantized network to perform inference.

Split the data into calibration and validation data sets.

calibrationDataStore = splitEachLabel(imdsTrain,0.1,'randomize');
validationDataStore = imdsValidation;

Create a dlquantizer object and specify the pruned network as the network to quantize.

prunedNet  = assembleNetwork([prunedDLNet.Layers ; net.Layers(end-1:end)]);

quantObjPrunedNetwork = dlquantizer(prunedNet,'ExecutionEnvironment','GPU'); 

Use the calibrate function to exercise the network with the calibration data and collect range statistics for the weights, biases, and activations at each layer.

calResults = calibrate(quantObjPrunedNetwork, calibrationDataStore)

calResults=21×5 table
        Optimized Layer Name        Network Layer Name    Learnables / Activations    MinValue     MaxValue
    ____________________________    __________________    ________________________    _________    ________

    {'conv_1_Weights'          }      {'conv_1'    }           "Weights"               -0.45091      1.1139
    {'conv_1_Bias'             }      {'conv_1'    }           "Bias"                 -0.029675    0.073755
    {'conv_2_Weights'          }      {'conv_2'    }           "Weights"               -0.50585       0.565
    {'conv_2_Bias'             }      {'conv_2'    }           "Bias"                 -0.080804     0.26643
    {'conv_3_Weights'          }      {'conv_3'    }           "Weights"               -0.42394      0.4668
    {'conv_3_Bias'             }      {'conv_3'    }           "Bias"                  -0.19857     0.20511
    {'fc_Weights'              }      {'fc'        }           "Weights"               -0.30973     0.29011
    {'fc_Bias'                 }      {'fc'        }           "Bias"                  -0.23231     0.16511
    {'imageinput'              }      {'imageinput'}           "Activations"                  0         255
    {'imageinput_normalization'}      {'imageinput'}           "Activations"                  0           1
    {'conv_1'                  }      {'conv_1'    }           "Activations"           -0.92647      7.3292
    {'relu_1'                  }      {'relu_1'    }           "Activations"                  0      7.3292
    {'maxpool_1'               }      {'maxpool_1' }           "Activations"                  0      7.3292
    {'conv_2'                  }      {'conv_2'    }           "Activations"            -8.6922      27.103
    {'relu_2'                  }      {'relu_2'    }           "Activations"                  0      27.103
    {'maxpool_2'               }      {'maxpool_2' }           "Activations"                  0      27.103
      ⋮

Use the validate function to compare the results of the network before and after quantization using the validation data set.

valResults = validate(quantObjPrunedNetwork, validationDataStore);

Examine the MetricResults.Result field of the validation output to see the accuracy of the quantized network.

valResults.MetricResults.Result

ans=2×2 table
    NetworkImplementation    MetricOutput
    _____________________    ____________

     {'Floating-Point'}         0.9332   
     {'Quantized'     }         0.9308   

Mini Batch Preprocessing Function

The preprocessMiniBatch function preprocesses a mini-batch of predictors by extracting the image data from the input cell array and concatenate into a numeric array. For grayscale input, concatenating the data over the fourth dimension adds a third dimension to each image to use as a singleton channel dimension.

function X = preprocessMiniBatch(XCell)
% Extract image data from cell and concatenate.
X = cat(4,XCell{:});
end

Model Accuracy Function

Evaluate the classification accuracy of the dlnetwork. Accuracy is the percentage of labels correctly classified by the network.

function accuracy = evaluateAccuracy(dlnet,mbqValidation,classes,trueLabels)
YPred = modelPredictions(dlnet,mbqValidation,classes);
accuracy = mean(YPred == trueLabels);
end

SynFlow Score Function

The calculateSynFlowScore function calculates Synaptic Flow (SynFlow) scores. Synaptic saliency [2] is described as the class of gradient-based scores defined by the product of gradient of loss multiplied by the parameter value:

$\mathrm{synFlowScore}=\frac{\mathit{d}\left(\mathrm{loss}\right)}{\mathit{d}\theta }$*$\theta$

The SynFlow score is a synaptic saliency score that uses the sum of all network outputs as a loss function:

$$\mathrm{loss}=\sum _{}^{}\mathit{f}\left(\mathrm{abs}\left(\theta \right),\mathit{X}\right)$$

$\mathit{f}$ is the function represented by the neural network

$\theta$ are the parameters of the network

$\mathit{X}$ is the input array to the network

To compute parameter gradients with respect to this loss function, use dlfeval and a model gradients function.

function score = calculateSynFlowScore(dlnet,dlX)
dlnet.Learnables = dlupdate(@abs, dlnet.Learnables);
gradients = dlfeval(@modelGradients,dlnet,dlX);
score = dlupdate(@(g,w)g.*w, gradients, dlnet.Learnables);
end

Model Gradients for SynFlow Score

function gradients = modelGradients(dlNet,inputArray)
% Evaluate the gradients on a given input to the dlnetwork
dlYPred = predict(dlNet,inputArray);
pseudoloss = sum(dlYPred,'all');
gradients = dlgradient(pseudoloss,dlNet.Learnables);
end

Magnitude Score Function

The calculateMagnitudeScore function returns the magnitude score, defined as the element-wise absolute value of the parameters.

function score = calculateMagnitudeScore(dlnet)
score = dlupdate(@abs, dlnet.Learnables);
end

Mask Generation Function

The calculateMask function returns a binary mask for the network parameters based on the given scores and the target sparsity.

function mask = calculateMask(scoresMagnitude,sparsity)
% Compute a binary mask based on the parameter-wise scores such that the mask contains a percentage of zeros as specified by sparsity.

% Flatten the cell array of scores into one long score vector
flattenedScores = cell2mat(cellfun(@(S)extractdata(gather(S(:))),scoresMagnitude.Value,'UniformOutput',false));
% Rank the scores and determine the threshold for removing connections for the
% given sparsity
flattenedScores = sort(flattenedScores);
k = round(sparsity*numel(flattenedScores));
if k==0
    thresh = 0;
else
    thresh = flattenedScores(k);
end
% Create a binary mask 
mask = dlupdate( @(S)S>thresh, scoresMagnitude);
end

Model Predictions Function

The modelPredictions function takes as input a dlnetwork object dlnet, a minibatchqueue of input data mbq, and the network classes, and computes the model predictions by iterating over all data in the minibatchqueue object. The function uses the onehotdecode function to find the predicted class with the highest score.

function predictions = modelPredictions(dlnet,mbq,classes)
predictions = [];
while hasdata(mbq)
    dlXTest = next(mbq);
    dlYPred = softmax(predict(dlnet,dlXTest));
    YPred = onehotdecode(dlYPred,classes,1)';
    predictions = [predictions; YPred];
end
reset(mbq)
end

Apply Pruning Function

The createPrunedNet function returns the pruned dlnetwork for the specified pruning algorithm and iteration.

function prunedNet = createPrunedNet(dlnet,selectedIteration,pruningMaskSynFlow,pruningMaskMagnitude,pruningMethod)
switch pruningMethod
    case "Magnitude"
        prunedNet = dlupdate(@(W,M)W.*M, dlnet, pruningMaskMagnitude{selectedIteration});
    case "SynFlow"
        prunedNet = dlupdate(@(W,M)W.*M, dlnet, pruningMaskSynFlow{selectedIteration});
end
end

Pruning Statistics Function

The pruningStatistics function extracts detailed layer-level pruning statistics such as the layer-level sparsity and the number of filters or neurons being pruned.

sparsityPerLayer - percentage of parameters pruned in each layer

prunedChannelsPerLayer - number of channels/neurons in each layer that can be removed as a result of pruning

numOutChannelsPerLayer - number of channels/neurons in each layer

function [sparsityPerLayer,prunedChannelsPerLayer,numOutChannelsPerLayer,layerNames] = pruningStatistics(dlnet)

layerNames = unique(dlnet.Learnables.Layer,'stable');
numLayers = numel(layerNames);
layerIDs = zeros(numLayers,1);
for idx = 1:numel(layerNames)
    layerIDs(idx) = find(layerNames(idx)=={dlnet.Layers.Name});
end

sparsityPerLayer = zeros(numLayers,1);
prunedChannelsPerLayer = zeros(numLayers,1);
numOutChannelsPerLayer = zeros(numLayers,1);

numParams = zeros(numLayers,1);
numPrunedParams = zeros(numLayers,1);
for idx = 1:numLayers
    layer = dlnet.Layers(layerIDs(idx));
    
    % Calculate the sparsity
    paramIDs = strcmp(dlnet.Learnables.Layer,layerNames(idx));
    paramValue = dlnet.Learnables.Value(paramIDs);
    for p = 1:numel(paramValue)
        numParams(idx) = numParams(idx) + numel(paramValue{p});
        numPrunedParams(idx) = numPrunedParams(idx) + nnz(extractdata(paramValue{p})==0);
    end

    % Calculate channel statistics
    sparsityPerLayer(idx) = numPrunedParams(idx)/numParams(idx);
    switch class(layer)
        case "nnet.cnn.layer.FullyConnectedLayer"
            numOutChannelsPerLayer(idx) = layer.OutputSize;
            prunedChannelsPerLayer(idx) = nnz(all(layer.Weights==0,2)&layer.Bias(:)==0);
        case "nnet.cnn.layer.Convolution2DLayer"
            numOutChannelsPerLayer(idx) = layer.NumFilters;
            prunedChannelsPerLayer(idx) = nnz(reshape(all(layer.Weights==0,[1,2,3]),[],1)&layer.Bias(:)==0);
        case "nnet.cnn.layer.GroupedConvolution2DLayer"
            numOutChannelsPerLayer(idx) = layer.NumGroups*layer.NumFiltersPerGroup;
            prunedChannelsPerLayer(idx) = nnz(reshape(all(layer.Weights==0,[1,2,3]),[],1)&layer.Bias(:)==0);
        otherwise
            error("Unknown layer: "+class(layer))
    end
end
end

Load Digits Data set Function

The loadDigitDataset function loads the Digits data set and splits the data into training and validation data.

function [imdsTrain, imdsValidation] = loadDigitDataset()
digitDatasetPath = fullfile(matlabroot,'toolbox','nnet','nndemos', ...
    'nndatasets','DigitDataset');
imds = imageDatastore(digitDatasetPath, ...
    'IncludeSubfolders',true,'LabelSource','foldernames');
[imdsTrain, imdsValidation] = splitEachLabel(imds,0.75,"randomized");
end

Train Digit Recognition Network Function

The trainDigitDataNetwork function trains a convolutional neural network to classify digits in grayscale images.

function net = trainDigitDataNetwork(imdsTrain,imdsValidation)
layers = [
    imageInputLayer([28 28 1],"Normalization","rescale-zero-one")
    convolution2dLayer(3,8,'Padding','same')
    reluLayer
    maxPooling2dLayer(2,'Stride',2)
    
    convolution2dLayer(3,16,'Padding','same')
    reluLayer
    maxPooling2dLayer(2,'Stride',2)
    
    convolution2dLayer(3,32,'Padding','same')
    reluLayer
    
    fullyConnectedLayer(10)
    softmaxLayer
    classificationLayer];

% Specify the training options
options = trainingOptions('sgdm', ...
    'InitialLearnRate',0.01, ...
    'MaxEpochs',10, ...
    'Shuffle','every-epoch', ...
    'ValidationData',imdsValidation, ...
    'ValidationFrequency',30, ...
    'Verbose',false, ...
    'Plots','none',"ExecutionEnvironment","auto");

% Train network
net = trainNetwork(imdsTrain,layers,options);
end

References

[1] Song Han, Jeff Pool, John Tran, and William J. Dally. 2015. "Learning Both Weights and Connections for Efficient Neural Networks." Advances in Neural Information Processing Systems 28 (NIPS 2015): 1135–1143.

[2] Hidenori Tanaka, Daniel Kunin, Daniel L. K. Yamins, and Surya Ganguli 2020. "Pruning Neural Networks Without Any Data by Iteratively Conserving Synaptic Flow." 34th Conference on Neural Information Processing Systems (NeurlPS 2020)