Lowess Smoothing
About Lowess Smoothing
Use Lowess models to fit smooth surfaces to your data. The names “lowess” and “loess” are derived from the term “locally weighted scatter plot smooth,” as both methods use locally weighted linear regression to smooth data. The process is weighted because the toolbox defines a regression weight function for the data points contained within the span. In addition to the regression weight function, the Robust option is a weight function that can make the process resistant to outliers.
For more information on these two types of smoothing fit, see Local Regression Smoothing.
Select Lowess Fit Interactively
Open the Curve Fitter app by entering curveFitter at the
MATLAB® command line. Alternatively, on the Apps tab, in the Math, Statistics and
Optimization group, click Curve Fitter.
On the Curve Fitter tab, in the Fit Type section, select a Lowess fit. The app uses locally weighted linear regression to smooth the data.
In the Fit Options pane, you can try different fit options.
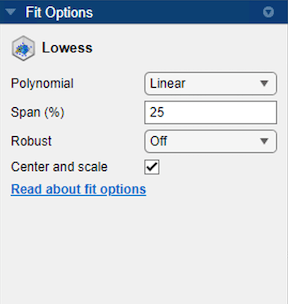
You can set the regression Polynomial model to
LinearorQuadratic.You can use Span to set the span as a percentage of the total number of data points in the data set. The app uses neighboring data points defined within the span to determine each smoothed value. This smoothing process is called “local.”
Tip
Increase the span to make the surface smoother. Reduce the span to make the surface follow the data more closely.
You can set the Robust linear least-squares fitting method to
Off,LAR, orBisquare. The local regression uses the Robust option. Using the Robust weight function can make the smoothing resistant to outliers. For details, see theRobustname-value argument of thefitoptionsfunction.
Tip
If your data variables have very different scales, select and clear the Center and scale check box to see the difference in the fit. Normalizing the variables can strongly influence the results of a lowess fit.
For an example on how to create a lowess fit interactively, see Surface Fitting to Franke Data.
Fit Lowess Models Using the fit Function
This example shows how to use the fit function to fit a Lowess model to data.
Load some data and fit a Lowess model by specifying 'lowess' when calling the fit function.
load franke f = fit([x y],z,'lowess')
f =
Locally weighted smoothing linear regression:
f(x,y) = lowess (linear) smoothing regression computed from p
Coefficients:
p = coefficient structure
plot(f,[x y],z)

For a command-line example fitting a Lowess model, see Fit Smooth Surfaces to Investigate Fuel Efficiency.