sumblk
Summing junction for name-based interconnections
Description
S = sumblk(formula)formula in the form of a transfer
function (tf) model, S. The string
formula specifies an equation that relates the scalar input and
output signals of S, such as "e = r - y". The
function sets the InputName and OutputName properties
of S based on formula. Use S in
conjunction with connect to interconnect dynamic system
models and derive aggregate models for block diagrams.
S = sumblk(formula,signalsize)signalsize elements. sumblk sets the
InputName and OutputName properties by vector
expansion of the signal names in formula.
S = sumblk(formula,signames1,...,signamesN)formula by the signal names
signames. Indicate a placeholder in formula by
using a signal name beginning with %. The number of
signames arguments must match the number of placeholders in
formula. The first placeholder in formula is
replaced by signames1, the second by signames2,
and so on.
Examples
Create the summing junction of the following illustration. All signals are scalar-valued.
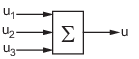
This summing junction has the formula u = u1 + u2 + u3. Use this formula with sumblk to create the summing junction.
S = sumblk('u = u1 + u2 + u3');S is the transfer function (tf) representation of the sum u = u1 + u2 + u3. That is, S is a static-gain tf with three inputs and one output, which is equal to the sum of the inputs. The transfer function S gets its input and output names from the formula.
S.OutputName
ans = 1×1 cell array
{'u'}
S.InputName
ans = 3×1 cell
{'u1'}
{'u2'}
{'u3'}
Therefore, you can use S with the name-based syntax of the connect command to build aggregate models such as the system of the following block diagram.
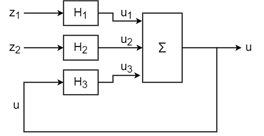
To do so, create LTI models for H1, H2, and H3, and name their inputs and outputs according to the diagram. For this example, use transfer functions.
H1 = tf(1,[1 2],"InputName","z1","OutputName","u1"); H2 = tf([1 -2],[1 1],"InputName","z2","OutputName","u2"); H3 = tf(2,[2 1],"InputName","u","OutputName","u3");
Connect the models and the summing junction to create an aggregate model with inputs z1 and z2 and output u. The connect command automatically connects the outputs of the components to inputs with matching names.
T = connect(H1,H2,H3,S,{"z1","z2"},{"u"});
T.InputNameans = 2×1 cell
{'z1'}
{'z2'}
T.OutputName
ans = 1×1 cell array
{'u'}
Create the summing junction v = u - d where u, d, v are vector-valued signals of length 2. This summing junction is shown in the following diagram, where each arrow represents two signals.

This summing junction outputs v(1) = u(1) - d(1) and v(2) = u(2) - d(2). To create this junction using sumblk, specify both the formula and the signal length.
S = sumblk('v = u - d',2);
size(S)Transfer function with 2 outputs and 4 inputs.
The result is a transfer function with four inputs and two outputs: two inputs each for d and u, and two outputs for v. sumblk automatically performs vector expansion of the signal names and assigns them to S.InputName and S.OutputName.
S.InputName
ans = 4×1 cell
{'u(1)'}
{'u(2)'}
{'d(1)'}
{'d(2)'}
S.OutputName
ans = 2×1 cell
{'v(1)'}
{'v(2)'}
You can connect S to other dynamic system models to build aggregate models, as you would use any other MIMO transfer function. For instance, suppose that you want to create a model representing the following two-channel feedback loop, that is, a feedback loop in which each line in the diagram represents two signals.
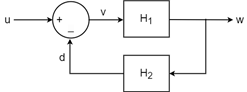
Create two-input, two-output models for H1 and H2, and set their InputName and OutputName properties as indicated by the diagram. For this example, use random state-space models.
H1 = rss(3,2,2); H1.InputName = 'v'; H1.OutputName = 'w'; H2 = rss(3,2,2); H2.InputName = 'w'; H2.OutputName = 'd';
Note that the signal names in the dynamic system models are automatically expanded, just as sumblk expands the signal names of S. For instance, examine the outputs of H1.
H1.OutputName
ans = 2×1 cell
{'w(1)'}
{'w(2)'}
The connect command also performs this expansion. Thus, you can assemble the aggregate system with the following command.
T = connect(S,H1,H2,'u','w'); size(T)
State-space model with 2 outputs, 2 inputs, and 6 states.
As shown in the example Summing Junction with Vector-Valued Signals, when you create a summing junction for vector signals, by default sumblk appends an index to the signal names that you provide. If you need to specify distinct signal names instead of this vector expansion, use a placeholder in the summing-junction formula to represent the signals you want to name. Then, use the signames input argument to provide the specific names to substitute for the placeholder in creating the summing junction.
For instance, create a summing junction having the following formula.
This formula is the summing junction shown in the following diagram, where setpoint represents two inputs and e represents two outputs.

To create this summing junction, allow sumblk to expand e and setpoint, but use a signal name beginning with % as a placeholder for the specific signal names you provide in the signames argument.
formula = 'e = setpoint - %y'; signames = ["alpha","q"]; S = sumblk(formula,signames);
sumblk replaces the placeholder %y with the signal names alpha and q and expands the other signal names. Note that sumblk takes the size of the vector signals from the number of signals in signames. Thus, the setpoint input and e output of S each contain two signals.
S.InputName
ans = 4×1 cell
{'setpoint(1)'}
{'setpoint(2)'}
{'alpha' }
{'q' }
S.OutputName
ans = 2×1 cell
{'e(1)'}
{'e(2)'}
This syntax is particularly useful when you want to create a summing junction to connect existing models whose InputName or OutputName properties are already set. For instance, consider the following two-input, two-output state-space model.
A = [-0.004 0.03; 0.03 -0.19];
B = [0.3 0.2; -0.06 0];
C = [0.99 0.5; 0 0];
D = 0;
G = ss(A,B,C,D);
G.InputName = {'angle','rate'};
G.OutputName = {'current','temp'};Create a summing junction that subtracts the outputs of G from a pair of reference inputs, such that
To do so, use a placeholder for these signals in the formula. Then, use G.OutputName as the signames input.
S = sumblk('e = ref - %outputs',G.OutputName);
S.InputNameans = 4×1 cell
{'ref(1)' }
{'ref(2)' }
{'current'}
{'temp' }
You can use multiple placeholders to replace multiple elements of the formula. sumblk replaces the placeholders in the order you provide them. For instance, give the reference signals specific names instead of ref(1) and ref(2).
refnames = ["refcur","reftemp"]; S = sumblk('e = %refs - %outputs',refnames,G.OutputName); S.InputName
ans = 4×1 cell
{'refcur' }
{'reftemp'}
{'current'}
{'temp' }
Input Arguments
Equation that relates the input and output signals of the summing junction transfer
function S, specified as a string or character vector. For example,
consider the summing junction of the following diagram.

To represent this summing junction as a three-input, one-output transfer function, use the following commands.
formula = "e = r + d - y"; S = sumblk(formula);
For vector-valued signals, you can optionally use one or more placeholders in
formula to control the names that sumblk
assigns to S.InputName and S.OutputName. To put a
placeholder in formula, use a signal name that begins with
%. When assigning signal names to S, the
sumblk command replaces each placeholder with the names you
provide in the signames argument.
Such placeholders are particularly useful for creating summing junctions for
connecting existing models that have named signals. For example, if C
and G are dynamic system models with nonempty
InputName and OutputName properties,
respectively, you can create a summing junction using the following expression.
S = sumblk("%e = r - %y",C.InputName,G.OutputName)sumblk uses the values of C.InputName and
G.OutputName in place of %e and
%y, respectively. The vector dimension of
C.InputName and G.OutputName must match.
sumblk assigns the signal r the same dimension.
For an example, see Specify Individual Names in Summing Junction with Vector-Valued Signals.
Number of elements in each input and output signal of S,
specified as a positive integer. Setting signalsize greater than 1
lets you specify a summing junction that operates on vector-valued signals. For
instance, S = sumblk("e = r - y",2) creates a summing junction where
each of the inputs r and y and the output
e is a vector signal with two elements. See Summing Junction with Vector-Valued Signals.
Substitute signal names for a placeholder (signal name beginning with
%) in the argument formula, specified as a
string array or a cell array of character vectors. Provide one
signames argument for each placeholder in
formula.
Specify signames as:
A string array, such as
["alpha","q"].A cell array of signal names, such as
{'alpha','q'}.The
InputNameorOutputNameproperty of a model in the MATLAB® workspace. For example:S = sumblk("%e = r - y",C.InputName)This command creates a summing junction whose outputs have the same name as the inputs of the model
Cin the MATLAB workspace. For an example showing how to usesignames, see Specify Individual Names in Summing Junction with Vector-Valued Signals.If you use placeholders and the
signamesargument, thensumblksets the vector length of the signals ofS. If you use multiple placeholders, then allsignamesarguments must have the same number of signals.
Output Arguments
Transfer function for the summing junction, returned as a tf model.
sumblk sets the InputName and
OutputName properties of S using the signal
names in formula. For instance, if you enter S = sumblk("e
= r + d - y"), then sumblk creates
S with S.InputName = {'r';'d';'y'} and
S.OutputName = {'e'}. Use these input and output names to
interconnect S with other dynamic system models to build composite
systems. For an example, see Summing Junction with Scalar-Valued Signals.
If signalsize is greater than 1, then S has
signalsize inputs (or outputs) per signal name in
formula. The function sets S.InputName and
S.OutputName by applying vector expansion to the signal name
specified in formula, such as
{'e(1)','e(2)',...}. For an example, see Summing Junction with Vector-Valued Signals.
If you use placeholders in formula, then
sumblk sets the InputName and
OutputName properties of S using the names you
provide in signames. For an example, see Specify Individual Names in Summing Junction with Vector-Valued Signals.
Version History
Introduced in R2008a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)