xelim
Description
rsys = xelim(sys,elim)sys by eliminating the states
specified in the vector elim. The full state vector
x is partitioned as x =
[x1;x2]
where x1 is the reduced state vector and
x2 is eliminated.
This function is useful to eliminate states known to settle quickly (fast modes) or
contribute little to the input/output map. When you don’t know which states to eliminate,
use reducespec and
the model-order reduction workflow.
Examples
Consider the following continuous fourth-order model.
To reduce its order, first compute a balanced state-space realization with balreal.
h = tf([1 11 36 26],[1 14.6 74.96 153.7 99.65]); [hb,g] = balreal(h);
Examine the Gramians.
g'
ans = 1×4
0.1394 0.0095 0.0006 0.0000
The last three diagonal entries of the balanced Gramians are relatively small. Eliminate these three least-contributing states with xelim, using both matched DC gain and direct-deletion methods.
hmdc = xelim(hb,2:4,"MatchDC"); hdel = xelim(hb,2:4,"Truncate");
Both hmdc and hdel are first-order models. Compare their Bode responses against that of the original model.
bp = bodeplot(h,hmdc,'r--',hdel,'k-.'); bp.PhaseMatchingEnabled = 'on'; legend("Original","State elimination (match DC)",... "State elimination (truncate)");
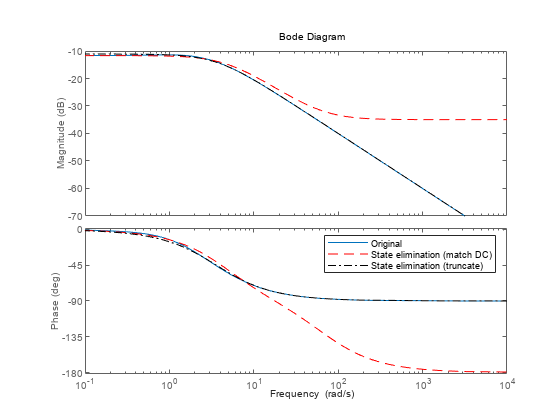
The reduced-order model hdel is clearly a better frequency-domain approximation of h. Now compare the step responses.
stepplot(h,hmdc,'r--',hdel,'k-.') legend("Original","State elimination (match DC)",... "State elimination (truncate)",Location="southeast");

While hdel accurately reflects the transient behavior, only hmdc gives the true steady-state response.
For faster and more accurate results, use reducespec for model reduction workflows.
Since R2024a
This example shows how to use findop to find the matching initial condition for a reduced model obtained with xelim.
Create a random state-space model.
rng(0) sys = rss(10,1,2);
To reduce its order, first compute a balanced state-space realization with balreal.
[sysb,g] = balreal(sys); g'
ans = 1×10
13.2301 4.9468 1.0334 0.4597 0.0644 0.0287 0.0057 0.0007 0.0000 0.0000
Based on the small Gramians, you can eliminate last 6 states from balanced realization sysb.
rsys = xelim(sysb,5:10,"MatchDC");With MatchDC option, the reduced model states may differ from because xelim scales and sometimes transforms the states to obtain the reduced model. Therefore, the initial conditions of the original model and reduced model may be different.
Compute the initial condition of the original and reduced models.
op = findop(sysb,u=[1 -1]); opr = findop(rsys,u=[1 -1]); op.x(1:4)
ans = 4×1
18.9852
-3.2735
1.6693
0.5918
opr.x
ans = 4×1
18.9852
-3.2735
0.8347
0.5918
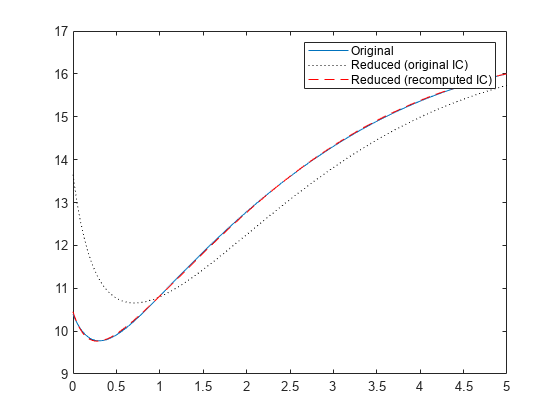
The initial states for both models are different. Therefore, it is recommended to recompute the operating condition when reducing models. Using operating conditions of the original model with the reduced model may result in incorrect responses. For example, compare the initial response of the reduced model with the operating condition from the original model.
t = 0:0.01:5; y = initial(sysb,op.x,t); y1 = initial(rsys,op.x(1:4),t); y2 = initial(rsys,opr.x,t); plot(t,y,t,y1,'k:',t,y2,'r--') legend("Original","Reduced (original IC)", "Reduced (recomputed IC)");
Input Arguments
Dynamic system model, specified as an ordinary or sparse LTI model.
The input model must have a valid state-space representation, such as
tf, ss, sparss,
mechss models. For generalized or uncertain state-space models
(genss, uss), the function uses the current value of
the model. For identified models (idss), the function uses the
identified value.
State elimination vector, specified as one of these.
A vector containing index values of states you want to discard.
A vector of logical values of the same size as the number of states, where the
true(1) values specifies the states you want to discard.
State elimination method, specified as "MatchDC" or
"Truncate". This argument specifies how the function eliminates the
states with weak contribution.
"MatchDC"— Enforce matching DC gains. To do so, the algorithm treats x2 as infinitely fast and sets its derivative to zero. The resulting algebraic equation is used to express x2 in terms of x1 and eliminate it. For details, see Algorithms"Truncate"— Simply drop x2, and use x1 as reduced state.
The "Truncate" option tends to produce a better approximation in
the frequency domain, but the DC gains are not guaranteed to match.
Output Arguments
Reduced-order model, returned as a state-space model.
Algorithms
For a state-space model
the function partitions the state vector into x1 (to keep) and x2 (to eliminate).
For continuous-time models, this method sets the derivative of x2 to zero and solves the resulting equation for x1. The reduced-order model is given by
Similarly, for discrete-time models, the algorithm sets to recompute the matrices.
These equations of the algorithm describe only the general idea. The function performs
additional scaling and eliminates only a portion of
x2 when
A22 or
A22 –
E22 is nearly singular. This alters
x1 and the original initial condition
x1(0) is not valid. You can use the findop
function to compute matching initial conditions for the reduced model. For an example, see
Find Matching Initial Condition for Reduced Model.
For this method, the algorithm simply drops x2, and uses x1 as reduced state. The reduced-order model is given by
xelim returns a scaled version of this realization.
Version History
Introduced in R2023b
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)