Main Content

AI for Digital Predistortion Design

Since R2024a

To offset the effects of nonlinearities in a power amplifier (PA), you can use a neural network to apply digital predistortion (DPD) to the input signal.

Nonlinear behavior in PAs results in severe signal distortions and causes challenges for error-free reception of the high-frequency and high-bandwidth signals commonly transmitted in 5G NR [1]. DPD of the transmitted signal is a technique that you can use to compensate for PA nonlinearities that distort the signal. Typically, the PA nonlinear behavior is characterized in advance and DPD applies an inverse predistortion using some form of memory polynomials [2]. For an example, see Digital Predistortion to Compensate for Power Amplifier Nonlinearities. Experimentation with neural network-based DPD techniques shows promising results that offer better performance than the traditional memory polynomial DPD [1], [3], [4].

NN-DPD Structure

To use the neural-network-based DPD technique (NN-DPD), you can design an augmented real-valued time-delay neural network (ARVTDNN) as described in [4]. ARVTDNN has multiple fully connected layers and an augmented input.

This example uses the memory polynomial model commonly applied in the behavioral modeling and predistortion of PAs with memory effects. This equation shows the PA memory polynomial.

x(n)=f(u(n))=∑m=0M−1∑k=0K−1cmu(n−m)|u(n−m)|k

The output is a function of the delayed versions of the input signal, u(n), and also powers of the amplitudes of u(n) and its delayed versions.

You can input u(n) to the neural network and approximate function f(u(n)) as long as the neural network has enough layers and neurons per layer. The neural network can input u(n-m) and ∣u(n-m)k| to decrease the required complexity.

This figure shows the NN-DPD and its multiple fully connected layers. The input layer inputs the in-phase (Iin) and quadrature components (Qin) of the complex baseband samples. The Iin and Qin samples and m delayed versions are used as part of the input to account for the memory in the PA model. Additionally, to account for the nonlinearity of the PA, the amplitudes of the Iin and Qin samples up to the kth power are provided as inputs.

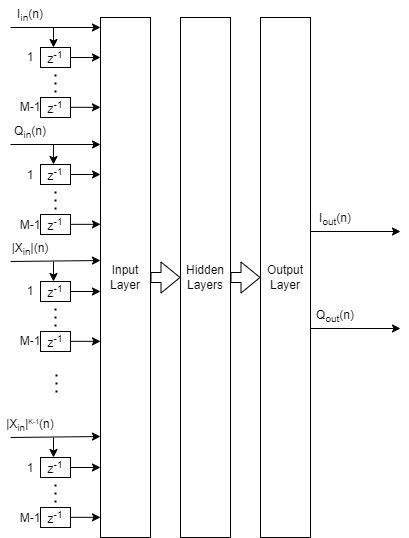
Neural network layers for DPD

During training,

  • Iin = ℜ(x(n))

  • Qin = ℑ(x(n))

  • Iout = ℜ(u(n))

  • Qout = ℑ(u(n))

while during deployment (inference),

  • Iin = ℜ(u(n))

  • Qin = ℑ(u(n))

  • Iout = ℜ(y(n))

  • Qout = ℑ(y(n))

ℜ and ℑ are the real and imaginary part operators, respectively.

End-to-End Workflow

These examples demonstrate workflows for training and deploying a neural network-based DPD design.

References

[1] Tarver, Chance, Liwen Jiang, Aryan Sefidi, and Joseph R. Cavallaro. “Neural Network DPD via Backpropagation through a Neural Network Model of the PA.” In 2019 53rd Asilomar Conference on Signals, Systems, and Computers, 358–62. Pacific Grove, CA, USA: IEEE, 2019. https://doi.org/10.1109/IEEECONF44664.2019.9048910.

[2] Morgan, Dennis R., Zhengxiang Ma, Jaehyeong Kim, Michael G. Zierdt, and John Pastalan. “A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers.” IEEE Transactions on Signal Processing 54, no. 10 (October 2006): 3852–60. https://doi.org/10.1109/TSP.2006.879264.

[3] Wu, Yibo, Ulf Gustavsson, Alexandre Graell i Amat, and Henk Wymeersch. “Residual Neural Networks for Digital Predistortion.” In GLOBECOM 2020 - 2020 IEEE Global Communications Conference, 01–06. Taipei, Taiwan: IEEE, 2020. https://doi.org/10.1109/GLOBECOM42002.2020.9322327.

[4] Wang, Dongming, Mohsin Aziz, Mohamed Helaoui, and Fadhel M. Ghannouchi. “Augmented Real-Valued Time-Delay Neural Network for Compensation of Distortions and Impairments in Wireless Transmitters.” IEEE Transactions on Neural Networks and Learning Systems 30, no. 1 (January 2019): 242–54. https://doi.org/10.1109/TNNLS.2018.2838039.

[5] Sun, Jinlong, Juan Wang, Liang Guo, Jie Yang, and Guan Gui. “Adaptive Deep Learning Aided Digital Predistorter Considering Dynamic Envelope.” IEEE Transactions on Vehicular Technology 69, no. 4 (April 2020): 4487–91. https://doi.org/10.1109/TVT.2020.2974506.

[6] Sun, Jinlong, Wenjuan Shi, Zhutian Yang, Jie Yang, and Guan Gui. “Behavioral Modeling and Linearization of Wideband RF Power Amplifiers Using BiLSTM Networks for 5G Wireless Systems.” IEEE Transactions on Vehicular Technology 68, no. 11 (November 2019): 10348–56. https://doi.org/10.1109/TVT.2019.2925562.

[7] Paaso, Henna, and Aarne Mammela. “Comparison of Direct Learning and Indirect Learning Predistortion Architectures.” In 2008 IEEE International Symposium on Wireless Communication Systems, 309–13. Reykjavik: IEEE, 2008. https://doi.org/10.1109/ISWCS.2008.4726067.