General CRC Syndrome Detector
Detect errors in received codeword frames according to generator polynomial
Libraries:
Communications Toolbox /
Error Detection and Correction /
CRC
Description
The General CRC Syndrome Detector block computes cyclic redundancy check (CRC) checksums for received codeword frames. For successful CRC detection in a communications system link, you must align the parameter settings of the General CRC Syndrome Detector block with the paired General CRC Generator block.
For more information, see CRC Syndrome Detector Operation.
Examples
Use a CRC code to detect frame errors in a noisy BPSK signal.
In the cm_ex_crc_noisy_bpsk_frames model, the CRC generator and detector pair use a standard CRC-4 polynomial, 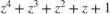 . The length of the CRC is 4 bits as determined by the degree of the polynomial. The number of checksums per frame is 1, so the full transmission frame has one CRC appended at the end.
. The length of the CRC is 4 bits as determined by the degree of the polynomial. The number of checksums per frame is 1, so the full transmission frame has one CRC appended at the end.
A binary signal frame gets a CRC code appended to the end of the frame. BPSK modulation is applied to the signal and the signal passes through an AWGN channel. The signal is demodulated, and then a CRC syndrome detector removes the CRC and calculates the CRC errors.
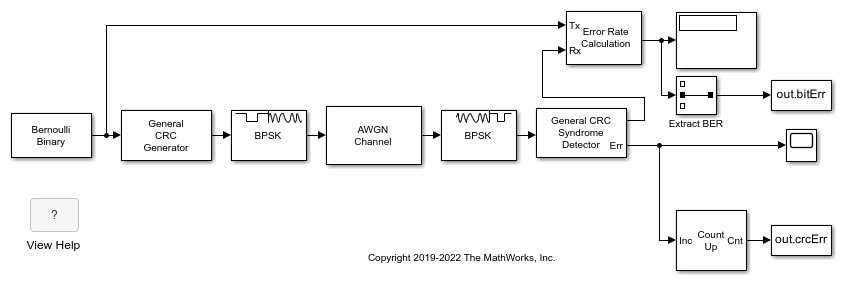
Generate 12-bit frames of binary data and append CRC bits. Based on the degree of the polynomial, 4 bits are appended to each frame. Apply BPSK modulation and pass the signal through an AWGN channel. Demodulate and use the CRC detector to determine if the frame is in error.
The results of the CRC detection are compared to a BER calculation.
Number of bit errors detected: 6 Number of crc errors detected: 7
Ports
Input
Received codeword, specified as a binary column vector.
Data Types: double | Boolean
Output
Output frame, returned as a binary column vector that inherits the data type of the input signal. The output frame contains the received codeword with the checksums removed.
The length of the output frame is n - k * r bits, where n is the size of the received codeword, k is the number of checksums per frame, and r is the degree of the generator polynomial.
Checksum error signal, returned as a binary column vector that
inherits the data type of the input signal. The length of
Err equals the value of Checksums per
frame. For each checksum computation, an element value of
0 in Err indicates no checksum error, and an
element value of 1 in Err indicates a checksum
error.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Generator polynomial for the CRC algorithm, specified as one of the following:
A polynomial character vector such as
'z^3 + z^2 + 1'.A binary row vector that represents the coefficients of the generator polynomial in order of descending power. The length of this vector is (N+1), where N is the degree of the generator polynomial. For example,
[1 1 0 1]represents the polynomial x3+ z2+ 1.An integer row vector containing the exponents of z for the nonzero terms in the polynomial in descending order. For example,
[3 2 0]represents the polynomial z3 + z2 + 1.
For more information, see Representation of Polynomials in Communications Toolbox.
The default value is the CRC-16-CCITT generator polynomial. This table lists some commonly used generator polynomials.
| CRC Name | Generator Polynomial |
|---|---|
| CRC-32 | 'z^32 + z^26 + z^23 + z^22 + z^16 + z^12 + z^11 + z^10 + z^8 +
z^7 + z^5 + z^4 + z^2 + z + 1' |
| CRC-24 | 'z^24 + z^23 + z^14 + z^12 + z^8 + 1' |
| CRC-16 | 'z^16 + z^15 + z^2 + 1' |
| CRC-16-CCITT | 'z^16 + z^12 + z^5 + 1' |
| Reversed CRC-16 | 'z^16 + z^14 + z + 1' |
| CRC-8 | 'z^8 + z^7 + z^6 + z^4 + z^2 + 1' |
| CRC-4 | 'z^4 + z^3 + z^2 + z + 1' |
Example: 'z^7 + z^2 + 1', [1 0 0 0 0 1 0
1], and [7 2 0] represent the same
polynomial, p(z) =
z
7 + z
2 + 1.
Initial states of the internal shift register, specified as a binary scalar or a binary row vector with a length equal to the degree of the generator polynomial. A scalar value is expanded to a row vector of equal length to the degree of the generator polynomial.
Select to use the direct algorithm for CRC checksum calculations. When cleared, the block uses the non-direct algorithm for CRC checksum calculations.
For more information on direct and non-direct algorithms, see Error Detection and Correction.
Select to flip the received codeword on a bytewise basis before entering
the data into the shift register. When Reflect input
bytes is selected, the received codeword length divided by
the value of the Checksums per frame
parameter must be an integer and a multiple of 8. When
Reflect input bytes is cleared, the block does not
flip the input data.
Select Reflect checksums before final XOR to flip the CRC checksums around their centers after the input data are completely through the shift register. When Reflect checksums before final XOR is cleared, the block does not flip the CRC checksums.
Final XOR, specified as a binary scalar or a binary row vector with a
length equal to the degree of the generator polynomial. The XOR operation
runs using the value of the Final XOR parameter and the
CRC checksum before comparing with the input checksum. A scalar value is
expanded to a row vector of equal length to the degree of the generator
polynomial. A setting of 0 is equivalent to no XOR
operation.
Number of checksums calculated for each frame, specified as a positive integer.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
The General CRC Syndrome Detector block supports detection of CRC checksum by using the indirect or direct CRC algorithm.
Indirect CRC Algorithm
The indirect CRC algorithm accepts a binary data vector, corresponding to a polynomial M, and appends a checksum of r bits, corresponding to a polynomial C. The concatenation of the input vector and the checksum then corresponds to the polynomial T = M×xr + C, since multiplying by xr corresponds to shifting the input vector r bits to the left. The algorithm chooses the checksum C so that T is divisible by a predefined polynomial P of degree r, called the generator polynomial.
The algorithm divides T by P, and sets the checksum equal to the binary vector corresponding to the remainder. That is, if T = Q×P + R, where R is a polynomial of degree less than r, the checksum is the binary vector corresponding to R. If necessary, the algorithm prepends zeros to the checksum so that it has length r.
The CRC generation feature, which implements the transmission phase of the CRC algorithm, does the following:
Left shifts the input data vector by r bits and divides the corresponding polynomial by P.
Sets the checksum equal to the binary vector of length r, corresponding to the remainder from step 1.
Appends the checksum to the input data vector. The result is the output vector.
The CRC detection feature computes the checksum for its entire input vector, as described above.
The CRC algorithm uses binary vectors to represent binary polynomials, in descending order of powers. For example, the vector [1 1 0 1] represents the polynomial x3 + x2 + 1.
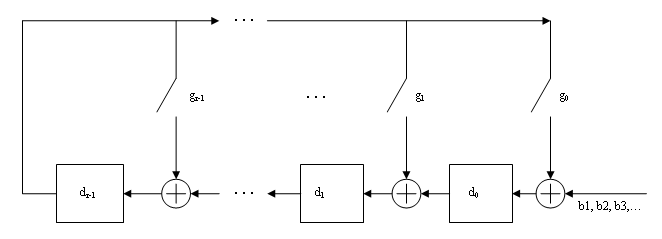
Bits enter the linear feedback shift register (LFSR) from the lowest index bit to the highest index bit. The sequence of input message bits represents the coefficients of a message polynomial in order of decreasing powers. The message vector is augmented with r zeros to flush out the LFSR, where r is the degree of the generator polynomial. If the output from the leftmost register stage d(1) is a 1, then the bits in the shift register are XORed with the coefficients of the generator polynomial. When the augmented message sequence is completely sent through the LFSR, the register contains the checksum [d(1) d(2) . . . d(r)]. This is an implementation of binary long division, in which the message sequence is the divisor (numerator) and the polynomial is the dividend (denominator). The CRC checksum is the remainder of the division operation.
Direct CRC Algorithm
This block diagram shows the direct CRC algorithm.
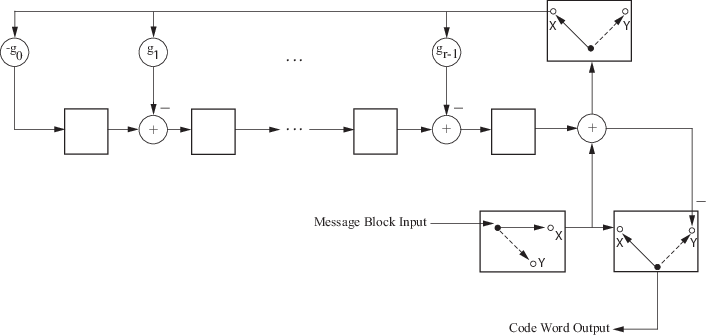
Where Message Block Input is and Code Word Output is
The initial step of the direct CRC encoding occurs with the three switches in position X. The algorithm feeds k message bits to the encoder. These bits are the first k bits of the code word output. Simultaneously, the algorithm sends k bits to the linear feedback shift register (LFSR). When the system completely feeds the kth message bit to the LFSR, the switches move to position Y. Here, the LFSR contains the mathematical remainder from the polynomial division. These bits are shifted out of the LFSR and they are the remaining bits (checksum) of the code word output.
The CRC syndrome detector outputs the received message frame and a checksum error vector according to the specified generator polynomial and number of checksums per frame.
The checksum bits are removed from each subframe so that the resulting output frame length is N – C×P, where N is the length of the received codeword column, C is the number of checksums per frame, and P is the degree of the generator polynomial. The input frame must be evenly divisible by C.
For a specific initial state of the internal shift register:
The received codeword is divided into C equal-sized subframes.
The CRC is removed from each of the C subframes and compared to the checksum calculated on the received codeword subframes.
The output frame is assembled by concatenating the subframe bits of the C subframes and then output as a column vector.
The checksum error is output as a binary column vector of length C. An element value of 0 indicates an error-free received subframe, and an element value of 1 indicates an error occurred in the received subframe.
For the scenario shown here, a 16-bit codeword is received with an error in the third bit, a z3 + z2 + 1 generator polynomial computes the CRC checksum, the initial state is 0, and the number of checksums per frame is 2.

Since the number of checksums per frame is 2 and the generator polynomial degree is 3, the
received codeword is split in half and two checksums of size 3 are computed, one for each
half of the received codeword. The initial states are not shown because an initial state of
[0] does not affect the output of the CRC algorithm. The output frame
contains the concatenation of the two halves of the received codeword as a single vector of
size 10. The checksum error signal output contains a 2-by-1 binary frame vector whose
entries should match the transmitted checksum. As shown in the figure, the first checksum
differs from the transmitted values and the second checksum matches the transmitted values.
This indicates an error occurred in reception of the first half of the codeword.
References
[1] Sklar, Bernard. Digital Communications: Fundamentals and Applications. Englewood Cliffs, N.J.: Prentice-Hall, 1988.
[2] Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Upper Saddle River, N.J.: Prentice Hall, 1995.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006a
See Also
Functions
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)