comm.IQImbalanceCompensator
Compensate for IQ imbalance
Description
The comm.IQImbalanceCompensator
System object™ compensates for the imbalance between the in-phase and quadrature (IQ)
components of a modulated signal. The adaptive algorithm inherent to the IQ imbalance
compensator is compatible with M-PSK, M-QAM, and OFDM
modulation schemes, where M>2. For more information, see Algorithms.
Note
The output of the compensator might be scaled and rotated, that is, multiplied by a complex number, relative to the reference constellation. In practice, this transformation is not an issue because, before demodulation, receivers correct for it by using channel estimation.
To compensate for IQ imbalance:
Create the
comm.IQImbalanceCompensatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
iqcomp = comm.IQImbalanceCompensator
iqcomp = comm.IQImbalanceCompensator(Name=Value)comm.IQImbalanceCompensator(CoefficientSource="Input port") specifies
that the compensator coefficients must be provided when you call the object. For this
configuration, all other properties are disabled.
Properties
Usage
Syntax
Description
y = iqcomp(x,c)c, instead of generating
them internally. This syntax applies when the CoefficientSource property
is set to Input port. When using this syntax, adaptive estimation of
the compensator coefficient is disabled.
y = iqcomp(x,s)s. This syntax applies when the StepSizeSource property is set
to Input port.
y = iqcomp(x,a)a, to enable or disable
coefficient updates. This syntax applies when the AdaptInputPort property is set
to true.
y = iqcomp(x,s,a)s, and the adaptation control signal,
a, to enable and disable coefficient updates. This syntax applies
when the StepSizeSource property is set
to Input port and the AdaptInputPort property is set
to true.
[
also returns estimated compensation coefficients with input arguments from any of the
previous syntaxes. This syntax applies when the y,coef] = iqcomp(x,___)CoefficientOutputPort
property is set to Input port.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
Imbalance between the in-phase and quadrature components of signal output from RF receivers can be cost-effectively compensated rather than improving the analog front-end RF hardware. Direct conversion receivers, in particular, introduce IQ imbalance. A circularity-based blind compensation algorithm is used as the basis for the IQ imbalance compensator.
A generalized IQ imbalance model is shown, where g is the amplitude imbalance and ϕ is the phase imbalance. For no impairment, g = 1 and ϕ = 0. In the figure, H(f) is the nominal frequency response of the branches due to, for example, low-pass filters. HI(f) and HQ(f) represent the portions of the in-phase and quadrature amplitude and phase responses that differ from the nominal response. With perfect matching, HI(f) = HQ(f) = 1.
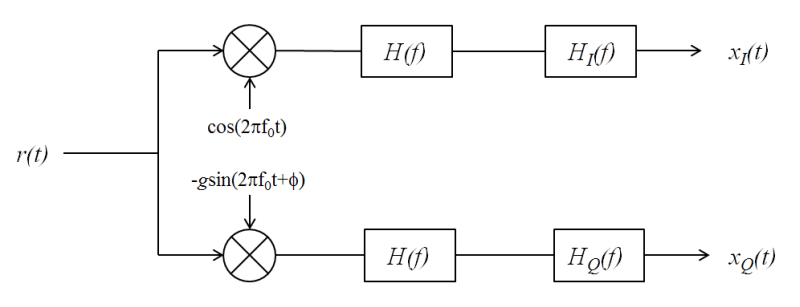
Let z(t) be the ideal baseband equivalent signal of the received signal, r(t), where its Fourier transform is denoted as Z(f). Given the generalized IQ imbalance model, the Fourier transform of the imbalanced signal, x(t) = xI(t) + xQ(t), is
where G1(f) and G2(f) are the direct and conjugate components of the IQ imbalance. These components are defined as
Applying the inverse Fourier transform to X(f), the signal model becomes x(t) = g1(t) × z(t) + g2(t) × z*(t).
This transformation suggests the compensator structure as shown in which discrete-time notation expresses the variables. The compensated signal is expressed as y(n) = x(n) + wx*(n).
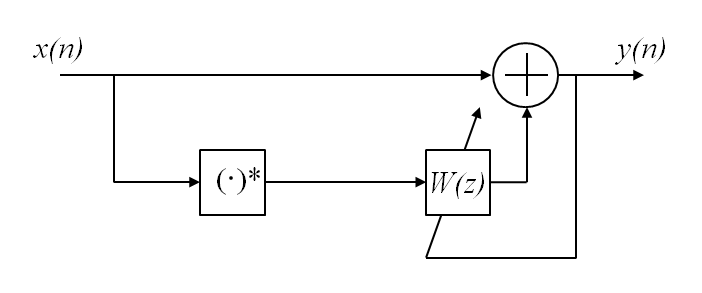
An algorithm of the form
is used to determine the weights because it ensures that the output is
proper, that is, the condition, E[y2(n)]
= 0 is satisfied. For further details, see [1]. The initial value
of w is determined by the initial compensator coefficient, which has a
default value of 0 + 0i. M is the adaptation step size
as described in StepSize.
References
[1] Anttila, L., M. Valkama, and M. Renfors. "Blind compensation of frequency-selective I/Q imbalances in quadrature radio receivers: Circularity-based approach.", Proc. IEEE® ICASSP (2007): III-245–48.
[2] Kiayani, A., L. Anttila, Y. Zou, and M. Valkama, "Advanced Receiver Design for Mitigating Multiple RF Impairments in OFDM Systems: Algorithms and RF Measurements." Journal of Electrical and Computer Engineering 2012.
Extended Capabilities
Version History
Introduced in R2014b




