Equalization, Convolution, and Cyclic Prefix Addition
This example introduces frequency domain equalization and shows how to convert circular convolution to linear convolution. When considering a linear channel model, the received signal is the convolution of the transmitted signal with the channel impulse response. In the frequency domain, the received signal is the linear convolution of the transmitted signal with the channel impulse response :
OFDM receivers use frequency domain equalization to recover the original transmitted signal, so that:
FFT processing yields the circular convolution of u with h. For the circular convolution of u and h to be equivalent to the linear convolution, u and h must be padded with zeros to a length of at least (length(u) + length(h) - 1) before you take the discrete Fourier transform (DFT). After you invert the product of the DFTs, retain only the first N + L - 1 elements. For an example that demonstrates this process, see the Linear and Circular Convolution topic.
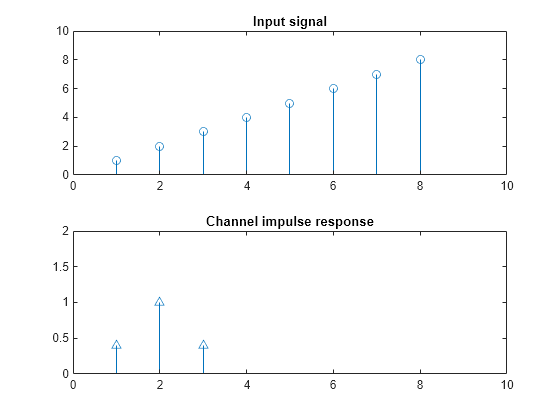
Define a short input signal, u1, and channel impulse response, h. The input signal must be longer than the channel impulse response. Display a stem plot of the signals.
u1 = 1:8; h = [0.4 1 0.4]; figure subplot(2,1,1) stem(u1); axis([0 10 0 10]) title("Input signal") subplot(2,1,2) stem(h,'^'); axis([0 10 0 2]) title("Channel impulse response")
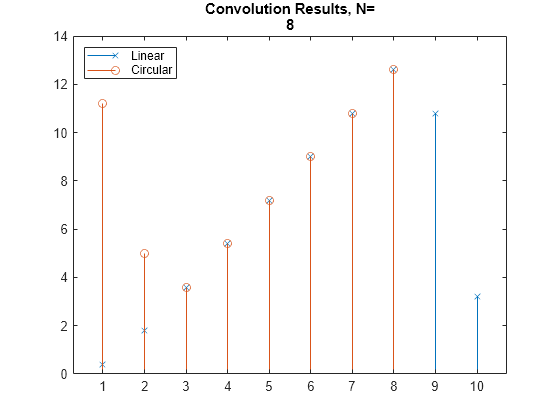
Compare the circular and linear convolution of u1 with h. Perform linear and circular convolution by using the conv and cconv functions, respectively. The smearing effects due to the nonideal channel cause the linear and circular convolution to yield different results at some points. A cyclic prefix (CP) enables effective use of OFDM in a nonideal channel with unknown propagation delay.
N = length(u1); yl1 = conv(u1,h); yc1 = cconv(u1,h,N); figure; stem(yl1,"x") hold on; stem(yc1,"o") title(["Convolution Results, N=",int2str(N)]) legend ("Linear","Circular","Location","northwest")
Add Cyclic Prefix (CP)
For OFDM processing, the necessary padding for the circular convolution is provided by adding a CP rather than zero-padding the signals. Adding a CP that repeats the end samples of the symbol enables:
Modeling of the linear convolution of a frequency-selective multipath channel as circular convolution
Use of an FFT to compute the convolution
Simple frequency domain processing for channel estimation, equalization, and synchronization
Repeated samples to be used in forward error correction schemes
L = length(h); % Length of channel N = length(u1); % Length of input signal ucp = u1(N-L+1:N); % Use last samples of input signal as the CP u2 = [ucp u1]; % Prepend the CP to the input signal yl2 = conv(u2,h); % Convolution of input+CP and channel yl2 = yl2(L+1:end); % Remove CP to compare signals figure; stem(yl2,"x") hold on; stem(yc1,"o") title("Convolution Results with Cyclic Prefix") legend ("Linear","Circular","Location","northwest")
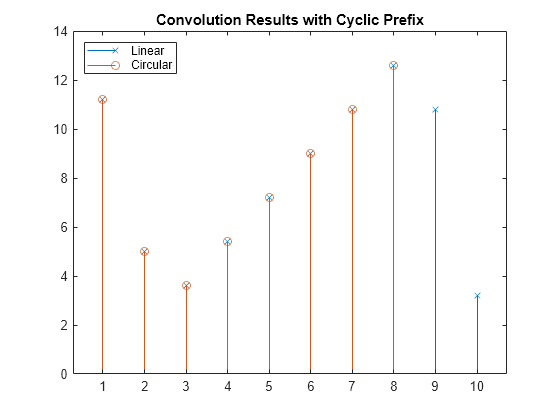
Compare the linear and circular convolution sequences.
if max(yc1 - yl2(1:N)) < 1e-8 disp("Linear and circular convolution sequences match.") else disp("Received symbols do not match transmitted symbols.") end
Linear and circular convolution sequences match.