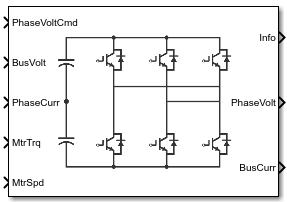
Three-Phase Voltage Source Inverter
Three-phase voltage source inverter
Libraries:
Powertrain Blockset /
Propulsion /
Electric Motors and Inverters
Description
The Three-Phase Voltage Source Inverter block implements a three-phase voltage source inverter that generates neutral voltage commands for a balanced three-phase load. Configure the voltage switching function for continuous vector modulation or inverter switch input signals. You can incorporate the block into a closed-loop model to simulate a power inverter. The block controls the ideal switch states.
To enable power loss calculations suitable for code generation targets that limit memory, select Enable memory optimized 2D LUT. Click Calibrate Maps to virtually calibrate an inverter power loss lookup table as a function of motor torque and motor speed.
If you select Input inverter temperature, click Calibrate Maps to virtually calibrate the power loss table as a function of motor torque, motor speed, and inverter temperature. You cannot enable memory optimization for the 3D power loss lookup table.
Use the Switching voltage function parameter to set the switching voltage function.
|
Setting |
Implementation |
Illustration |
|---|---|---|
|
Commanded phase voltage |
Phase a, b, c line-to-neutral voltage command input. Suitable for continuous sinusoidal or space vector modulation input signals. |
|
|
Switch inputs (default) |
Inverter switch input command. Suitable for hardware-in-the-loop (HIL) simulation. The inverter switches S1, S3, and S5 using complemented control for S2, S4, and S6. |
|
Virtual Calibration
If you have Model-Based Calibration Toolbox™, click Calibrate Maps to virtually calibrate the lookup tables using measured data. The dialog box steps through these tasks.
Task | Description | ||||||
|---|---|---|---|---|---|---|---|
Import Loss Data | Import this loss data from a file. For example, open
For more information, see Using Data (Model-Based Calibration Toolbox).
Collect inverter data at steady-state operating conditions. Data should cover the inverter speed, torque, and temperature operating range. To filter or edit the data, select Edit in Application. The Model-Based Calibration Toolbox Data Editor opens. | ||||||
Generate Response Models | Model-Based Calibration Toolbox uses test plans to fit data to Gaussian process models (GPMs). To assess or adjust the response model fit, select Edit in Application. The Model-Based Calibration Toolbox Model Browser opens. For more information, see Model Assessment (Model-Based Calibration Toolbox). | ||||||
Generate Calibration | Model-Based Calibration Toolbox calibrates the response models and generates calibrated tables. To assess or adjust the calibration, select Edit in Application. The Model-Based Calibration Toolbox CAGE Browser opens. For more information, see Calibration Lookup Tables (Model-Based Calibration Toolbox). | ||||||
Update block parameters | Update these parameters with the calibration.
|
Switching Function
For the switch voltage, the block implementation depends on the Switching voltage function setting.
| Setting | Calculation | Equations |
|---|---|---|
Commanded phase
voltage | Continuous line-to-neutral voltage commands set to phase a, b, c line-to-neutral voltage command input | |
Line-to-line voltage | ||
Switch inputs | Switching function | |
Line-to-center point voltage | ||
Line-to-neutral voltage | ||
Line-to-line voltage |
The equations use these variables.
SFa, SFb, SFc | Phase a, b, c line switching functions, respectively |
vbus | Power source bus voltage |
Vao, Vbo, Vco | Phase a, b, c line-to-center voltage, respectively |
Van, Vbn, Vcn | Phase a, b, c line-to-neutral voltage, respectively |
Vab, Vbc, Vca | Phase ab, bc, ca line-to-neutral voltage, respectively |
Va_cmd, Vb_cmd, Vc_cmd | Phase a, b, c line-to-neutral voltage commands, respectively |
Current and Power Loss
For the line-to-center, line-to-neutral, and line-to-line voltage, the block implements these equations.
| Calculation | Equations | |
|---|---|---|
| Motor and bus power | ||
Inverter power loss and bus current | ||
The equations use these variables.
| Pmtr | Power delivered to the motor |
Pbus | Power from input bus |
Ploss | Power loss |
ibus | Power source bus current |
ia, ib, ic | Phase a, b, c line current, respectively |
Van, Vbn, Vcn | Phase a, b, c line-to-neutral voltage, respectively |
vbus | Power source bus voltage |
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Variable | Equation | ||
|---|---|---|---|---|---|
|
|
| Power delivered to the motor | PTrnsfrdMtr | |
PwrBus | Power from input bus | PTrnsfrdBus | |||
|
| PwrLoss | Power loss Negative value indicates power loss | PNotTrnsfrd | ||
|
| Not used | ||||
Lookup Table Memory Optimization
The inverter power loss table parameter Corresponding power loss, ploss_table data is a function of motor torque and motor speed at different battery voltages. Positive current indicates battery discharge. Negative current indicates battery charge.
To enable power loss calculations suitable for code generation targets that limit memory, select Enable memory optimized 2D LUT. The block uses linear interpolation to optimize the inverter power loss lookup table values for code generation. This table summarizes the optimization implementation.
| Use Case | Implementation | |
|---|---|---|
Motor speed and torque input align with the lookup table breakpoint values. | Memory-optimized power loss is power loss lookup table value at intersection of motor speed and torque. | |
Motor speed and torque input do not align with the lookup table breakpoint values, but are within range. | Memory-optimized power loss is linear interpolation between corresponding motor speed and torque. | |
Motor speed and torque input do not align with the lookup table breakpoint values, and are out of range. | Cannot compute a memory-optimized power loss. Block uses extrapolated data. | |
The lookup tables optimized for code generation do not support extrapolation for data that is out of range. However, you can include pre-calculated extrapolation values in the power loss lookup table by selecting Specify Extrapolation.
The block uses the endpoint parameters to resize the table data.
| User Input | Extrapolation |
|---|---|
|
|
Ports
Input
Output
Parameters
References
[1] Lee, Byoung-Kuk and Mehrdad Ehsami. “A simplified functional simulation model for three-phase voltage-source inverter using switching function concept.” IEEE® Transactions on Industrial Electronics, Vol. 48, No. 2, pp. 309-321, April 2001.
[2] Ziogas, Phoivas D., Eduardo P. Wiechmann, and Victor R. Stefanovic. “A Computer-Aided Analysis and Design Approach for Static Voltage Source Inverters.” IEEE Transactions on Industrial Electronics Transactions on Industry Applications, Vol. IA-21, No. 5, September/October 1985.
Extended Capabilities
Version History
Introduced in R2019a