Time-Frequency Masking for Harmonic-Percussive Source Separation
Time-frequency masking is the process of applying weights to the bins of a time-frequency representation to enhance, diminish, or isolate portions of audio.
The goal of harmonic-percussive source separation (HPSS) is to decompose an audio signal into harmonic and percussive components. Applications of HPSS include audio remixing, improving the quality of chroma features, tempo estimation, and time-scale modification [1]. Another use of HPSS is as a parallel representation when creating a late fusion deep learning system. Many of the top performing systems of the Detection and Classification of Acoustic Scenes and Events (DCASE) 2017 and 2018 challenges used HPSS for this reason.
This example walks through the algorithm described in [1] to apply time-frequency masking to the task of harmonic-percussive source separation.
For an example of deriving time-frequency masks using deep learning, see Cocktail Party Source Separation Using Deep Learning Networks.
Create Harmonic-Percussive Mixture
Read in harmonic and percussive audio files. Both have a sample rate of 16 kHz.
[harmonicAudio,fs] = audioread("violin.wav"); percussiveAudio = audioread("drums.wav");
Listen to the harmonic signal and plot the spectrogram. Note that there is continuity along the horizontal (time) axis.
sound(harmonicAudio,fs) spectrogram(harmonicAudio,1024,512,1024,fs,"yaxis") title("Harmonic Audio")
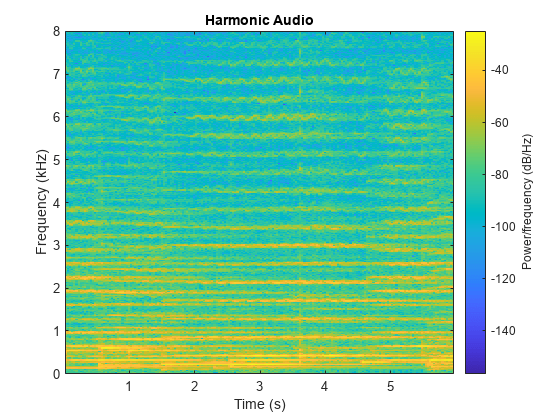
Listen to the percussive signal and plot the spectrogram. Note that there is continuity along the vertical (frequency) axis.
sound(percussiveAudio,fs) spectrogram(percussiveAudio,1024,512,1024,fs,"yaxis") title("Percussive Audio")
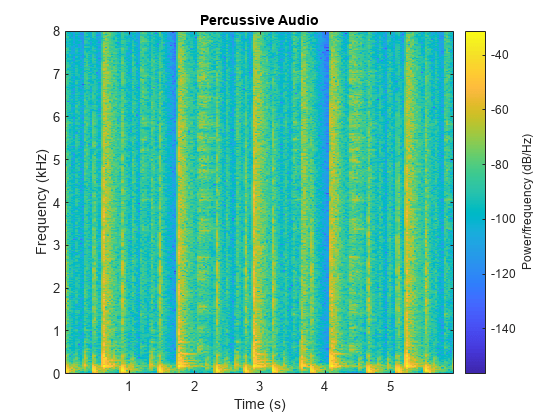
Mix the harmonic and percussive signals. Listen to the harmonic-percussive audio and plot the spectrogram.
mix = harmonicAudio + percussiveAudio; sound(mix,fs) spectrogram(mix,1024,512,1024,fs,"yaxis") title("Harmonic-Percussive Audio")

The HPSS proposed by [1] creates two enhanced spectrograms: a harmonic-enhanced spectrogram and a percussive-enhanced spectrogram. The harmonic-enhanced spectrogram is created by applying median filtering along the time axis. The percussive-enhanced spectrogram is created by applying median filtering along the frequency axis. The enhanced spectrograms are then compared to create harmonic and percussive time-frequency masks. In the simplest form, the masks are binary.
HPSS Using Binary Mask
Convert the mixed signal to a half-sided magnitude short-time Fourier transform (STFT).
win = sqrt(hann(1024,"periodic")); overlapLength = floor(numel(win)/2); fftLength = 2^nextpow2(numel(win) + 1); y = stft(mix,Window=win,OverlapLength=overlapLength,FFTLength=fftLength,FrequencyRange="onesided"); ymag = abs(y);
Apply median smoothing along the time axis to enhance the harmonic audio and diminish the percussive audio. Use a filter length of 200 ms, as suggested by [1]. Plot the power spectrum of the harmonic-enhanced audio.
timeFilterLength = 0.2; timeFilterLengthInSamples = timeFilterLength/((numel(win) - overlapLength)/fs); ymagharm = movmedian(ymag,timeFilterLengthInSamples,2); surf(log10(ymagharm.^2),EdgeColor="none") title("Harmonic Enhanced Audio") view([0,90]) axis tight
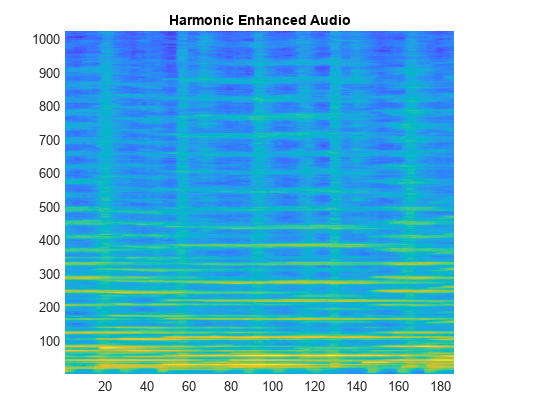
Apply median smoothing along the frequency axis to enhance the percussive audio and diminish the harmonic audio. Use a filter length of 500 Hz, as suggested by [1]. Plot the power spectrum of the percussive-enhanced audio.
frequencyFilterLength = 500; frequencyFilterLengthInSamples = frequencyFilterLength/(fs/fftLength); ymagperc = movmedian(ymag,frequencyFilterLengthInSamples,1); surf(log10(ymagperc.^2),EdgeColor="none") title("Percussive Enhanced Audio") view([0,90]) axis tight

To create a binary mask, first sum the percussive- and harmonic-enhanced spectrums to determine the total magnitude per bin.
totalMagnitudePerBin = ymagharm + ymagperc;
If the magnitude in a given harmonic-enhanced or percussive-enhanced bin accounts for more than half of the total magnitude of that bin, then assign that bin to the corresponding mask.
harmonicMask = ymagharm > (totalMagnitudePerBin*0.5); percussiveMask = ymagperc > (totalMagnitudePerBin*0.5);
Apply the harmonic and percussive masks and then return the masked audio to the time domain.
yharm = harmonicMask.*y; yperc = percussiveMask.*y;
Perform the inverse short-time Fourier transform to return the signals to the time domain.
h = istft(yharm,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided"); p = istft(yperc,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided");
Listen to the recovered harmonic audio and plot the spectrogram.
sound(h,fs) spectrogram(h,1024,512,1024,fs,"yaxis") title("Recovered Harmonic Audio")
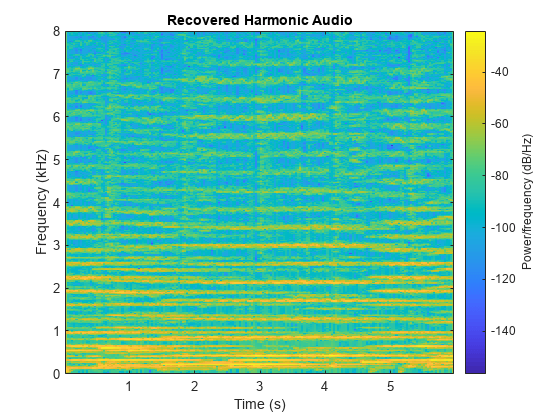
Listen to the recovered percussive audio and plot the spectrogram.
sound(p,fs) spectrogram(p,1024,512,1024,fs,"yaxis") title("Recovered Percussive Audio")
Plot the combination of the recovered harmonic and percussive spectrograms.
sound(h + p,fs) spectrogram(h + p,1024,512,1024,fs,"yaxis") title("Recovered Harmonic + Percussive Audio")
HPSS Using Binary Mask and Residual
As suggested in [1], decomposing a signal into harmonic and percussive sounds is often impossible. They propose adding a thresholding parameter: if the bin of the spectrogram is not clearly harmonic or percussive, categorize it as residual.
Perform the same steps described in HPSS Using Binary Mask to create harmonic-enhanced and percussive-enhanced spectrograms.
win = sqrt(hann(1024,"periodic")); overlapLength = floor(numel(win)/2); fftLength = 2^nextpow2(numel(win) + 1); y = stft(mix,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,FrequencyRange="onesided"); ymag = abs(y); timeFilterLength = 0.2; timeFilterLengthInSamples = timeFilterLength/((numel(win) - overlapLength)/fs); ymagharm = movmedian(ymag,timeFilterLengthInSamples,2); frequencyFilterLength = 500; frequencyFilterLengthInSamples = frequencyFilterLength/(fs/fftLength); ymagperc = movmedian(ymag,frequencyFilterLengthInSamples,1); totalMagnitudePerBin = ymagharm + ymagperc;
Using a threshold, create three binary masks: harmonic, percussive, and residual. Set the threshold to 0.65. This means that if the magnitude of a bin of the harmonic-enhanced spectrogram is 65% of the total magnitude for that bin, you assign that bin to the harmonic portion. If the magnitude of a bin of the percussive-enhanced spectrogram is 65% of the total magnitude for that bin, you assign that bin to the percussive portion. Otherwise, the bin is assigned to the residual portion. The optimal thresholding parameter depends on the harmonic-percussive mix and your application.
threshold =  0.65;
harmonicMask = ymagharm > (totalMagnitudePerBin*threshold);
percussiveMask = ymagperc > (totalMagnitudePerBin*threshold);
residualMask = ~(harmonicMask+percussiveMask);
0.65;
harmonicMask = ymagharm > (totalMagnitudePerBin*threshold);
percussiveMask = ymagperc > (totalMagnitudePerBin*threshold);
residualMask = ~(harmonicMask+percussiveMask);Perform the same steps described in HPSS Using Binary Mask to return the masked signals to the time domain.
yharm = harmonicMask.*y; yperc = percussiveMask.*y; yresi = residualMask.*y; h = istft(yharm,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided"); p = istft(yperc,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided"); r = istft(yresi,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided");
Listen to the recovered harmonic audio and plot the spectrogram.
sound(h,fs) spectrogram(h,1024,512,1024,fs,"yaxis") title("Recovered Harmonic Audio")
Listen to the recovered percussive audio and plot the spectrogram.
sound(p,fs) spectrogram(p,1024,512,1024,fs,"yaxis") title("Recovered Percussive Audio")

Listen to the recovered residual audio and plot the spectrogram.
sound(r,fs) spectrogram(r,1024,512,1024,fs,"yaxis") title("Recovered Residual Audio")
Listen to the combination of the harmonic, percussive, and residual signals and plot the spectrogram.
sound(h + p + r,fs) spectrogram(h + p + r,1024,512,1024,fs,"yaxis") title("Recovered Harmonic + Percussive + Residual Audio")

HPSS Using Soft Mask
For time-frequency masking, masks are generally either binary or soft. Soft masking separates the energy of the mixed bins into harmonic and percussive portions depending on the relative weights of their enhanced spectrograms.
Perform the same steps described in HPSS Using Binary Mask to create harmonic-enhanced and percussive-enhanced spectrograms.
win = sqrt(hann(1024,"periodic")); overlapLength = floor(numel(win)/2); fftLength = 2^nextpow2(numel(win) + 1); y = stft(mix,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,FrequencyRange="onesided"); ymag = abs(y); timeFilterLength = 0.2; timeFilterLengthInSamples = timeFilterLength/((numel(win)-overlapLength)/fs); ymagharm = movmedian(ymag,timeFilterLengthInSamples,2); frequencyFilterLength = 500; frequencyFilterLengthInSamples = frequencyFilterLength/(fs/fftLength); ymagperc = movmedian(ymag,frequencyFilterLengthInSamples,1); totalMagnitudePerBin = ymagharm + ymagperc;
Create soft masks that separate the bin energy to the harmonic and percussive portions relative to the weights of their enhanced spectrograms.
harmonicMask = ymagharm./totalMagnitudePerBin; percussiveMask = ymagperc./totalMagnitudePerBin;
Perform the same steps described in HPSS Using Binary Mask to return the masked signals to the time domain.
yharm = harmonicMask.*y; yperc = percussiveMask.*y; h = istft(yharm,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided"); p = istft(yperc,Window=win,OverlapLength=overlapLength, ... FFTLength=fftLength,ConjugateSymmetric=true,FrequencyRange="onesided");
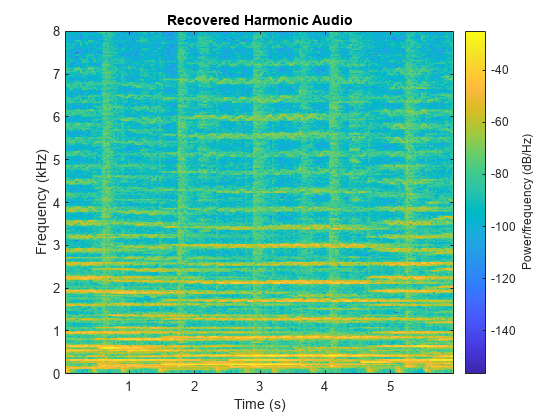
Listen to the recovered harmonic audio and plot the spectrogram.
sound(h,fs) spectrogram(h,1024,512,1024,fs,"yaxis") title("Recovered Harmonic Audio")
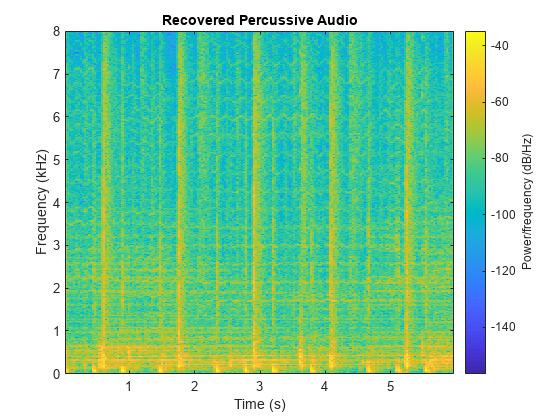
Listen to the recovered percussive audio and plot the spectrogram.
sound(p,fs) spectrogram(p,1024,512,1024,fs,"yaxis") title("Recovered Percussive Audio")
Example Function
The example function, HelperHPSS, provides the harmonic-percussive source separation capabilities described in this example. You can use it to quickly explore how parameters effect the algorithm performance.
help HelperHPSS [h,p] = HelperHPSS(x,fs) separates the input signal, x, into harmonic (h)
and percussive (p) portions. If x is input as a multichannel signal, it
is converted to mono before processing.
[h,p] = HelperHPSS(...,'TimeFilterLength',TIMEFILTERLENGTH) specifies the
median filter length along the time dimension of a spectrogram, in
seconds. If unspecified, TIMEFILTERLENGTH defaults to 0.2 seconds.
[h,p] = HelperHPSS(...,'FrequencyFilterLength',FREQUENCYFILTERLENGTH)
specifies the median filter length along the frequency dimension of a
spectrogram, in Hz. If unspecified, FREQUENCYFILTERLENGTH defaults to 500
Hz.
[h,p] = HelperHPSS(...,'MaskType',MASKTYPE) specifies the mask type as
'binary' or 'soft'. If unspecified, MASKTYPE defaults to 'binary'.
[h,p] = HelperHPSS(...,'Threshold',THRESHOLD) specifies the threshold of
the total energy for declaring an element as harmonic, percussive, or
residual. Specify THRESHOLD as a scalar in the range [0 1]. This
parameter is only valid if MaskType is set to 'binary'. If unspecified,
THRESHOLD defaults to 0.5.
[h,p] = HelperHPSS(...,'Window',WINDOW) specifies the analysis window
used in the STFT. If unspecified, WINDOW defaults to
sqrt(hann(1024,'periodic')).
[h,p] = HelperHPSS(...,'FFTLength',FFTLENGTH) specifies the number of
points in the DFT for each analysis window. If unspecified, FFTLENGTH
defaults to the number of elements in the WINDOW.
[h,p] = HelperHPSS(...,'OverlapLength',OVERLAPLENGTH) specifies the
overlap length of the analysis windows. If unspecified, OVERLAPLENGTH
defaults to 512.
[h,p,r] = HelperHPSS(...) returns the residual signal not classified as
harmonic or percussive.
Example:
% Load a sound file and listen to it.
[audio,fs] = audioread('Laughter-16-8-mono-4secs.wav');
sound(audio,fs)
% Call HelperHPSS to separate the audio into harmonic and percussive
% portions. Listen to the portions separately.
[h,p] = HelperHPSS(audio,fs);
sound(h,fs)
sound(p,fs)
HPSS Using Iterative Masking
[1] observed that a large frame size in the STFT calculation moves the energy towards the harmonic component, while a small frame size moves the energy towards the percussive component. [1] proposed using an iterative procedure to take advantage of this insight. In the iterative procedure:
Perform HPSS using a large frame size to isolate the harmonic component.
Sum the residual and percussive portions.
Perform HPSS using a small frame size to isolate the percussive component.
threshold1 =0.7; N1 =
4096; [h1,p1,r1] = HelperHPSS(mix,fs,Threshold=threshold1,Window=sqrt(hann(N1,"periodic")),OverlapLength=round(N1/2)); mix1 = p1 + r1; threshold2 =
0.6; N2 =
256; [h2,p2,r2] = HelperHPSS(mix1,fs,Threshold=threshold2,Window=sqrt(hann(N2,"periodic")),OverlapLength=round(N2/2)); h = h1; p = p2; r = h2 + r2;
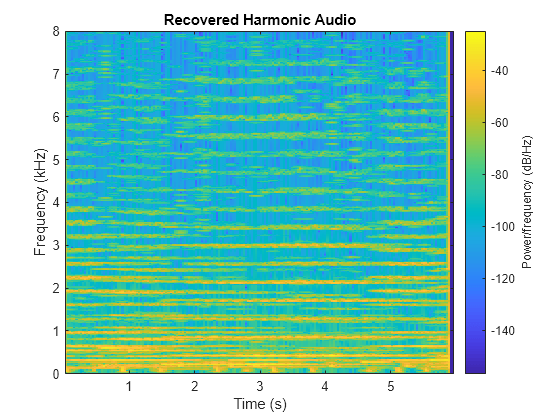
Listen to the recovered percussive audio and plot the spectrogram.
sound(h,fs) spectrogram(h,1024,512,1024,fs,"yaxis") title("Recovered Harmonic Audio")
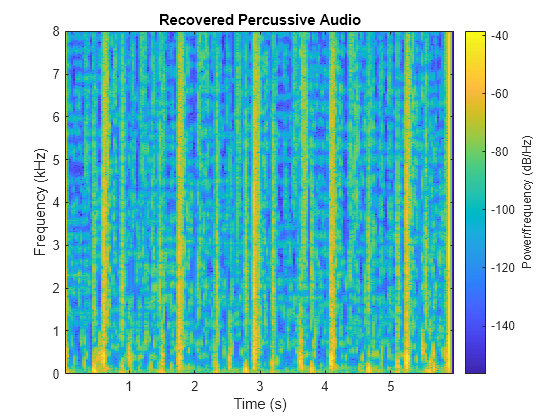
Listen to the recovered percussive audio and plot the spectrogram.
sound(p,fs) spectrogram(p,1024,512,1024,fs,"yaxis") title("Recovered Percussive Audio")
Listen to the recovered residual audio and plot the spectrogram.
sound(r,fs) spectrogram(r,1024,512,1024,fs,"yaxis") title("Recovered Residual Audio")

Listen to the combination of the harmonic, percussive, and residual signals and plot the spectrogram.
sound(h + p + r,fs) spectrogram(h+p+r,1024,512,1024,fs,"yaxis") title("Recovered Harmonic + Percussive + Residual Audio")

Enhanced Time Scale Modification Using HPSS
[2] proposes that time scale modification (TSM) can be improved by first separating a signal into harmonic and percussive portions and then applying a TSM algorithm optimal for the portion. After TSM, the signal is reconstituted by summing the stretched audio.
To listen to a stretched audio without HPSS, apply time-scale modification using the default stretchAudio function. By default, stretchAudio uses the phase vocoder algorithm.
alpha =  1.5;
mixStretched = stretchAudio(mix,alpha);
sound(mixStretched,fs)
1.5;
mixStretched = stretchAudio(mix,alpha);
sound(mixStretched,fs)Separate the harmonic-percussive mix into harmonic and percussive portions using HelperHPSS. As proposed in [2], use the default vocoder algorithm to stretch the harmonic portion and the WSOLA algorithm to stretch the percussive portion. Sum the stretched portions and listen to the results.
[h,p] = HelperHPSS(mix,fs);
hStretched = stretchAudio(h,alpha);
pStretched = stretchAudio(p,alpha,Method="wsola");
mixStretched = hStretched + pStretched;
sound(mixStretched,fs);References
[1] Driedger, J., M. Muller, and S. Disch. "Extending harmonic-percussive separation of audio signals." Proceedings of the International Society for Music Information Retrieval Conference. Vol. 15, 2014.
[2] Driedger, J., M. Muller, and S. Ewert. "Improving Time-Scale Modification of Music Signals Using Harmonic-Percussive Separation." IEEE Signal Processing Letters. Vol. 21. Issue 1. pp. 105-109, 2014.