Octave Filter Bank
Libraries:
Audio Toolbox /
Filters
Description
The Octave Filter Bank block decomposes a signal into octave or fractional-octave subbands. An octave-band is a frequency band where the highest frequency is twice the lowest frequency. Octave-band and fractional octave-band filters are commonly used to mimic how humans perceive loudness.
Examples
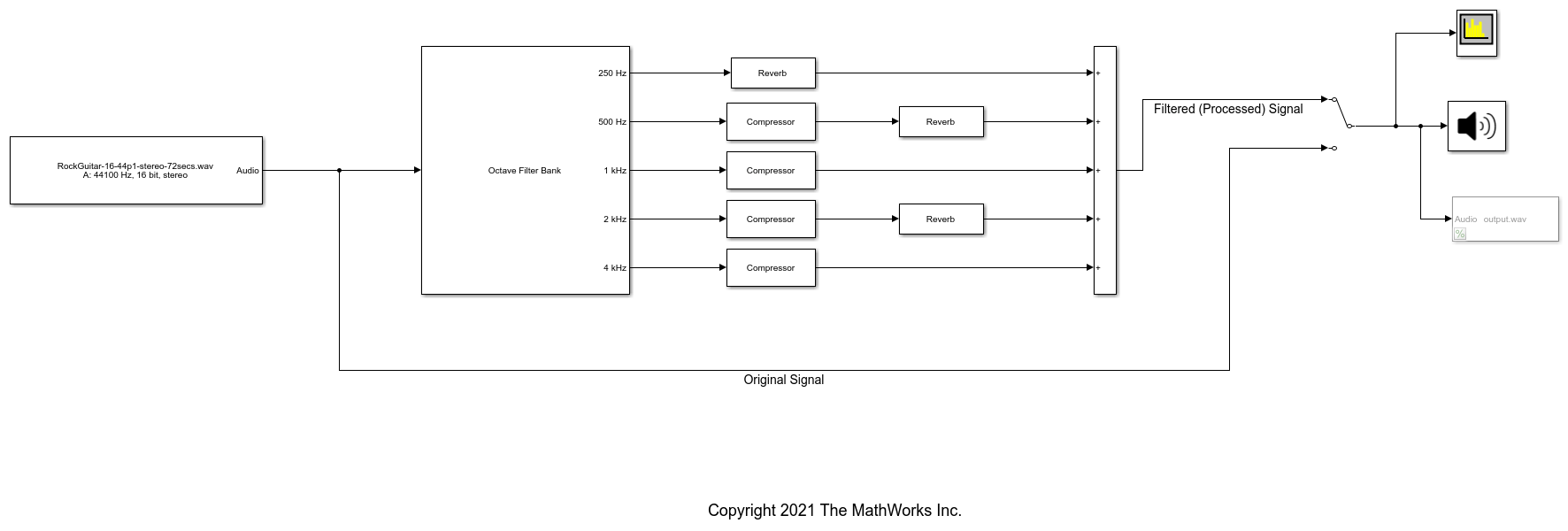
Use Octave Filter Bank to Create Flanging Chorus Effect for Guitar Layers (Overdubs)
Examine the Octave Filter Bank block in a Simulink® model. Apply octave band compression and reverb to create a flanging chorus effect on the guitar signal. Use the processed signal as an overdub layer to enhance your guitar recordings.
Ports
Input
Vector input –– The block treats the input as a single channel.
Matrix input –– The block treats each column of the input as an independent channel.
Data Types: single | double
Output
The Octave Filter Bank block outputs a signal with the same data type as the input signal. The shape of the output depends on the shape of the input, the number of filters in the bank, and whether or not you enable the Bands as separate output ports parameter.
If F is the number of filters in the bank, and the input signal is an L-by-C matrix, then the block returns an L-by-F-by-C array. If C is 1, then the block outputs a matrix.
Vector input –– When you provide a vector input, the block outputs an L-by-F matrix, where L is the number of elements in the vector and F is the number of filters in the bank.
Matrix input –– When you provide a matrix input, the block outputs a 3-D array with size L-by-F-by-C, where C is the number of channels in the matrix input.
Note
When you enable the Bands as separate output ports parameter, each output is the same size as the input.
Data Types: single | double
Parameters
Filter bandwidth in octaves, specified as 1 octave, 2/3
octave, 1/2 octave, 1/3 octave,
1/6 octave, 1/12 octave, 1/24
octave, 1/48 octave.
Frequency range of the filter bank in Hz, specified as a two-element row vector of positive monotonically increasing values. The block places filter bank center frequencies according to the Bandwidth (octaves), Reference frequency (Hz), and Octave ratio base parameters. Filters that have a center frequency outside of Frequency range (Hz) are ignored.
Reference frequency of the filter bank in Hz, specified as a positive integer scalar. The ANSI S1.11-2004 standard defines the center frequencies of the octave filters relative to the reference frequency. For more information, see Center Frequencies and Band Edges.
Order of the octave filters, specified as a positive even integer. The filter order applies to each individual filter in the bank.
Note
The default filter order for the octaveFilterBank object is 2.
Octave ratio base, specified as Base ten (ANSI S1.11
preferred) or Base two (musical scale). The
octave ratio base determines the distribution of the center frequencies of the octave
filters. The ANSI S1.11 standard recommends base 10. Base 2 is popular for music
applications. Base two (musical scale) defines an octave as a
factor of 2, and Base ten (ANSI S1.11 preferred) defines an octave
as a factor of 10 0.3.
When you select this parameter, the block inherits its sample rate from the input signal. When you clear this parameter, you specify the sample rate in the Input sample rate (Hz) parameter.
When you select this parameter, the block accepts the sample rate from the user.
Dependencies
To enable this parameter, clear the Inherit sample rate from input parameter.
When you select this parameter, the block provides an output port for each filter in the bank. Each output port is labeled with the center frequency of the filter and has a size identical to the input signal.
Code generation–– Simulate the model using generated C code. The first time you run a simulation, Simulink® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time.Interpreted execution–– Simulate the model using the MATLAB® interpreter. In this mode, you can debug the source code of the block.
Octave filters are best understood when viewed on a logarithmic scale, which models how the human ear weights the spectrum. The block uses a 2048-point FFT to calculate the magnitude response. The filter bank's response is displayed on a log-frequency scale with a legend to indicate the center frequency of each filter.
Name of the variable in the base workspace to contain the filter bank when it is exported. The name must be a valid MATLAB variable name.
When you select this parameter, exporting the filter bank overwrites the variable
specified by the Variable name parameter if it already exists in
the base workspace. If you do not select this parameter and the specified variable
already exists in the workspace, exporting the filter bank creates a new variable with
an underscore and a number appended to the variable name. For example, if the variable
name is var and it already exists, the exported variable will be
named var_1.
Export the filter bank to the base workspace in the variable specified by the Variable name parameter.
Tips
You cannot export the filter bank if you have enabled the Inherit sample rate from input parameter and the model is not running.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
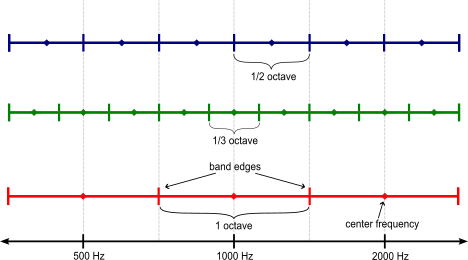
A band edge frequency refers to the lower or upper edge of the passband of a bandpass filter.
The center frequency of an octave filter is the geometric mean of the lower- and upper-band edge frequencies.
Algorithms
The Octave Filter Bank block is implemented as a parallel structure of
octave filters. Individual octave filters are designed as described by octaveFilter.
The ANSI S1.11-2004 standard [2] defines the center frequencies of the octave bands as
where:
fr is the reference frequency, which is specified by the Reference frequency (Hz) parameter.
G is the octave ratio, which is specified by the Octave ratio parameter.
b is the number of bands per octave, which is the inverse of the bandwidth of the filter in octaves. Specify the bandwidth with the Bandwidth (octaves) parameter.
k is any integer and represents the band number.
The center frequency definition differs depending on whether b is odd, such as for bandwidths of 1 octave or 1/3 octave, or even, such as for bandwidths of 1/2 octave or 1/6 octave. This ensures that the band edges of the whole octave band remain band edges for all of the fractional bands.
The upper and lower band edge frequencies are given by
The Octave Filter Bank block implements a higher-order digital bandpass filter design method as specified in [1].
In this design method, a desired digital bandpass filter maps to a Butterworth lowpass analog prototype, which is then mapped back to a digital bandpass filter:

The analog Butterworth filter is expressed as a cascade of second-order sections:
N is the filter order specified by the Filter order parameter.
The analog Butterworth filter is mapped to a digital filter using a bandpass version of the bilinear transformation:
where
This mapping results in the following substitution:
The analog prototype is evaluated:
Because s is second-order in z, the bandpass version of the bilinear transformation is fourth-order in z.
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 2010.
[2] Acoustical Society of America. American National Standard Specification for Octave-Band and Fractional-Octave-Band Analog and Digital Filters: ANSI S1.11-2004. Melville, NY: Acoustical Society of America, 2009.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2021a
See Also
octaveFilterBank | octaveFilter | weightingFilter | Weighting Filter | Octave Filter
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)