Antenna Near-Field Visualization
This example shows how to calculate and visualize the near-fields for antennas. Near fields can be plotted in Antenna Toolbox™ using the EHfields function. This function can also be used to calculate and plot the near-fields for antenna arrays. In the near field region, the electric and magnetic fields can exist independently of each other, and one type of field can dominate the other.
Create Dipole Antenna
Create a dipole antenna with default configuration.
ant = dipole; show(ant)

Define Points to Calculate Near-Field
The near fields are fields that are calculated in the close proximity of the antenna. This example plots the fields over a sphere of diameter 2 meters centered at the origin. The dipole length is also 2 meters and it is centered at the origin such that the sphere completely encloses the dipole. The sphere function generates 21-by-21 matrices for X, Y and Z. They are combined to generate 441 points as shown below.
[X, Y, Z] = sphere(20);
Points = [X(:), Y(:), Z(:)].';
plot3(Points(1,:), Points(2,:), Points(3,:), 'x');
Plot Near-Fields
The calculated near-fields at various points can be plotted by using the EHfields function as shown below. By default, both the electric and magnetic fields are plotted.
EHfields(ant, 70e6, Points);
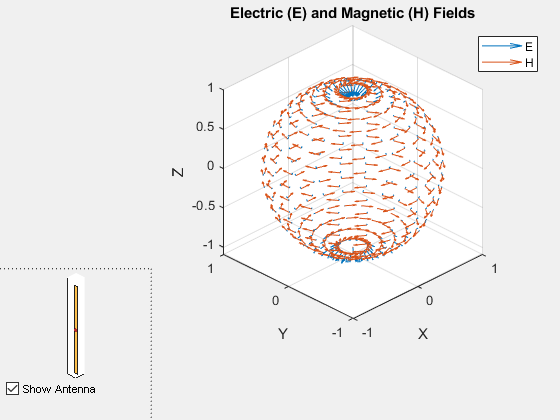
Individual E and H fields can be plotted by using the ViewField flag. The figure below shows the plot of magnetic field. As expected, the direction of the magnetic field follows the right hand rule due to the current along the length of the dipole.
EHfields(ant, 70e6, Points, ViewField="H");
Plot Electric Field
The below figure shows electric field distribution over the points in space. As expected, the electric field lines come out of the positive charge and go into the negative charge. The electric field forms loops along the length of the dipole. The ScaleFields flag is used to scale the size of the field vector. In this case, the electric field vector is multiplied by 2 to artificially increase the size of the vectors to make them clearly visible.
EHfields(ant, 70e6, Points, ViewField="E", ScaleFields=[2,0]);
Output Near-Fields to Workspace
By providing the output arguments, the electric and magnetic field values can be saved in the workspace to perform any other mathematical computations on them.
[E, H] = EHfields(ant, 70e6, Points);
The EHfields function, calculates the E-H fields at any point in space. It can be used to calculate the near or the far fields.
See Also
Modeling Resonant Coupled Wireless Power Transfer System | Wave Impedance