Space Rendezvous and Docking
This example shows the workflow required to plan maneuvers to enable a spacecraft in orbit to rendezvous and dock with another spacecraft. The rendezvous operation consists of a set of orbital maneuvers during which two spacecraft arrive at the same orbit and approach each other from close proximity. The target spacecraft is passive. The chaser spacecraft performs the maneuvers to rendezvous with the target. The docking maneuver consists of the chaser maneuvering further closer to the target and docking with it. In this example, the rendezvous maneuvers are planned using Optimization Toolbox™. The docking maneuver is performed by a closed loop controller that commands the force that needs to be provided by the translational reaction thrusters along each body axis of the chaser. The mission is simulated in Simulink® software and visualized in a satellite scenario. This example uses:
Aerospace Blockset™ Spacecraft Dynamics block
Aerospace Blockset Attitude Profile block
Aerospace Toolbox
satelliteScenarioobjectOptimization Toolbox™
fsolvefunctionOptimization Toolbox
fminconfunctionStateflow® Chart block
Mission Overview
The mission consists of two phases, rendezvous and docking.
Rendezvous Phase
The rendezvous phase consists of a series of maneuvers that enables the chaser to approach the target to a very close distance. Before rendezvous can commence, the initial orbit of the chaser and target must be on the same plane. This alignment is typically accomplished by timing the launch of the chaser so that the chaser is inserted into the correct orbital plane. Otherwise, plane change maneuvers must be performed at the intersection of the chaser and target orbital planes, which typically incurs a substantial delta-v cost. Assuming the orbital planes are aligned, rendezvous can be performed by placing the chaser on a phasing orbit. The phasing orbit approaches close to the target orbit (in the order of a few kilometers) and has a slightly different orbital period. Because of the difference in the orbital periods, the chaser and the target approach closer to one another after each orbit. If the insertion into the phasing orbit is timed correctly, after several orbits, both chaser and target will arrive at the closest point in their respective orbits at the same time. Upon arrival at this point, rendezvous has been accomplished.
This animation shows the rendezvous sequence.

The chaser is initially on a lower orbit compared to the target.
The first maneuver places the chaser on the phasing orbit. After several orbits, the chaser and the target approach close to one another.
When the chaser and the target are at their closest, the chaser performs a second maneuver to cancel out the relative velocity.
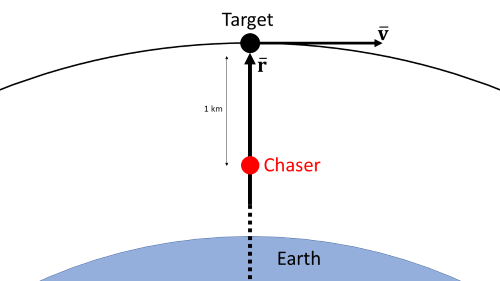
The rendezvous conditions require the chaser to be placed 1 km below the target along the radial position vector, , of the target. In addition, the relative velocity between the two spacecraft must be 0 m/s. From this point, the docking operations commence. In the diagram, is the ICRF velocity of the target. At the instant rendezvous is accomplished, the velocity of the chaser must also equal .
Docking Phase
After rendezvous is accomplished, docking operations are commenced in three phases:
Initial approach: The initial approach or R-bar approach, requires the chaser to move toward the target along the radial position vector, or , of the target using translational thrusters at about 0.3 m/s. During this phase, the relative distance is brought down to 100 m. The R-bar approach requires the relative velocity component of the chaser with respect to the target that is perpendicular to to be maintained at 0. As the chaser approaches the target from below, its orbital angular velocity drops. The chaser compensates by firing the translational thrusters perpendicular to . If the thrusters fail, the chaser starts lagging behind the target. This lag is an inherent safety feature of the R-bar approach because it eliminates the possibility of a collision with the target if the chaser thrusters fail.

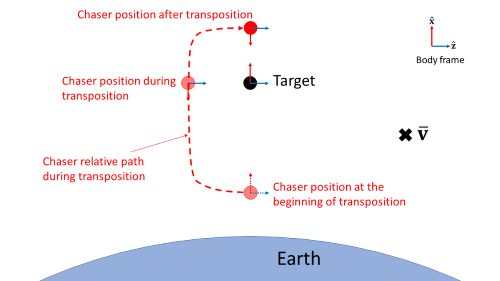
Transposition: The chaser reorients to docking attitude and maneuvers around the target to position itself about 20 m in front of the docking port of the target. If the attitude of the target is such that a direct path between the initial and final position during the transposition phase causes a collision, the chaser maneuvers around the target. The maneuver is done such that the target is offset by 20 m along the body z axis of the chaser. The offset about the body y axis of the chaser is always commanded to be 0 m. As a result, the transposition maneuver happens on the x-z plane of the body frame of the chaser while it is in its docking attitude.
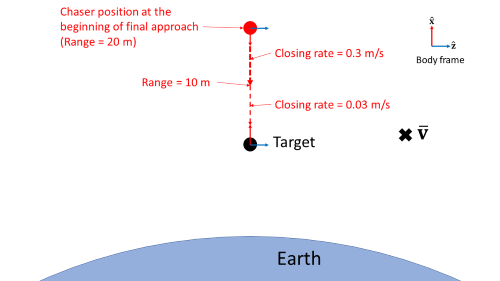
Final approach: The chaser closes in on the target at 0.3 m/s. When the range to the target reaches 10 m, the chaser reduces its closing rate to 0.03 m/s until their respective docking ports meet each other.
Mission Setup
The mission begins on August 8, 2022, 12:00 AM UTC.
epochYear = 2022;
epochMonth = 8;
epochDay = 6;
epochHour = 0;
epochMinute = 0;
epochSecond = 0;
epoch = datetime(epochYear,epochMonth,epochDay, ...
epochHour,epochMinute,epochSecond);The initial orbital elements of the chaser are:
Semimajor axis () = 7,500 km
Eccentricity = 0.001
Inclination = 30.1 degrees
Right ascension of ascending node = 60.1 degrees
Argument of periapsis = 120 degrees
True anomaly = 30 degrees
initialChaserSemimajorAxis = 7500000; % m initialChaserEccentricity = 0.001; initialChaserInclination = 30.1; % deg initialChaserRightAscensionofAscendingNode = 60.1; % deg initialChaserArgumentOfPeriapsis = 120; % deg initialChaserTrueAnomaly = 30; % deg initialChaserOscullatingElements = [initialChaserSemimajorAxis, ... initialChaserEccentricity, ... initialChaserInclination, ... initialChaserRightAscensionofAscendingNode, ... initialChaserArgumentOfPeriapsis, ... initialChaserTrueAnomaly];
The initial orbital elements of the target are:
Semimajor axis () = 8,000 km
Eccentricity = 0.0005
Inclination = 30 degrees
Right ascension of ascending node = 60 degrees
Argument of periapsis = 120 degrees
True anomaly = 310 degrees
initialTargetSemimajorAxis = 8000000; % m initialTargetEccentricity = 0.0005; initialTargetInclination = 30; % deg initialTargetRightAscensionofAscendingNode = 60; % deg initialTargetArgumentOfPeriapsis = 120; % deg initialTargetTrueAnomaly = 310; % deg initialTargetOscullatingElements = [initialTargetSemimajorAxis, ... initialTargetEccentricity, ... initialTargetInclination, ... initialTargetRightAscensionofAscendingNode, ... initialTargetArgumentOfPeriapsis, ... initialTargetTrueAnomaly];
Both spacecraft control their attitude by aligning their x-axes towards the commanded direction, which is the primary constraint vector. Therefore, the x-axis of each spacecraft constitutes the primary alignment vector.
primaryAlignmentVector = [1;0;0];
The spacecraft also attempt to minimize the alignment of their z axes towards a secondary direction, which is the secondary constraint vector. Therefore, the z axis of each spacecraft constitutes the secondary alignment vector.
secondaryAlignmentVector = [0;0;1];
Throughout the mission, the target spacecraft body axis remains aligned with the International Celestial Reference Frame (ICRF). Therefore, the primary and secondary constraint vectors for the target spacecraft are the ICRF x- and z- axes respectively.
primaryConstraintVectorTarget = [1;0;0]; secondaryConstraintVectorTarget= [0;0;1];
Accordingly, calculate the scalar-first quaternion of the target spacecraft using the SpaceRendezvousAndDockingExampleCalculateAttitude helper function.
targetAttitude = SpaceRendezvousAndDockingExampleCalculateAttitude( ... primaryAlignmentVector, ... primaryConstraintVectorTarget, ... secondaryAlignmentVector, ... secondaryConstraintVectorTarget);
The primary and secondary constraint vectors for the chaser are dependent on the mission phase.

The rendezvous condition requires the chaser to position itself 1 km below the target spacecraft along the target's radial position vector. The relative velocity between the two must be 0.
finalRelativeRadialDiscance = -1000; % m finalRelativeVelocityICRF = [0;0;0]; % m/s
The chaser must achieve rendezvous conditions using two maneuvers. Between the two maneuvers, the chaser is in coast phase. After the second maneuver is complete, the rendezvous conditions must be satisfied. During the coast phase, the periapsis of the chaser must not dip below 6578.137 km, which translates to an altitude of roughly 200 km.
minimumChaserPeriapsisBetweenBurns = 6578137; % mThe maneuvers must meet these conditions:
• For each maneuver, the delta-v components must not exceed 300 m/s.
• The first maneuver must be performed no earlier than 200 s after mission start time to allow for the chaser attitude to stabilize for the first maneuver.
• The first maneuver must be performed no later than one day after the mission start time.
• The second maneuver must be performed no later than one day after the first maneuver.
lowerBoundForFirstBurnTime = 200; % s lowerBoundForDeltaV = [-300;-300;-300]; % m/s lowerBoundForSecondBurnTimeAfterFirstBurn = 0; % s upperBoundForFirstBurnTime = 24*3600; % s upperBoundForDeltaV = [300;300;300]; % m/s upperBoundForSecondBurnTimeAfterFirstBurn = 24*3600; % s
After the rendezvous conditions are satisfied, the chaser enters docking phase. During the initial approach, the closing rate is 0.3 m/s.
initialApproachClosingRate = 0.3; % m/sDuring transposition, if the direct path between initial and final position of chaser poses a risk of collision, the chaser maneuvers around the target so that the target is offset by 20 m along the body z-axis of the chaser. After transposition, the chaser must be positioned 20 m in front of the target.
collisionAvoidanceZOffset = 20; % m transpositionFinalPosition = [20;0;0]; % m
During final approach, the closing rate is 0.3 m/s when the range to target is greater than 10 m, and 0.03 m/s otherwise.
finalApproachClosingRate1 = 0.3; % m/s finalApproachClosingRate2 = 0.03; % m/s
Optimization of Maneuvers
You can calculate the maneuvers required to facilitate rendezvous are calculated using Optimization Toolbox. The rendezvous maneuvers involve firing the main propulsion system and are approximated as impulsive maneuvers. You can formulate the rendezvous problem as a nonlinear constrained optimization problem. The goal of the problem is to minimize the delta-v magnitude caused by the impulsive maneuvers while satisfying the constraints defined by:
Rendezvous conditions specified by relative position and velocity between the chaser and the target
Periapsis constraint on the chaser between the maneuvers
Lower and upper bounds on delta-v components and times when the maneuvers are performed
The design variables of the optimization problem are the maneuver parameters consisting of:
First burn time
Delta-v for first burn along ICRF x-axis
Delta-v for first burn along ICRF y-axis
Delta-v for first burn along ICRF z-axis
Second burn time counted from the first burn time
Delta-v for second burn along ICRF x-axis
Delta-v for second burn along ICRF y-axis
Delta-v for second burn along ICRF z-axis
To aid in solution convergence, the position, velocity, and time are scaled to ensure that their magnitudes are roughly of the same order.
scaleTime = 50000; % s scalePos = 6378137; % m scaleVel = 8000; % m/s
Define the scaled lower and upper bounds on the maneuver parameters.
maneuverParameterLowerBound = ... [lowerBoundForFirstBurnTime/scaleTime; ... lowerBoundForDeltaV/scaleVel; ... lowerBoundForSecondBurnTimeAfterFirstBurn/scaleTime; ... lowerBoundForDeltaV/scaleVel]; maneuverParameterUpperBound = ... [upperBoundForFirstBurnTime/scaleTime; ... upperBoundForDeltaV/scaleVel; ... upperBoundForSecondBurnTimeAfterFirstBurn/scaleTime; ... upperBoundForDeltaV/scaleVel];
The sum of norm-squared of each delta-v constitutes the objective function and is defined in the file SpaceRendezvousAndDockingExampleObjectiveFcn.m. The nonlinear equality constraints defined by the rendezvous conditions and the nonlinear inequality constraint defined by the periapsis of the chaser between the rendezvous maneuvers are defined in the file SpaceRendezvousAndDockingExampleConstraintFcn.m.
This example performs the optimization using the fmincon function, which requires linear equality and inequality constraints to be defined. Because the defined optimization problem defined above does not contain such linear constraints, assign empty values to these.
linearInequalityConstraintA = []; linearInequalityConstraintb = []; linearEqualityConstraintA = []; linearEqualityConstraintb = [];
You must supply fmincon with a guess for the optimal maneuver parameters. If this initial guess is arbitrary, fmincon may not converge to a solution. To mitigate this outcome, generate the initial guess using the fsolve function, in which no optimization is performed and the inequality constraints and bounds on the maneuver parameters are ignored. You can reformulate the optimization problem to just satisfy the equality constraints in the file SpaceRendezvousAndDockingExampleConstraintFcn.m. This reduces the optimization problem to a root solving problem. Note that fsolve also requires an initial guess. However, because the root solving problem has no inequality constraints or bounds on the maneuver parameters, you can solve it using fsolve with relative ease, even with an arbitrary initial guess. The solution of the root solving problem is usually a good initial guess for the original optimization problem because it already obeys the orbital mechanics and satisfies the equality constraints.
Define the arbitrary initial guess for fsolve.
firstBurnTime = 200; % s firstDeltaV = [100;100;100]; % m/s secondBurnTimeAfterFirstBurn = 80000; % s secondDeltaV = [100;100;100]; % m/s initialGuess = [firstBurnTime/scaleTime; ... firstDeltaV/scaleVel; ... secondBurnTimeAfterFirstBurn/scaleTime; ... secondDeltaV/scaleVel];
Define fsolve configuration using optimoptions.
options = optimoptions( ... 'fsolve', ... MaxFunctionEvaluations = 1000000, ... MaxIterations = 10000, ... Algorithm = 'levenberg-marquardt', ... FunctionTolerance = 1e-6, ... StepTolerance = 1e-10);
Calculate the maneuver parameters using fsolve. The root solving problem often has multiple solutions. The actual solution that fsolve converges to depends on the initial guess.
needToReturnInequalityConstraint = false; maneuver = fsolve( ... @SpaceRendezvousAndDockingExampleConstraintFcn, ... initialGuess, ... options, ... epoch, ... initialChaserOscullatingElements, ... initialTargetOscullatingElements, ... finalRelativeRadialDiscance, ... finalRelativeVelocityICRF, ... minimumChaserPeriapsisBetweenBurns, ... needToReturnInequalityConstraint, ... scalePos, ... scaleVel, ... scaleTime);
Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
The initial guess for fmincon is the solution of fsolve.
initialGuess = maneuver;
Define fmincon configuration parameters using optmimoptions.
options = optimoptions( ... 'fmincon', ... Algorithm = 'sqp',... MaxFunctionEvaluations = 1000000, ... MaxIterations = 10000, ... StepTolerance = eps, ... OptimalityTolerance = 1e-2);
Calculate the optimal maneuver parameters using fmincon. The optimization problem contains multiple local minima. fmincon converges to one of these minima depending on the initial guess provided by fsolve, which in turn depends on the arbitrary initial guess provided to fsolve.
needToReturnInequalityConstraint = true; optimizedManeuver = fmincon( ... @SpaceRendezvousAndDockingExampleObjectiveFcn, ... initialGuess, ... linearInequalityConstraintA, ... linearInequalityConstraintb, ... linearEqualityConstraintA, ... linearEqualityConstraintb, ... maneuverParameterLowerBound, ... maneuverParameterUpperBound, ... @SpaceRendezvousAndDockingExampleConstraintFcn, ... options, ... epoch, ... initialChaserOscullatingElements, ... initialTargetOscullatingElements, ... finalRelativeRadialDiscance, ... finalRelativeVelocityICRF, ... minimumChaserPeriapsisBetweenBurns, ... needToReturnInequalityConstraint, ... scalePos, ... scaleVel, ... scaleTime);
Rendezvous Maneuver Parameter Extraction
Extract the rendezvous maneuver parameters to calculate the burn direction and duration for each maneuver.
Extract the maneuver times for each rendezvous maneuver. These times constitute the respective burn start time for each maneuver.
burnTime1 = optimizedManeuver(1)*scaleTime; burnTime2 = (optimizedManeuver(1) + optimizedManeuver(5))*scaleTime;
Extract the delta-v vectors for each maneuver.
deltaV1Vector = optimizedManeuver(2:4)*scaleVel; deltaV2Vector = optimizedManeuver(6:8)*scaleVel;
Calculate the delta-v magnitudes for each maneuver.
deltaV1 = norm(deltaV1Vector); deltaV2 = norm(deltaV2Vector);
Calculate the burn directions in ICRF for each rendezvous maneuver. These directions are simply the unit vector along each delta-v vector.
burnDirection1 = deltaV1Vector/norm(deltaV1Vector); burnDirection2 = deltaV2Vector/norm(deltaV2Vector);
The rendezvous maneuvers calculated by fmincon assume impulsive maneuvers, in which the delta-v is achieved instantaneously. To approximate an impulsive maneuver in Simulink model, assume a large propellant mass flow rate for the main propulsion system.
mDot = 7500; % kg/sDefine the initial chaser mass and specific impulse of the main propulsion system. The values are required to calculate the burn durations for each rendezvous maneuver.
m0 = 1000; % kg Isp = 400; % s
Calculate the main propulsion system exhaust velocity, which will be used to calculate chaser mass after each rendezvous maneuver burn.
ve = 9.81*Isp; % m/sCalculate the chaser mass after the first maneuver burn.
m1 = m0/exp(deltaV1/ve);
Calculate the chaser mass after the second maneuver burn.
m2 = m1/exp(deltaV2/ve);
Using the change in mass after each burn and the mass flow rate, calculate the burn duration for each maneuver.
burnDuration1 = (m0-m1)/mDot; burnDuration2 = (m1-m2)/mDot;
Mission Simulation
Open the simulation model.
model = 'SpaceRendezvousAndDockingExample.slx';
open_system(model);The top-level model consists of the Target spacecraft, Chaser spacecraft, and Simulation termination criterion subsystem. The Chaser spacecraft and Target spacecraft subsystems implement spacecraft dynamics and their respective guidance and control systems. The Simulation termination criterion subsystem ends the simulation when the distance between the chaser and the target is 1 m.

Both Chaser spacecraft and Target spacecraft subsystems consist of a Guidance and control subsystem and a Spacecraft subsystem. The Guidance and control subsystem of the chaser provides:
• Burn commands for the main propulsion system during the rendezvous phase
• Body force commands that the reaction control thrusters provide during the rendezvous phase
• Body moment commands that the reaction control thrusters provide to orient the chaser

The Guidance and control subsystem of the target only provides body moment commands to the Spacecraft subsystem, as illustrated below. This is because the target does not perform any maneuvers and only maintains a constant attitude with respect to ICRF.
The Spacecraft subsystems of the chaser and the target implement the spacecraft dynamics using the Spacecraft Dynamics block, which accepts the body moment inputs. The Spacecraft subsystem of the chaser also accepts body force, mass flow rate, and exhaust velocity inputs, as the image shows.

The mass flow rate and exhaust velocity inputs represent the main propulsion system, in which the mass changes when burning the engine. The body force and moment inputs represent the net thrust and moment that the reaction control thrusters must produce. The software ignores the mass change resulting from firing the thrusters.
The Guidance and control subsystems of the chaser and the target implement the guidance and control logic. Because the target does not perform any maneuvers and maintains a constant attitude with respect to ICRF, its Guidance and control subsystem only implements the rotational guidance and control systems. The Guidance and control subsystem of the chaser implements both translational and rotational guidance and control logics and issues the burn commands for the main propulsion system, as the image shows.

The Guidance subsystem issues burn commands during the rendezvous phase and translational guidance commands during the docking phase. The subsystem also provides rotational guidance throughout the mission. The translational guidance consists of the commanded relative velocity of the target with respect to the chaser in the body frame of the chaser. The rotational guidance consists of the commanded primary and secondary constraint vectors. The Guidance subsystem uses a Stateflow chart called Maneuver selector to implement the logic to determine which rendezvous maneuver must be executed and when to activate the docking phase, as the image shows.


The Maneuver subsystem implements the guidance logic during the rendezvous and docking phases using the Rendezvous subsystem and the Docking subsystem, respectively. The Docking subsystem consists of the Docking phase selector and Docking phase guidance subsystems, as the image shows.

The Docking phase guidance subsystem implements the guidance logic for the different docking phases. The Docking phase selector subsystem uses a Stateflow chart called Docking phase selector to implement the logic to select the appropriate docking phase, as the image shows.


The guidance commands are fed into the control system. The target spacecraft contains a rotational controller that is implemented by the Rotational controller subsystem. The chaser spacecraft consists of a translational and a rotational controller, which are implemented by the Control subsystem, as the image shows.

The Translational controller subsystem is only active during the docking phase. It accepts the translational guidance commands and calculates the body force that the reaction control system must produce using a proportional controller. The Rotational controller subsystem accepts the rotational guidance commands and calculates the body moments that the reaction control system must provide. The Rotational controller architecture of the chaser and the target is the same and represents a PD controller, as the image shows.
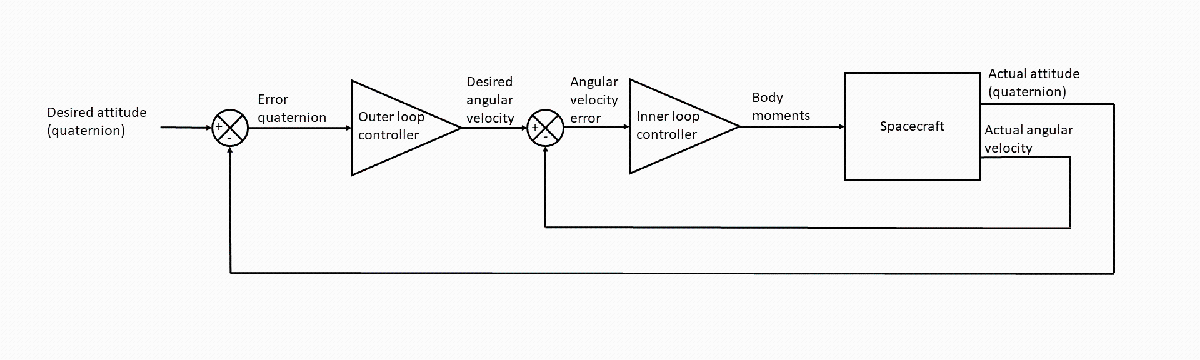
The Rotational controller subsystem of the chaser implements this architecture.

The Attitude Profile block calculates the error quaternion based on the current attitude of the spacecraft and the desired attitude deduced from the rotational guidance commands, which in turn consist of the primary and secondary constraint vectors.
Specify a default end time for the simulation. Because the stop time is unknown ahead of the simulation, it is arbitrarily set to 100,000 s after the second burn time. The assumption is that 100,000 s provides sufficient time to complete the docking phase. The actual simulation end time will be lower than this value if the stopping criterion is met sooner.
endTime = burnTime2 + 100000;
Simulate the model. The model is configured to run in rapid accelerator mode for performance.
simOut = sim('SpaceRendezvousAndDockingExample.slx');Visualize Mission in Satellite Scenario Viewer
The top-level Simulink model sends the ICRF position and attitude of the chaser and the target to the workspace in timeseries format. Use this data to set up a satellite scenario and visualize the mission. Create a satellite scenario object. Set the start and stop times to those of the mission. Set the sample time such that there are 35,311 time samples in the scenario, which roughly translates to a scenario sample time of 2.5 s.
startTime = epoch; stopTime = startTime + seconds(simOut.tout(end)); sampleTime = seconds(stopTime - startTime)/35311; sc = satelliteScenario(startTime,stopTime,sampleTime)
sc =
satelliteScenario with properties:
StartTime: 06-Aug-2022
StopTime: 07-Aug-2022 00:31:18
SampleTime: 2.5000
AutoSimulate: 1
Satellites: [1×0 matlabshared.satellitescenario.Satellite]
GroundStations: [1×0 matlabshared.satellitescenario.GroundStation]
Platforms: [1×0 matlabshared.satellitescenario.Platform]
Viewers: [0×0 matlabshared.satellitescenario.Viewer]
AutoShow: 1
Extract the ICRF position and attitude history of the chaser and target.
chaserPos = simOut.yout{1}.Values;
chaserAtt = simOut.yout{2}.Values;
targetPos = simOut.yout{3}.Values;
targetAtt = simOut.yout{4}.Values;Add the chaser spacecraft and define its attitude profile. Add a conical sensor 0.5 m in front of the chaser to mimic the docking port of the chaser.
chaser = satellite(sc,chaserPos,Name='Chaser');
pointAt(chaser,chaserAtt);
chaserDockingPort = conicalSensor(chaser,MountingLocation=[0.5;0;0]);Add the target spacecraft and define its attitude profile. Add a conical sensor 0.5 m in front of the target to mimic the docking port of the target.
target = satellite(sc,targetPos,Name='Target');
pointAt(target,targetAtt);
targetDockingPort = conicalSensor(target,MountingLocation=[0.5;0;0]);Launch a satellite scenario viewer and set the camera reference frame to 'Inertial'. Assign 3-D models to the chaser and target, visualize their coordinate axes and hide their orbits.
v = satelliteScenarioViewer(sc,CameraReferenceFrame='Inertial'); chaser.Visual3DModel = "SmallSat.glb"; chaser.Visual3DModelScale = 0.8; target.Visual3DModel = "SmallSat.glb"; target.Visual3DModelScale = 0.8; coordinateAxes([chaser target],Scale=2); hide(chaser.Orbit); hide(target.Orbit);
Play the scenario. Set the camera target to chaser. The chaser immediately reorients for the first rendezvous maneuver that is performed at about August 6, 2022, 12:27:41 AM UTC. The magenta marker represents the docking port mimicked by the conical sensor.
play(sc); camtarget(v,chaser);
After the first maneuver is complete, the chaser reorients for the second rendezvous maneuver that is performed at about August 6, 2022, 11:40:41 PM UTC.

After the second rendezvous maneuver, the chaser is about 1 km below the target, with a small offset from the target radial position vector, and a relative velocity close to 0 m/s. The error in the position and velocity is the result of the approximation of the impulsive delta-v in the two rendezvous maneuvers.
After rendezvous is complete, the chaser enters the docking phase. It reorients for initial approach attitude. Its translational reaction control thrusters eliminate the lateral offset from the target radial position vector, and it starts closing in on the target at 0.3 m/s.
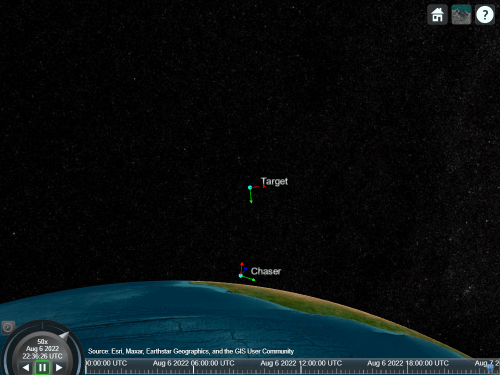
After the distance between the chaser and the target reduces to 100 m, the chaser enters the transposition phase. It reorients to the final docking attitude and maneuvers around target to position itself 20 m in front of the target.
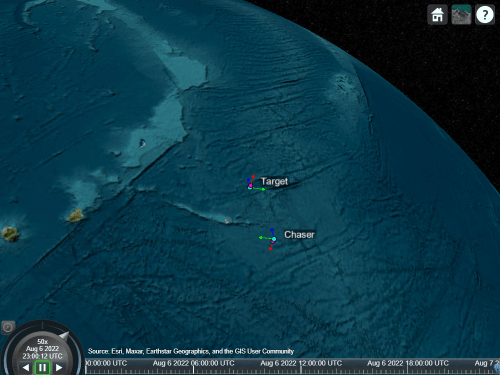
Once transposition is complete, the chaser enters the final approach phase, in which the chaser starts closing in on the target at 0.3 m/s.
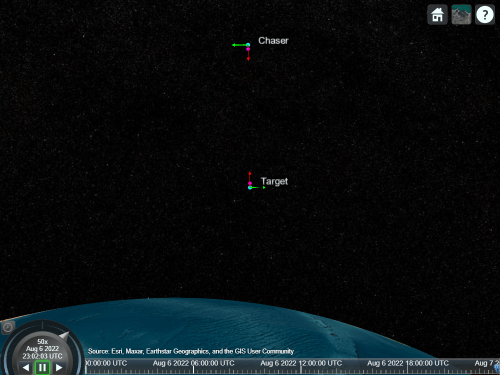
When the range to target reduces to 10 m, the chaser reduces its closing rate to 0.03 m/s.

Docking is complete when the range to target further reduces to 1 m.