Orbit Propagator Kepler (unperturbed)
Propagate orbit of one or more spacecraft using Kepler universal variable formulation

Libraries:
Aerospace Blockset /
Spacecraft /
Spacecraft Dynamics
Alternative Configurations of Orbit Propagator Kepler (unperturbed) Block:
Orbit Propagator Numerical (high precision)
Description
The Orbit Propagator Kepler (unperturbed) block propagates the orbit of one or more spacecraft using the Kepler universal variable formulation. The Orbit Propagator Kepler (unperturbed) and Orbit Propagator Numerical (high precision) blocks are alternative configurations of the same block.
Orbit Propagator Kepler (unperturbed) — Kepler universal variable formulation (quicker)
Orbit Propagator Kepler Numerical (high precision) — More accurate
The Orbit Propagator Kepler (unperturbed) block does not take into account atmospheric drag, third body gravity, or solar radiation pressure. For orbit propagations that take these effects into account, see the Orbit Propagator Numerical (high precision) block.
The size of the provided initial conditions determines the number of spacecraft being modeled. If you supply more than one value for a parameter in the Orbit tab, the block outputs a constellation of satellites. Any parameter with a single provided value is expanded and applied to all the satellites in the constellation. For example, if you provide a single value for all the parameters on the block except True anomaly, which contains six values, the block creates a constellation of six satellites, varying true anomaly only.
The block applies the same expansion behavior to input port A_icrf (applied acceleration). This port accepts either a single value expanded to all spacecraft being modeled, or individual values to apply to each spacecraft.
For more information on the propagation methods the Orbit Propagator blocks use, see Orbit Propagation Methods.
You can define initial orbital states in the Orbit tab as:
A set of orbital elements
Position and velocity state vectors in International Celestial Reference Frame (ICRF) or fixed-frame coordinate systems.
The block uses quaternions, which are defined using the scalar-first convention.
For more information on the coordinate systems the Orbit Propagator blocks use, see Coordinate Systems.
Examples
Constellation Modeling with the Orbit Propagator Block
Propagate the orbits of a constellation of satellites and compute and visualize access intervals between the individual satellites and several ground stations.
Mission Analysis with the Orbit Propagator Block
Compute and visualize line-of-sight access intervals between satellites and a ground station.
Lunar Mission Analysis with the Orbit Propagator Block
Compute and visualize access intervals between the Apollo Command and Service module and a rover on the lunar surface. The module's orbit is modeled using Reference Trajectory #2 from the NASA report Variations of the Lunar Orbital Parameters of the Apollo CSM-Module [2]. This is a lunar orbit studied by NASA for the Apollo program. The example uses:
High Precision Orbit Propagation of the International Space Station
Propagate the order of the International Space Station (ISS) using high precision numerical orbit propagation.
Ports
Output
Position of the spacecraft with respect to (ICRF or fixed-frame), returned as a 3-element vector or numSat-by-3 array, where m is number of spacecraft, at the current time step. The size of the initial conditions provided in the Orbit tab control the port dimension. numSat is the number of spacecraft.
Data Types: double
Velocity of the spacecraft with respect to ICRF or fixed-frame, returned as a 3-element vector or numSat-by-3 array, at the current time step. numSat-by-3 array. The size of the initial conditions provided in the Orbit tab control the port dimension.
Data Types: double
Time at current time step, returned as a:
scalar — If you specify the Start data/time parameter as a Julian date.
6-element vector — If you specify the Start data/time parameter as a Gregorian date with six elements (year, month, day, hours, minutes, seconds).
This value is equal to the Start date/time parameter value + the elapsed simulation time.
Dependencies
To enable this parameter, select the Output current date/time (UTC Julian date) check box.
Data Types: double
Parameters
Main
Orbit propagation method, specified as:
Kepler (unperturbed)— Uses a universal variable formulation of the Kepler problem to determine the spacecraft position and velocity at each time step. This method is faster thanNumerical (high precision).Numerical (high precision)— Determine the spacecraft position and velocity at each time step using numerical integration. This option models central body gravity based on the settings in the Central body tab. This method is more accurate thanKepler (unperturbed), but slower.
Programmatic Use
Block Parameter:
propagator |
| Type: character vector |
Values:
'Kepler (unperturbed)' | 'Numerical (high
precision)' |
Default:
'Kepler (unperturbed)' |
To enable additional external accelerations to be included in the integration of the spacecraft equations of motion, select this check box. Otherwise, clear this check box.
Dependencies
To enable this check box, set Propagation method to
Numerical (high precision).
Programmatic Use
Block Parameter:
accelIn |
| Type: character vector |
Values:
'off' | 'on' |
Default:
'off' |
Input additional accelerations, specified as ICRF or
Fixed-frame. These accelerations are included in
integration of the spacecraft equations of motion.
Dependencies
To enable this parameter:
Set Propagation method to
Numerical (high precision)Select the Input external accelerations check box
Programmatic Use
Block Parameter:
accelFrame |
| Type: character vector |
Values:
'ICRF' | 'Fixed-frame' |
Default:
'ICRF' |
Coordinate frame for output ports, specified as ICRF or
Fixed-frame. These port labels are affected:
Output port X
Output port V
Dependencies
To enable this parameter, set Propagation method to
Numerical (high precision).
Programmatic Use
Block Parameter:
outportFrame |
| Type: character vector |
Values:
'ICRF' | 'Fixed-frame' |
Default:
'ICRF' |
Initial start date and time of simulation, specified as a Julian or Gregorian date. The block defines initial conditions using this value.
Tip
To calculate the Julian date, use the juliandate function.
Programmatic Use
Block Parameter:
startDate |
| Type: character vector |
Values: 'juliandate(2020, 1, 1,
12, 0, 0)' | valid scalar Julian date | valid Gregorian date including
year, month, day, hours, minutes, seconds as 6-element vector |
Default:
'juliandate(2020, 1, 1, 12, 0, 0)' |
To output the current date or time, select this check box. Otherwise, clear this check box.
Programmatic Use
Block Parameter:
dateOut |
| Type: character vector |
Values:
'off' | 'on' |
Default:
'off' |
Out-of-range block behavior, specified as follows:
| Action | Description |
|---|---|
None
| No action. |
Warning
| Warning in the Diagnostic Viewer, model simulation continues. |
Error (default) | Error in the Diagnostic Viewer, model simulation stops. |
Programmatic Use
Block Parameter:
action |
| Type: character vector |
Values: 'None' |
'Warning' | 'Error' |
Default:
'Warning' |
Orbit
Define the initial states of the space craft.
Input method for initial states of orbit, specified as Orbital
elements or ICRF state vector.
Programmatic Use
Block Parameter
stateFormatKep |
| Type: character vector |
Values:
'Orbital elements' | 'ICRF state
vector' |
Default:
'Orbital elements' |
Orbit classification, specified as:
Keplerian— Model elliptical orbits using six standard Keplerian orbital elements.Elliptical equatorial— Define an equatorial orbit, where inclination is 0 or 180 degrees and the right ascension of the ascending node is undefined.Circular— Define a circular orbit, where eccentricity is 0 and the argument of periapsis is undefined.Circular equatorial— Define a circular orbit, where eccentricity is 0 or 10 degrees. Argument of periapsis and the right ascension of the ascending node are undefined.
Dependencies
To enable this parameter, set Initial state format to
Orbital elements.
Programmatic Use
Block Parameter:
orbitType |
| Type: character vector |
Values:
'Keplerian' | 'Elliptical equatorial' |
'Circular inclined' | 'Circular
equatorial' |
Default:
'Keplerian' |
Half of ellipsis major axis, specified as a 1D array whose size is the number of spacecraft.
For parabolic orbits, this block interprets this parameter as the periapsis radius (distance from periapsis to the focus point of orbit).
For hyperbolic orbits, this block interprets this parameter as the distance from periapsis to the hyperbola center.
Dependencies
To enable this parameter, set Initial state format to
Orbital elements.
Programmatic Use
Block Parameter:
semiMajorAxis |
| Type: character vector |
| Values: scalar | 1D array of size m, number of spacecraft |
Default:
'6786000' |
Deviation of the orbit from a perfect circle, specified as a scalar or 1D array of size that is number of spacecraft.
If Orbit type is set to Keplerian,
value can be:
0for circular orbitBetween
0and1for elliptical orbit1for parabolic orbitGreater than
1for hyperbolic orbit
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elements.Orbit type to
KeplerianorElliptical equatorial.
Programmatic Use
Block Parameter:
eccentricity |
| Type: character vector |
Values:
0.01 | scalar | value between 0 and
1, or greater than 1 for Keplerian orbit
type | 1D array of size numSat |
Default:
'0.01' |
Vertical tilt of the ellipse with respect to the reference plane measured at the ascending node, specified as a scalar or 1D array of size numSat, in specified units. numSat is the number of spacecraft.
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elementsOrbit type to
KeplerianorCircular inclined
Programmatic Use
Block Parameter:
inclination |
| Type: character vector |
| Values: 50 | scalar | 1D array of size numSat | degrees between 0 and 180 | radians between 0 and pi |
Default:
'50' |
Right ascension of ascending node (RAAN), specified as a scalar value between
0 and 360 or 1D array of size
numSat, in specified units. numSat is the
number of spacecraft. RAAN is the angular distance along the reference plane from the
ICRF x-axis to the location of the ascending node (the point at
which the spacecraft crosses the reference plane from south to north).
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elements.Orbit type to
KeplerianorCircular inclined.
Programmatic Use
Block Parameter:
raan |
| Type: character vector |
Values:
95 | scalar value between 0 and
360 | 1D array of size m number of
spacecraft |
Default:
'95' |
Angle from the spacecraft ascending node to periapsis (closest point of orbit to the central body), specified as a 1D array of size m that is number of spacecraft, in specified units.
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elementsOrbit type to
Keplerian
Programmatic Use
Block Parameter:
argPeriapsis |
| Type: character vector |
Values:
'95' | scalar value between 0 and
360 | 1D array of size numSat |
Default:
'93' |
Angle between periapsis (closest point of orbit to the central body) and the initial position of spacecraft along its orbit at Start date/time, specified as a scalar or 1D array of size numSat, in specified units. numSat is the number of spacecraft.
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elements.Orbit type to
KeplerianorElliptical inclined.
Programmatic Use
Block Parameter:
trueAnomaly |
| Type: character vector |
Values:
'203' | scalar | degrees between 0 and
360 | radians between 0 and
2*pi | 1D array of size numSat |
Default:
'203' |
Angle between the ascending node and the initial position of spacecraft along its orbit at Start date/time, specified as a scalar or 3-element vector or 1D array of size number of spacecraft, in specified units.
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elements.Orbit Type to
Circular inclined.
Programmatic Use
Block Parameter:
argLat |
| Type: character vector |
Values:
'200' | scalar | degrees between 0 and
360 | radians between 0 and
2*pi | 1D array of size numSat |
Default:
'200' |
Angle between the ICRF x-axis and the eccentricity vector, specified as a scalar or 3-element vector or 1D array of size number of spacecraft, in specified units.
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elements.Orbit type to
Elliptical equatorial.
Programmatic Use
Block Parameter:
lonPeriapsis |
| Type: character vector |
Values: 100 | scalar | degrees between
0 and 360 | radians between
0 and 2*pi | 1D array of size
m, number of spacecraft |
Default:
'100' |
Angle between the ICRF x-axis and the initial position of spacecraft along its orbit at Start date/time, specified as a scalar or 1D array of size numSat, in specified units. numSat is the number of spacecraft.
Dependencies
To enable this parameter, set:
Initial state format to
Orbital elements.Orbit type to
Circular equatorial.
Programmatic Use
Block Parameter:
trueLon |
| Type: character vector |
Values:
'150' | scalar | degrees between 0 and
360 | radians between 0 and
2*pi | 1D array of size numSat |
Default:
'150' |
Cartesian position vector of spacecraft in ICRF coordinate system at Start date/time, specified as a 3-element vector for single spacecraft or numSat-by-3 array for multiple spacecraft. numSat is the number of spacecraft.
Dependencies
To enable this parameter, set Initial state format to
ICRF state vector.
Programmatic Use
Block Parameter:
inertialPosition |
| Type: character vector |
Values:
[3649700.0 3308200.0 -4676600.0] | 3-element vector for single
spacecraft or 2-D array of size m-by-3 array of multiple
spacecraft |
Default:
'[3649700.0 3308200.0 -4676600.0]' |
Cartesian velocity vector of spacecraft in ICRF coordinate system at Start date/time, specified as a 3-element vector for single spacecraft or 2-D array of size m-by-3 array of multiple spacecraft.
Dependencies
To enable this parameter, set Initial state format to
ICRF state vector.
Programmatic Use
Block Parameter:
inertialVelocity |
| Type: character vector |
Values:
[-2750.8 6666.4 2573.4] | 3-element vector for single
spacecraft or 2-D array of size m-by-3 array of multiple
spacecraft |
Default:
'[-2750.8 6666.4 2573.4]' |
Cartesian position vector of spacecraft in fixed-frame coordinate system at Start date/time, specified as a 3-element vector for single spacecraft or 2-D array of size m-by-3 array of multiple spacecraft.
Dependencies
To enable this parameter, set:
Propagation method to
Numerical (high precision).set Initial state format to
Fixed-frame state vector.
Programmatic Use
Block Parameter:
fixedPosition |
| Type: character vector |
Values:
'[-4142689.0 -2676864.7 -4669861.6]' | 3-element vector for
single spacecraft or 2-D array of size m-by-3 array of multiple
spacecraft |
Default:
'[-2750.8 6666.4 2573.4]' |
Cartesian velocity vector of spacecraft in fixed-frame coordinate system at Start date/time, specified as a 3-element vector for single spacecraft or 2-D array of size m-by-3 array of multiple spacecraft.
Dependencies
To enable this parameter, set:
Propagation method to
Numerical (high precision).Initial state format to
Fixed-frame state vector.
Programmatic Use
Block Parameter:
fixedVelocity |
| Type: character vector |
Values:
'[1452.7 -6720.7 2568.1]' | 3-element vector for single
spacecraft or 2-D array of size m-by-3 array of multiple
spacecraft |
Default:
'[1452.7 -6720.7 2568.1]' |
Central Body
Configure the central body environment around which the spacecraft orbits.
Celestial body, specified as Earth,
Moon, Mercury,
Venus, Mars,
Jupiter, Saturn,
Uranus, Neptune,
Sun, or Custom, around which
the spacecraft defined in the Orbit tab orbits.
Programmatic Use
Block Parameter: centralBody |
| Type: character vector |
Values:
'Earth' | 'Moon'
|'Mercury' | 'Venus' |
'Mars' | 'Jupiter' |
'Saturn' | 'Uranus' |
'Neptune' | 'Sun' |
'Custom' | |
Default: 'Earth' |
Units
Parameter and port units, specified as:
| Units | Distance | Velocity | Acceleration | Mass | Area | Density |
|---|---|---|---|---|---|---|
Metric (m/s) | meters | meters/sec | meters/sec2 | Kilograms | m2 | kg/m3, some density outputs 1/m3 |
Metric (km/s) | kilometers | kilometers/sec | kilometers/sec2 | Kilograms | m2 | kg/m3, some density outputs 1/m3 |
Metric (km/h) | kilometers | kilometers/hour | kilometers/hour2 | Kilograms | m2 | kg/m3, some density outputs 1/m3 |
English (ft/s) | feet | feet/sec | feet/sec2 | Slugs | feet2 | lbm/ft3, some density outputs 1/ft3 |
English (kts) | nautical mile | knots | knots/sec | Slugs | feet2 | lbm/ft3, some density outputs 1/ft3 |
Programmatic Use
Block Parameter:
units |
| Type: character vector |
Values:
'Metric (m/s)' | 'Metric (km/s)' |
'Metric (km/h)' | 'English (ft/s)' |
'English (kts)' |
Default:
'Metric (m/s)' |
Parameter and port units for angles, specified as
Degrees or Radians.
Programmatic Use
Block Parameter:
angleUnits |
| Type: character vector |
Values:
'Degrees' | 'Radians' |
Default:
'Degrees' |
Time format for Start date/time (UTC Julian date) and output
port tutc, specified as
Julian date or Gregorian.
Programmatic Use
Block Parameter:
timeFormat |
| Type: character vector |
Values:
'Julian date' | 'Gregorian' |
Default:
'Julian date' |
Alternative Configurations
The Orbit Propagator
Numerical (high precision) block propagates the orbit of one or more
spacecraft by a numerical (high precision) propagation method. To enable this block, set
Propagation method to Numerical (high
precision).
Libraries:
Aerospace Blockset /
Spacecraft /
Spacecraft Dynamics
Algorithms
The Orbit Propagator Kepler (unperturbed) block works in the ICRF and fixed-frame coordinate systems:
ICRF — International Celestial Reference Frame (ICRF). This frame can be treated as equal to the ECI coordinate system realized at J2000 (Jan 1 2000 12:00:00 TT. For more information, see ECI Coordinates).
To describe a point in space, you need a frame of reference that does not rotate with respect to the stars. The ICRF, with the origin at the center of the Earth and orthogonal vectors I, J, and K, is used as the frame of reference. The fundamental plane is the IJ-plane, which is closely aligned with the equator with a small offset that changes over time because of precession and nutation of the rotation axis of the Earth.
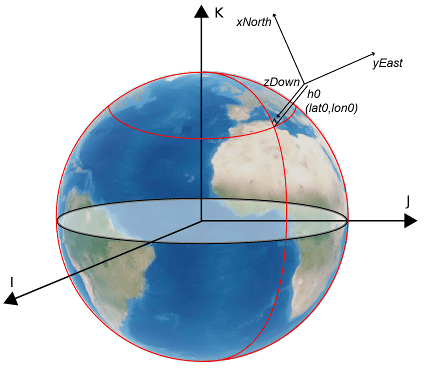
Fixed-frame — Fixed-frame is a generic term for the coordinate system that is fixed to the central body (its axes rotate with the central body and are not fixed in inertial space). For high precision orbit propagation methods
When the central body is earth, and the Earth orientation parameters (EOPs) are used, the Fixed-frame for Earth is the International Terrestrial Reference Frame (ITRF). This reference frame is realized by the IAU2000/2006 reduction from the ICRF coordinate system using the earth orientation parameter file provided. If Earth orientation parameters are not used, the block still uses the IAU2000/2006 reduction, but with Earth orientation parameters set to
0.When the central body is moon, and the moon libration angles are provided as input, the fixed-frame coordinate system for the moon is the Mean Earth/pole axis frame (ME). This frame is realized by two transformations. First, the values in the ICRF frame are transformed into the Principal Axis system (PA), the axis defined by the libration angles provided as inputs to the block. For more information, see Moon Libration. The states are then transformed into the ME system using a fixed rotation from the "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006" [5]. If the Moon libration angles input is not provided, the fixed frame is defined by the directions of the poles of rotation and prime meridians defined in the "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006" [5].
When the Central Body is custom, the fixed-frame coordinate system is defined by the poles of rotation and prime meridian defined by the block input α, δ, W, or the spin axis properties.
In all other cases, the fixed frame for each central body is defined by the directions of the poles of rotation and prime meridians defined in the "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006" [5].
The Aerospace Blockset™ supports two top-level orbit propagation methods:
Kepler (unperturbed) and Numerical (high
precision).
For more information, see Orbit Propagation Methods.
References
[1] Vallado, David. Fundamentals of Astrodynamics and Applications, 4th ed. Hawthorne, CA: Microcosm Press, 2013.
[2] Gottlieb, R. G., "Fast Gravity, Gravity Partials, Normalized Gravity, Gravity Gradient Torque and Magnetic Field: Derivation, Code and Data," Technical Report NASA Contractor Report 188243, NASA Lyndon B. Johnson Space Center, Houston, Texas, February 1993.
[3] Konopliv, A. S., S. W. Asmar, E. Carranza, W. L. Sjogen, D. N. Yuan., "Recent Gravity Models as a Result of the Lunar Prospector Mission, Icarus", Vol. 150, no. 1, pp 1–18, 2001.
[4] Lemoine, F. G., D. E. Smith, D.D. Rowlands, M.T. Zuber, G. A. Neumann, and D. S. Chinn, "An improved solution of the gravity field of Mars (GMM-2B) from Mars Global Surveyor", Journal Of Geophysical Research, Vol. 106, No. E10, pp 23359-23376, October 25, 2001.
[5] Seidelmann, P.K., Archinal, B.A., A’hearn, M.F. et al. "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006." Celestial Mech Dyn Astr 98, 155–180 (2007).
[6] Montenbruck, Oliver, and Gill Eberhard. Satellite Orbits: Models, Methods, and Applications. Springer, 2000.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2020bThe Orbit Propagator block has been updated to take into account:
The effects of third body gravity on orbit propagation.
Space weather data from a data file generated by the
aeroReadSpaceWeatherDatafunction.Solar radiation pressure (SRP).
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)