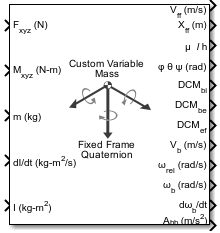
Custom Variable Mass 6DOF ECEF (Quaternion)
Implement quaternion representation of six-degrees-of-freedom equations of motion of custom variable mass in Earth-centered Earth-fixed (ECEF) coordinates
Libraries:
Aerospace Blockset /
Equations of Motion /
6DOF
Description
The Custom Variable Mass 6DOF ECEF (Quaternion) block implements a quaternion representation of six-degrees-of-freedom equations of motion of custom variable mass in Earth-centered Earth-fixed (ECEF) coordinates. It considers the rotation of a Earth-centered Earth-fixed (ECEF) coordinate frame (XECEF, YECEF, ZECEF) about an Earth-centered inertial (ECI) reference frame (XECI, YECI, ZECI). The origin of the ECEF coordinate frame is the center of the Earth. For more information on the ECEF coordinate frame, see Algorithms.
Aerospace Blockset™ uses quaternions that are defined using the scalar-first convention.
Limitations
This implementation assumes that the applied forces act at the center of gravity of the body.
This implementation generates a geodetic latitude that lies between ±90 degrees, and longitude that lies between ±180 degrees. Additionally, the MSL altitude is approximate.
The Earth is assumed to be ellipsoidal. By setting flattening to 0.0, a spherical planet can be achieved. The Earth's precession, nutation, and polar motion are neglected. The celestial longitude of Greenwich is Greenwich Mean Sidereal Time (GMST) and provides a rough approximation to the sidereal time.
The implementation of the ECEF coordinate system assumes that the origin is at the center of the planet, the x-axis intersects the Greenwich meridian and the equator, the z-axis is the mean spin axis of the planet, positive to the north, and the y-axis completes the right-handed system.
The implementation of the ECI coordinate system assumes that the origin is at the center of the planet, the x-axis is the continuation of the line from the center of the Earth toward the vernal equinox, the z-axis points in the direction of the mean equatorial plane's north pole, positive to the north, and the y-axis completes the right-handed system.
Ports
Input
Output
Parameters
Algorithms
The origin of the ECEF coordinate frame is the center of the Earth. In addition, the body of interest is assumed to be rigid, an assumption that eliminates the need to consider the forces acting between individual elements of mass. The representation of the rotation of ECEF frame from ECI frame is simplified to consider only the constant rotation of the ellipsoid Earth (ωe) including an initial celestial longitude (LG(0)).

The translational motion of the ECEF coordinate frame is given below, where the applied forces [Fx Fy Fz]T are in the body frame. Vreb is the relative velocity in the wind axes at which the mass flow () is ejected or added to the body in body-fixed axes.
where the change of position in ECEF is calculated by
and the velocity of the body with respect to ECEF frame, expressed in body frame , angular rates of the body with respect to ECI frame, expressed in body frame . Earth rotation rate , and relative angular rates of the body with respect to north-east-down (NED) frame, expressed in body frame are defined as
The rotational dynamics of the body defined in body-fixed frame are given below, where the applied moments are [L M N]T, and the inertia tensor I is with respect to the origin O.
The rate of change of the inertia tensor is defined by the following equation.
The integration of the rate of change of the quaternion vector is given below.
References
[1] Stevens, Brian, and Frank Lewis. Aircraft Control and Simulation, 2nd ed. Hoboken, NJ: John Wiley & Sons, 2003.
[2] McFarland, Richard E. "A Standard Kinematic Model for Flight at NASA-Ames." NASA CR-2497.
[3] "Supplement to Department of Defense World Geodetic System 1984 Technical Report: Part I - Methods, Techniques and Data Used in WGS84 Development" DMA TR8350.2-A.
Extended Capabilities
Version History
Introduced in R2006aSee Also
6DOF (Euler Angles) | 6DOF (Quaternion) | 6DOF ECEF (Quaternion) | 6DOF Wind (Quaternion) | 6DOF Wind (Wind Angles) | Custom Variable Mass 6DOF (Euler Angles) | Custom Variable Mass 6DOF (Quaternion) | Custom Variable Mass 6DOF Wind (Quaternion) | Custom Variable Mass 6DOF Wind (Wind Angles) | Simple Variable Mass 6DOF ECEF (Quaternion) | Simple Variable Mass 6DOF (Euler Angles) | Simple Variable Mass 6DOF (Quaternion) | Simple Variable Mass 6DOF Wind (Wind Angles)